コンテンツ
www.ncbi.nlm.nih.gov/labs/pmc/articles/PMC3284140/
2011年8月17日オンライン公開
Troy Day
概要
進化の多様化のプロセスは、潜在的な結果が存在する広大な遺伝子型空間で展開される。過去1世紀の間に、この多様化に関する理論の発展は目覚しく、理論の成功は、その適用範囲にかかっている。
このような理論の多くは、主に歴史的または現代的なパターンに基づいて選択された、潜在的な遺伝子型の空間の比較的小さなサブセットに焦点を当て、この事前に定義されたセット内での進化のダイナミクスを予測している。
このようなアプローチは、進化の多様性の潜在的な開放性を説明するような、より広い視点に押し上げることができるのだろうか?これまでにも、この分野では多くの重要な理論的発展があったが、このような理論をどこまで推し進めることができるのかという疑問は解決されなかった。
ここでは、遺伝のデジタルな性質のために、このようなアプローチを使って答えられる質問の種類には本質的な限界があることを示す定理が証明されている。特に、非常に単純な進化システムにおいても、進化が進歩的でない限り、進化の潜在的なオープンエンド性を考慮した完全な理論は達成できないのである。この定理は、ゲーデルの不完全性定理や、計算可能性理論の切断問題と密接な関係がある。
キーワード:進化の予測、計算可能性、論理学の哲学、進歩的進化、進化論、数理生物学
1. 序論
進化論の多くは、重要な意味で、基本的に歴史的なものである。進化の多様化のプロセスは、潜在的な結果の広大な遺伝子型空間で展開され、この空間のある部分を探索し、他の部分を探索しない。それにもかかわらず、現在の理論の多くは、主に歴史的または現代的なパターンに基づいて選択された、この空間の比較的小さなサブセットに注目し、進化のダイナミクスを予測している。この方法は、短期的な予測には有効であるが、進化によってこの定義済みのセットの外側に真の意味で新しい遺伝子型が生まれると、最終的には失敗することになる [1]。
多くの進化モデルの予測能力におけるこの潜在的な限界は,進化論の発展を通じて様々な場面で指摘されてきた [1-4]。最も有名なのは,オランダの生物学者ヒューゴ・デフリースが「自然淘汰は適者生存を説明できるが,適者の到来を説明することはできない」と発言したことであろう [5]。このような発言は,進化のモデルの多くが,進化の木の非常に小さな(局所的な)領域に注目しているという意味で,「局所的」あるいは「閉鎖的」と呼ばれるものであり,進化がオープンエンドなプロセスである可能性を説明していないという考え方を示唆している。
進化の「クローズド」モデルと「オープンエンド」モデルの違いについては、後ほど詳しく説明するが、近年、分析の境界を押し広げて、自然にオープンエンドモデルと呼ばれるようになりつつある興味深い研究がいくつか発表されている。これらの研究には、抽象的なレプリケーター集団のモデル[3,6-9]、進化の可能性の空間を探索するモデル[10-12]、進化の遷移の分析[13,14]、進化中の対立遺伝子の効果の分布を予測するモデル[15-18]、進化可能性の研究[4]などがある。同様に,進化の一般的な特性,創発的な特性を探求するin silicoや人工生命の実験も数多く行われている[3,19-27]。一般的に、これらの分析は、よりオープンエンドな進化を許容すると、より豊かな進化の可能性が生まれることを示している。
これらの研究を総合すると,理論的にオープンエンドの進化を考慮することで,興味深い新知見が得られ,また,新たな検証可能な予測が得られることが示唆される[15-18]。とはいえ、オープンエンドの進化を考慮した理論的な研究はまだ比較的少ないので、このように進化論をさらに広げることで、まだ多くのことが学べると期待される。したがって、この記事の目的は2つある。まず、進化のオープンエンドモデルとクローズドモデル(以下に詳しく定義する)には重要な違いがあるという事実を強調し、オープンエンドモデルの方が進化の過程をより忠実に表現しているのではないかということを示唆したいのである。第二に、より重要なことは、進化の潜在的なオープンエンド性を受け入れた予測理論への推進が、閉鎖的な進化モデルが直面している以上の、さらなる障害に直面する可能性があるかどうかを検討したいということである。別の言い方をすれば、「予測可能なオープンエンドの進化論の開発はどの程度まで可能なのか」という質問である。
上記の質問に完全な答えを出すことはできないが、以下では少なくとも部分的な答えを提示する。さらに、この答えが、計算可能性理論の切断問題や、数理論理学のゲーデルの不完全性定理と興味深い関係にあることを示す。特に、これらの分野の結果を用いて、プログレッシブ・エボリューションの概念と、このような予測可能なオープンエンドの理論を発展させる可能性とを正式に結びつける定理を証明する。進化が進行するかどうか、またいつ進行するかについては、依然として議論があり[28-30]、この議論の一部は、進行の正確かつ一般的な定義がないことに起因している。したがって,今回の結果を別の見方をすれば,そのような定義を提供していることになる。この点については,§4でより詳しく説明する。
2. 動機となる例
これらのやや抽象的なアイデアに焦点を当てるために、進化予測に関わる具体的な動機付けの例から始める価値がある。このセクションでは、主に関連する広範な概念的問題に焦点を当てて、そのようにする。そして、では、これらの問題をより具体的に取り上げる。
進化論を用いてヒトインフルエンザの動態を予測することを考えてみよう。具体的には、「1918年に発生したスペイン風邪のようなパンデミックが再び起こる可能性はあるか」という問いに答えようとする。これは明らかに難しい質問であり、まだ定義が曖昧なので、さらに絞り込んで考えてみよう。このような予測ができるかどうか懐疑的になる理由の1つは、初期条件やパラメータ値の不確実性や、関係する進化プロセスの不確実性にある。言い換えれば、予測に必要な情報がすべて揃っていないということである。さらに、予想外の事態が発生すると、正確な予測ができなくなることもある。例えば、予期しない火山の噴火により、民間の航空旅行のパターンが一時的に変化し、それによってインフルエンザの疫学的・進化的動態が変化する可能性がある。
このような現実的な限界が重要であることは明らかであるが、正確な進化予測を行う上での障害はそれだけなのであろうか、それとも他にも「固有の」限界があるのであろうか。進化の予測が難しいのは、単に進化のプロセスについての知識がないからなのか、それとも、原理的にもそのような進化の予測ができない理由があるのか。
この記事の焦点は最後の質問であり、したがって、少なくとも一時的には、上記の実用的な懸念を脇に置くことにする。具体的には、関連するすべての進化プロセスを適切に捉えるモデルを構築し、そのようなモデルを使用するために必要なすべてのパラメータ推定値を得ることができると仮定しよう。詳細は省くが、まず最初に決めなければならないのは、モデルに関連するひずみ空間である。最も単純なシナリオでは、2つの菌株(例えば、1918年の菌株と現在の優勢な菌株)のみを考慮する。もっと洗練されたシナリオでは、ダイナミクスに重要であると考えられる複数の株が含まれるかもしれない。いずれにしても、結果として得られるモデルは、有限の(そして比較的小さな)数の株にのみ焦点を当てているので、§1で述べた意味での「閉じた」モデルとなる。さらに、ある時点で感染する可能性のある人の数が離散的で有限であることを考えると、可能な進化の結果の数も有限(かつ比較的少ない)である。後で詳しく説明するが、このことは、プロセスが定常状態に達するか、周期的な挙動を示すことを意味する(付録E参照)。したがって、もしクローズドモデルが進化の過程を正確に記述しているのであれば、原理的には、これら2つの結果のいずれかが発生するまでモデルを実行するだけで、上記の質問に答えることができる。その時点で、モデルの実行中に1918年のスペイン風邪のパンデミックが発生したかどうか(あるいは有意な確率で発生したかどうか)を観察すればよいのである。
しかし、進化の過程がオープンエンドであったらどうであろうか。この可能性を探るには、「オープンエンド」の意味をより具体的に説明する必要がある。インフルエンザを例に考えてみよう。A型インフルエンザのゲノムサイズは12,000以上のヌクレオチドであり、そのため可能な遺伝子型の数は膨大である。どのくらいの数の遺伝子型が可能なのかを理解するために、インフルエンザの8つのゲノムセグメントのうち、最も小さいセグメントだけに注目してみよう。この場合、約800ヌクレオチドしかないので、約4800種類の遺伝子型が考えられる。これは、宇宙に存在する原子の数の約10^400倍に相当する。モデルがオープンエンドであるためには、このような膨大な数の進化の結果を許容しなければならない。そうすれば、現実と同じように、進化の変化が止まることなく続き、本質的に無限に新しい結果を生み出すことができる。これを理論的に理解するための最も単純な方法は、可能な遺伝子型の空間が無限であると仮定することである。
このように考えると、進化論が終わりのない進化の過程を捉えようとするならば、その状態空間は実質的に無限でなければならないことになる。これは必要なことであるが、終わりのない進化の十分な条件ではない。例えば、集団遺伝学における確率的マルコフモデルの多くは、無限の状態空間を持っているが(例えば、無限対立遺伝子モデル[31])それにもかかわらず、オープンエンドの進化を示すことはない。むしろ、マルコフ連鎖が不可分で正の再帰性を持つという仮定など、さらなる仮定がなされることが多い。これらの仮定は主に数学的な利便性のために行われるが、単一のユニークな均衡または定常分布の存在を保証することになるため、オープンエンドの進化の可能性は排除される。その結果、このようなモデルでは、進化の変化が無限に続く可能性を捉えることができない。
では、これらの仮定を緩和して、本当に無限の進化を可能にする理論を開発したらどうであろうか。その場合、進化の予測にはさらに問題があるのであろうか?例えば、冒頭の「インフルエンザの進化」という問いに答えることは難しくなるであろうか。少なくとも、進化の過程が平衡あるいは定常的な分布に落ち着くことが保証されていないため、上記のクローズドモデルのアプローチではもはや十分ではない。したがって、我々が期待できるのは、モデルの構造を使って、そのような結果が起こるかどうかを証明する方法があるということである。このように、進化を予測することの現実的な難しさはさておき、インフルエンザの進化について上記のような疑問に答えられるかどうかは、原理的にも明らかではない。
このような問題は、現在、計算可能性や数理論理学の分野で大きく取り上げられ始めており、大雑把に言うと、インフルエンザの進化に関する上記のような問いに答えられる理論を「否定完全理論」と呼んでいる。これは、ある文が真であるか、あるいはその形式的な否定が真であるかを判断できるという意味で、理論が完全であるという考え方を反映した用語である。例えば、インフルエンザの文脈では、否定完全理論は、「スペイン風邪は再び起こる」という文が真であるか、それとも「スペイン風邪が再び起こるということは真ではない」という形式的否定が真であるかを予測することができる。より一般的には、否定完全な進化論とは、遺伝子型空間のうち、進化によって探索される部分とそうでない部分を決定できるようなものである。
このような否定完全進化論は、オープンエンドの進化を認めれば可能なのだろうか?本稿の残りの部分では、この質問に対する答えが、漸進的進化の考え方と密接に関連していることを示する。特に、進化のシステムが、その遺伝子組成が世代ごとにどのように変化するかについて、すべてを理解できるほど単純であったとしても、次のことが証明されるのである。
進化の過程が進歩的である場合にのみ、否定完全進化論が可能である。
このことは、DNAが進化にデジタルな継承のメカニズムを提供していることに起因している。Maynard Smith & Szathmáry [13]が指摘しているように、組み合わせの複雑性が生じることで、進化は事実上、オープンエンドになる。実際、後述するように、デジタル継承によって、進化(すなわち、集団の遺伝的組成の変化)を自然数上の力学系として特徴づけることができる。したがって、以下に証明される定理は、進化をモデル化するためのものだけでなく、そのような力学系のすべてに成り立つ。その結果、この定理は、ゲーデルの不完全性定理[32-35]や、計算可能性理論の切断問題[36,37]など、数学やコンピュータサイエンスの他の結果と密接に関連している。
3. 定理の記述と証明
上の記述に正確さを与えるためには、「進化の過程」が何を意味するのか、また進化論が否定完全であることが何を意味するのかを明示しなければならない。その目的は、極めて単純な進化の過程においても、進化論に何らかの固有の制限があるかどうかを判断することである。
この目的のために、単純化された進化の過程を考えてみよう。そこでは、ある最大の集団サイズを持つ複製子の十分に混合された集団があり、各複製子には一片のDNAが含まれている。この遺伝コードは、構成と長さの両方で変異することができ、あらかじめ制限はない。各複製子は、集団の現在の遺伝的組成にのみ依存する方法で生存し、繁殖するとする。さらに簡単にするために、世代は離散的であるとする。イベントが連続時間で発生しても、すべての結論は成立する(付録E)。最後に、説明を簡単にするために、本文では通常、進化のダイナミクスは決定論的であると仮定する。繰り返しになるが、すべての結果は、いくつかの追加の仮定があるものの、確率的な進化のダイナミクスの場合に一般化される(付録E)。
上記の進化力学では、システムの遺伝子組成は時間とともに進化し、各タイプの複製者の数(例えば、インフルエンザの各可能な遺伝子型による感染の数)によって、いつでもシステムの状態を特徴づけることができる。目標は、進化の多様化の過程で、潜在的な進化の結果の空間のどの部分が探索され、どの部分が探索されないかを予測できる進化論を構築できるかどうかを判断することである。形式的には、以下に示す結果は、派生する文が再帰的に列挙可能なあらゆる理論に対して有効である。公理的な理論はその一例であるが、(大雑把に言えば)原理的にコンピュータで実装可能なあらゆる理論的アプローチがこのカテゴリーに入る(付録A)。実際、この定理の記述と証明は、計算可能性理論のいくつかのアイデアに依存している(付録B)。
DNAのデジタルな性質は、原理的に、可能な複製者の種類の数が離散的で拘束されていないことを意味し、Maynard Smith & Szathmáry [13]は「不定型」遺伝と呼んでいる。不定形の遺伝は、無限の進化を可能にする。その結果、原理的には、進化中の可能な人口状態の集合は正の整数に同型であり、すなわち、可能な人口状態の集合と正の整数の間には一対一対応が存在する。このような集合は列挙可能と呼ばれ、実際、人口状態の集合は、計算可能な意味で実質的に列挙可能である(付録C)。したがって、可能なすべての人口状態に、ユニークな整数値の「コード」を効果的に割り当てることができる。
もちろん、実際には、必要な化学的構成要素のプールが有限であるという理由だけで、可能なレプリケーターの種類の数には制限がある。しかし、前述したように、不定形遺伝の組み合わせ的な性質は、可能な集団状態の実際の数が事実上無限であることを意味している。説明を簡単にするために、本文では可能な集団状態の集合が本当に無限であることを仮定しているが、付録Fでは「効果的に無限」という概念を正確にし、この場合の類似結果を提供している。
以上のコード化により、進化を数学的に正の整数からそれ自身へのマッピングとして形式化することができる。例えば、決定論的なケースでは、次の時間ステップにおける各遺伝子型の個体数を、現在の数の関数として教えてくれるモデル(例えば、マッピングF)から始めることができる。そして、上記のコード化の下で、E(n)が時間nにおける人口の状態(正式にはその整数コード番号)を示す場合、モデルは、ある関数Gについて、ある初期条件とともに、1変数の整数のマッピングE(n + 1) = G(E(n))として再構成することができる。同様に、確率的な場合、確率的なマッピングFから始めれば、マッピングE(n + 1) = H(E(n))として再構成することができる。ここで、Hは、次の時間ステップにおけるコード番号のセットに対する確率分布を、現在の分布の関数として与える(そして、Eは整数上の確率のベクトルです)。したがって、一般的には、進化の軌跡は、単に整数値の引数を持つ整数値の関数であると見なすことができる。もちろん、母集団の状態をコード化する方法が異なれば、異なるマップ、GまたはHに対応し、したがって、異なる関数E(n)になる。また、GやHの領域は正の整数のすべてである必要はなく、実際には、異なる初期条件によって異なる領域が生じる可能性があることにも注意してほしい。これは、進化の過程で異なる引力の流域が存在することに対応する。
また、進化のマッピング(すなわちGまたはH)は、集団の現在の遺伝子組成のみの関数であると仮定したが、この仮定を緩和し、進化の変化が環境の他の側面にも依存することを認めることができることも注目に値する。具体的には、「集団の状態」の定義を拡大して、遺伝子の状態と、遺伝子が存在する環境に関連する他の変数の状態の両方を含めることができる。繰り返しになるが、このような一般化された過程を自然数上の力学系として捉え直すことができる限り、ここで紹介した結果はすべて有効である。
以上の議論は、進化を自然数上の力学系として捉えることができることを示しており、また、オープンエンドの進化という概念を公式化することができるようになった。決定論的な設定では、マッピングGが前に訪れた状態を決して再訪しない場合、進化はオープンエンドとなる。同様に、確率的な設定では、写像Hが正の確率で各世代において常に少なくとも1つの新しい状態を認める場合、進化はオープンエンドになる。
進化を自然数上の力学系と見なすことができるので、進化論は自然数を操作し、自然数に関する記述を推論するための特定の規則のセットと見なすことができる。計算可能性理論は、正の整数を自分自身にマッピングする関数を扱うので、問題を分析するための自然なツールのセットを提供する。関数を有限回のステップで評価するためのアルゴリズムが存在する場合,その関数は「計算可能」と呼ばれる(付録B).
ここでも決定論的なケースに注目すると,ある時間ステップから次の時間ステップまでの人口の状態を予測できるという仮定のもとでは,関数E(n)は計算可能である(付録B参照).さらに,すべての計算可能な関数の集合は,列挙可能である[37].したがって、k番目のそのような関数をφk(n)と表すと、進化プロセス、E(n)はこのセットのメンバーに対応しなければならないことは明らかである。この特定のメンバーをφE(n)と表し、特定の集団の状態を識別するために使用される整数のコーディングを変更すると、異なる関数が得られることに再度注意してほしい。
であり、したがって、集合であるAn external file that holds a picture, illustration, etc.の異なるメンバーである。
図1 人口状態の符号化、および定理の模式図
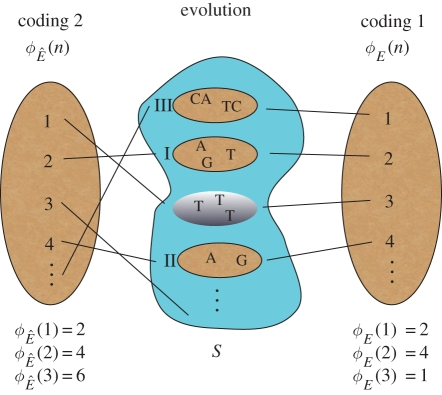
真ん中の不規則な形は人口状態の空間Sを表しており、4つの状態が描かれている(楕円形)。ローマ数字は、進化の過程で各状態が訪れる時間を示している(銀色の斜線の状態s = {T,T,T}は、一度も訪れない)。右と左の縦の楕円は、正の整数による2つの異なるコード化を、それぞれの進化的マッピング、φE(n)と で、最初の3つの時間ステップに渡っている。例えば、状態’T,T,T’は、そのコード(すなわち’1′)を見つけることによって決定することができ、その後、マップ、写真やイラストなどを保持する外部ファイルを繰り返する。
で、最初の3つの時間ステップに渡っている。例えば、状態’T,T,T’は、そのコード(すなわち’1′)を見つけることによって決定することができ、その後、マップ、写真やイラストなどを保持する外部ファイルを繰り返する。 で、’1’より大きい出力が得られるまで(タイムステップ1で発生するため)。
で、’1’より大きい出力が得られるまで(タイムステップ1で発生するため)。 )。)
)。)
この時点でまだ’1’が訪れていなければ、今後も訪れることはない。逆に、すべての集団状態が決定可能であるならば、符号化1の下で、定理の証明のパート2で提供されるアルゴリズムを適用して符号化2を得ることができ、それによって進化が進歩的であることが証明されることになる。
進化の過程では、ある集団の状態が時間の経過とともに訪れる(確率的な場合、ある時点で発生する確率がしきい値よりも大きい場合、状態が訪れたとみなする;付録E)。これらは「進化的に達成可能な」状態と呼ばれる。我々の形式論では、これは関数φE(n)がnの増加に伴い、その範囲REの様々な値を取ることに対応する(図1)。否定完全な進化論とは、あるコードxがx∈REを満たすか、それとも代わりにx∉REを満たすかを判断できるものである。計算可能性理論の言葉で言えば、これは「x∈RE」という述語が決定可能かどうかを問うことに相当する(付録B;[37])。先ほどのインフルエンザの例で言えば、1918年型のパンデミックに対応する人口状態をxとすると、「スペイン風邪は再び起こる」という文は、数論的な文x∈REに対応する。同様に、「スペイン風邪が再び起こることは真実ではない」という文は、数論的な文x ∉ REに対応する。
最後に、進歩的な進化の正確な定義を与えることができる。直感的には、進化の時間とともに増加する人口の定量化可能な特性がある場合、進化は進行性である。上記の形式化に関して、これは、コード番号が進化中に増加するように、母集団の状態を再コード化する方法があることを意味する。正式に は、進化過程の対応する記述がすべてのnを
は、進化過程の対応する記述がすべてのnを 満たすように、正の整数による母集団状態の計算可能な1対1のコーディングが存在する場合、進化は進行性である。繰り返しになるが、前に示したインフルエンザの例に関して、進化が進行性である場合、先験的に何らかの方法がある
満たすように、正の整数による母集団状態の計算可能な1対1のコーディングが存在する場合、進化は進行性である。繰り返しになるが、前に示したインフルエンザの例に関して、進化が進行性である場合、先験的に何らかの方法がある インフルエンザの発生が発生すると、母集団のコード番号が増加するように母集団の状態をコード化する(この進行の定義については、§4で詳しく説明する)。
インフルエンザの発生が発生すると、母集団のコード番号が増加するように母集団の状態をコード化する(この進行の定義については、§4で詳しく説明する)。
これで、正確で技術的な言語の観点から定理を述べることができる。
再び、先ほどのインフルエンザの例で言えば、もし進化が進行性であれば、インフルエンザの進化に伴って、母集団のコード番号が増加するように、母集団の状態を先験的にコード化する方法があるはずである(この進行性の定義については、§4で詳しく説明する)。
これで、正確で専門的な言葉で定理を述べることができる。
Theorem 3.1.
「X ∈ R Eは」あれば決定可能であり、かつ、正の整数で人口状態の符号化、計算、一対一が存在する場合にのみ、 そのような進化の過程の対応する記述こと、
そのような進化の過程の対応する記述こと、 を満たす
を満たす  全てのために 、N。
全てのために 、N。
証明(図1,詳細は付録BとDを参照)。
その1:コーディングが存在する場合
コードが存在する場合 、そのようなことは
、そのようなことは すべてのためにN、述語「X ∈ R Eは、」決定可能である。
すべてのためにN、述語「X ∈ R Eは、」決定可能である。
仮説により 、進化過程の対応する記述について、
、進化過程の対応する記述について、 すべてのnについて、計算可能な全単射が存在する。任意の集団状態のために、xは、元の符号化に、聞かせて
すべてのnについて、計算可能な全単射が存在する。任意の集団状態のために、xは、元の符号化に、聞かせて 全単射下に対応するコードである
全単射下に対応するコードである 、と定義
、と定義 ここで、μは、I(Hが(私は))が最小値を示し、I引数のためのHは、(I()が真であると付録B)。さらに、R k(n)= { x:ϕ k(i)= xを定義する。、I ≤ N }(即ち範囲φ k個(nはステップによって訪問)、N、付録B)。明らかに、 ‘
ここで、μは、I(Hが(私は))が最小値を示し、I引数のためのHは、(I()が真であると付録B)。さらに、R k(n)= { x:ϕ k(i)= xを定義する。、I ≤ N }(即ち範囲φ k個(nはステップによって訪問)、N、付録B)。明らかに、 ‘  ‘は
‘は 有限であり、列挙できる
有限であり、列挙できる ため、さらには進化の進歩的な性質のために決定可能である。したがって、 ‘
ため、さらには進化の進歩的な性質のために決定可能である。したがって、 ‘  ‘も決定可能である。最後に、Sを使用して、進化的に達成可能な一連の人口状態を示する。我々はそれを持ってい
‘も決定可能である。最後に、Sを使用して、進化的に達成可能な一連の人口状態を示する。我々はそれを持ってい ます。定義上、、
ます。定義上、、 を取得することに注意してほしい
を取得することに注意してほしい 。したがって、 ‘ X ∈ R Eは、 ‘も決定可能である。
。したがって、 ‘ X ∈ R Eは、 ‘も決定可能である。
パート2:場合述語「のx ∈ R Eは」次いでコードが存在する決定可能である ように、
ように、 すべてのためのn。
すべてのためのn。
次のように、人口状態と適切なコーディングの間に必要な計算可能な全単射を構築できる。まず、人口状態の効果的なコーディングを行う。仮説によって「X ∈ R Eは、」決定可能であるため、我々は、人口の状態を経て進むことができ、Xを、次のアルゴリズムを適用し、昇順に、:
- もしX ∉ R E、Kそれまでのような状態番目、使用kは、その新たなコードとして奇数番目。
- もしX ∈ R E、計算μ I(φ E(I)= X)、および使用私に、その新たなコードとして番目の偶数。
したがって、 は偶数のセットであり、進化が進むにつれて昇順でアクセスされる。特に、
は偶数のセットであり、進化が進むにつれて昇順でアクセスされる。特に、 ポイント(i)および(ii)で説明した上記のマッピングを示すために使用する。ここで、C -1は、xを生成したコーディングの逆マッピングである(つまり、コードxを取り、対応する母集団の状態sを返する)。あり
ポイント(i)および(ii)で説明した上記のマッピングを示すために使用する。ここで、C -1は、xを生成したコーディングの逆マッピングである(つまり、コードxを取り、対応する母集団の状態sを返する)。あり ます。最後の等式は、
ます。最後の等式は、 状態ϕ E(n + 1)が発生する時間を決定し(n + 1)、この値の2倍に等しい新しいコードを割り当てるという事実に基づいている(上記のポイント(ii))。したがって、
状態ϕ E(n + 1)が発生する時間を決定し(n + 1)、この値の2倍に等しい新しいコードを割り当てるという事実に基づいている(上記のポイント(ii))。したがって、 。▪▪
。▪▪
4. 考察
この論文には2つの主な目標がある。1つ目の目的は、進化のオープンエンドモデルとクローズドモデルの違いを強調し、オープンエンドモデルの方が実際の進化プロセスをよく捉えている可能性を示唆することである。第2の目的は、予測可能なオープンエンドの進化論の開発がどの程度可能かを探ることである。上記の定理は、この問題と、計算可能性理論や数理論理学からの分析との間に、興味深い関連性があることを示している。また、この定理は、そのような理論がどの程度可能であるかということと、Progressive evolutionの概念との間に、形式的なつながりを示している。
この定理は、否定完全理論の発展の可能性と漸進的進化との間の等価関係を述べているので、2つの異なる方法で読むことができる。まず、「進化が進行しているならば、否定完全説も可能である」というものである。これは、意外と知られていないことかもしれない。進化が進行性であるならば、その過程には、理論を構築する際に利用できるような、かなりの規則性があるはずである。この定理の2つ目の読み方は、「逆暗示」という観点からのものである。これは少し意外で、もし進化が進歩的でなければ、否定完全な理論は不可能である、というものである。
これらの結果は、デジタル継承によって進化がオープンエンドになるという事実に基づいている[13]。代わりに、遺伝システムが有限数の離散的な型しか許さないとしたら、進化は周期的な振る舞いを示すか、(確率的な揺らぎを伴うかもしれないが)平衡状態に達するだろう。このような場合、原理的には、起こりうるすべての進化的結果の有限リストを作成すればよいので、進化の否定完全理論は些細なことであるが可能である(前述のインフルエンザの例で説明したように)。
もちろん、デジタル継承があるにもかかわらず、さまざまな理由で可能な集団状態の数には限界があると考えられる。しかし、デジタル継承の組み合わせ的な性質から、可能な集団状態の数は事実上無限大と考えられる。このような場合には、無限という概念を、実質的に無限という正確な概念に置き換えることで、類似の定理を証明することができる(付録F)。同様に、本文の主な結果は進化が決定論的であることを前提としているが、進化過程の本質的な確率的性質を考慮した類似の定理が成り立つ(付録E)。
進化の進行という概念はやや曖昧であり、一般的に合意された進行の正確な定義は存在しない。その結果、進行性の進化がどの程度起こるのかについて意見の相違が生じている[28,29]。プログレッシブ・エボリューションのアイデアを完全に議論することは、この記事の範囲を超えているが、ここではいくつかのポイントがある。
進歩的進化の議論のほとんどは、平均フィットネス、フィットネス、複雑性、その他の比較的目につきやすい生物学的測定値などの量を含んでいる。このような議論の多くは、進化のパターンを見つけようとするときに歴史的なパターンを見るという意味で、遡及的でもある。しかし、このような進歩の議論には問題がある。第一に、方向性を持って変化する集団の明らかな、そして生物学的に意味のある特性を容易に特定することができればよいのだが、現在のところすべての可能性を考慮しているとは考えられない。したがって、進行を定義する際には、生物学的に興味深い、しかしまだ発見されていない量が時間とともに増加する可能性を残しつつ、非常に一般的な方法で定義することが望ましいと思われる。第二に、進行の定義を歴史的なパターンに求めることは、基本的にデータを見て、それに合う仮説を設計することである。進歩は、過去に遡るのではなく、将来に向かって定義されるべきであり、それは予測価値を持つべきであることを意味する。もし進化が進歩的であれば、先験的に増加する量を定義できるはずである。
ここで使われている進行の定義は、上記の難点に対処するために意図的に選ばれたものである。したがって、現状では、必ずしも特定の生物学的測定値とは結びついていない。ここで使用されている定義では、時間とともに増加する可能性のある量は、進化の進行において果たす役割以外に、明白な生物学的解釈を持つ必要はない。このレベルの一般性は、それが何であるかについて必ずしも具体的なことを何も知らずに、そのような量の存在について質問している場合には望ましいと思われる。しかし、このような一般性は、もしこの意味で進化が進歩的であるならば、進歩的な形質は、先験的に自然な生物の生物学的属性には必ずしも対応しない、集団の非常に複雑な特性である可能性があることを意味する。このように、ここで紹介する定理は、理論の限界を示すものではなく、進歩的進化の定義として捉えたい読者もいるだろう。言い換えれば、否定完全な進化論を原理的に構築することができる進化過程として、漸進的進化を定義することができるかもしれない。そしてこの定理は、この定義が、進化の時間とともに増加する何らかの量が存在することと等価であることを示している。
ここで紹介したような決定可能性の結果は、しばしば誤った解釈をされがちである[38]。そのため、上記の定理が何を言っているのか、また何を言っていないのかを明確にすることが重要だ。まず、この定理は、進化の予測理論の開発が不可能であることを意味するものではない。現在の進化生物学の研究の大部分は、そのような予測能力の開発に向けられており、したがって、定理はそのような理論の存在を出発点としている。その理論的根拠は、現在の研究の発展をこの方向に押し進めることに成功したとしても、答えられる質問の種類に、他の固有の制限があるかどうかを判断することにある。この定理は、そのような固有の限界があることを示している。要するに、この問題は、進化が進まない場所を予測することの難しさから生じているのである。言い換えれば、予測理論は常に進化の道筋を描くのに使えるが、面白いことに、進化が進まない道筋を描くのには使えないのである。ここで紹介する定理は、事実上、進化が進歩的でない限り、後者を行うことは不可能であることを示している。
これらの考察は、先に述べたインフルエンザの進化のような例の文脈ではどのように解釈されるのであろうか。まず、その例ですでに述べたように、分析は基本的にベストケースのシナリオを取ることから始まる。システムに関する十分な知識があり、次の時間ステップにおけるインフルエンザ集団の遺伝子構成を、現在の構成の関数として(おそらく確率的な方法で)完全に予測するオープンエンドモデルを開発したと仮定する。そして、「1918年型のインフルエンザ・パンデミックが再び起こる可能性はかなり高いのか?上の定理は、たとえそのような完璧なモデルがあったとしても、インフルエンザの進化が進行性でない限り、この種の質問には答えられないことを示している。言い換えれば、進化の過程でインフルエンザ集団の何らかの特性が方向性を持って変化しない限り(例えば、抗原性プロファイルの何らかの側面が方向性を持って変化するなど)このような予測はできないということになる。さらに、完璧なモデルを使ってインフルエンザの進化の過程を時系列にマッピングすることができても、それだけでは、インフルエンザが探索しない遺伝子型空間の部分をマッピングすることはできないため、このような制限が生じる。
上記の制限は、集団の遺伝的進化に関する予測に適用されるが、表現型の予測にのみ関心がある場合はどうであろうか。例えば、どの株がパンデミックを起こすかに関わらず、1918年と同じような深刻なインフルエンザのパンデミックが再び起こるかどうかを予測することができるだろうか。同様に、抗ウイルス剤への耐性が進化するかどうかを、その遺伝的背景に関わらず予測することができるだろうか。もし、遺伝子型と表現型の対応が一対一であれば、表現型の進化を予測することは、遺伝子型の進化を予測することと変わらないことになる。しかし、多くの異なる遺伝子型が同じ表現型を生み出すことができるとしても、表現型の進化を予測するには、進化の過程で遺伝子型空間のある部分が訪れるかどうかを予測する必要がある。そのため、このような場合には、前述のすべての制限が適用される。唯一の例外は、遺伝子型-表現型マップの結果、遺伝子型空間の次元が事実上無限であっても、表現型空間の次元が有限である場合である。しかし、この場合でも、ある時間ステップから次の時間ステップへの集団の状態を予測するには、表現型の知識だけで十分である場合(つまり、進化を理解するために遺伝子の状態を考慮する必要がない場合)には、上記の予測の限界が適用される。これは、興味のあるいくつかの表現型では可能かもしれないが、すべての表現型で可能であるとは思えない。
しかし、表現型の進化のパターンの中には、非常に予測しやすいものがあると言えるかもしれない。例えば、集団に薬物の圧力をかけると、その薬物に対する耐性が進化するのは必然であると考えられる。このような知見と今回の結果をどのように整合させればよいのだろうか。まず、抵抗性の進化はある程度予測できるように見えるが、帰納的予測と演繹的予測を区別する必要がある。我々が薬剤耐性の進化を自信をもって予測できるのは、それが繰り返し起こっているのを目の当たりにしているからである。したがって、帰納的な議論によって、再び起こることが予想される。このような帰納的予測は、統計モデルから得られる予測をデータの範囲を超えて外挿することと概念的には似ている。一方、演繹的予測は、基礎となる一連の原理や機械的プロセスから予測を導き出すことで行われる。ある意味で、帰納的予測は対象となる現象の理解を必要としないのに対し、演繹的予測は、物事がどのように機能するかについての基礎的なモデルに基づいている。ここで紹介する結果は、あくまでも演繹的予測に適用されるものである。
しかし、薬剤耐性のようなものの進化に関する第二の可能性は、(少なくともこの「ローカル」スケールでは)進化が進行しているということである。例えば、抗ウイルス剤の圧力がかかった状態でインフルエンザの進化がどのように進むかについて正確な基礎モデルを策定した場合、進化の過程で方向性を持って変化する何らかの集団レベルの量が存在することは十分に考えられる。実際、このような方向性があるからこそ、このようなケースでも進化を予測できると確信できるのではないであろうか。ただし、進化に方向性がないとしても、ここで紹介した定理は、いくつかの予測ができる可能性を否定するものではないことに注意する必要がある。例えば、薬剤耐性の進化について否定完全予測を行う理論が開発される可能性は十分にある。この定理は、進化の過程が進歩的でない限り、進化の任意の側面について否定的完全予測を行うことはできないということを示している。
すでに述べたように、ここで紹介したすべての結果は、ある時間ステップから次の時間ステップへの進化を予測する理論を開発できるという前提で始まっている。現在の理論的アプローチがこれを実現するところまで押し進めることができるかどうかは、別の、そして未解決の問題である。興味のある進化システムが非常に単純でない限り、そうするにはかなりの障害があるのは確かである[39]。歴史的偶発性の問題に加えて、天気予報のような初期条件の不確実性の役割は、長期的な予測を妨げる可能性がある(ただし、確率的な記述は可能かもしれない)。これは依然として重要かつ活発な研究分野であり、ここで紹介する定理はその観点を提供するものではない。むしろ、そのような理論が開発されたとしても、進化が進んでいない限り、答えられる質問の種類には本質的な制限があることを明らかにしているだけである。
進化が進行性でない限り、関心のある進化のプロセス全体に対する否定完全理論は不可能であるが、短期的・局所的な予測のために、完全に受け入れられる否定完全理論が開発される可能性も排除していない。実際、計算可能性理論や数理論理学に同様の固有の制限があったとしても、人々がこれらの研究分野で驚くべき進歩を遂げることができなかったのと同様に、進化生物学の場合も同様である。§1で述べたように、潜在的な進化の結果の空間のサブセットに注目することで、すでに多くの理論的進歩が得られている。進化の過程がどのようなものであっても、考える空間を広げることで、この方向での理論的発展を推し進めていくことは可能である。しかし、この定理は、進化が進歩的でない限り、このような発展をすべて否定完全な進化予測を導き出す単一の統一された原理に包含することは不可能であることを示唆している。
進化がどの程度の方向性を示すかについては、文献にいくつかの先行する理論的な結果があり、今回の結果がこれらの先行研究とどのように関連しているかを検討することは有益である。例えば、かなり一般的な進化の確率モデルを用いて、「自由フィットネス」と呼ばれる量が進化の過程で常に非減少することが示されている[40]。しかし、この分析では、状態空間が有限であると仮定され、使用されたマルコフモデルが(暗黙のうちに)正のリカレントであると仮定されていたため、オープンエンドの進化は認められなかった。その結果、ユニークな定常分布が存在し、継続的な進化が妨げられたのである。
しかし、このような分析[40]では、真にオープンエンドな進化は認められていないが、状態空間が十分に大きく、過渡的なダイナミクスが十分に長ければ、事実上オープンエンドなモデルであると合理的に主張できるかもしれない。このように、自由なフィットネスに関する結果はまだ適用されるべきではないであろうか?言い換えれば、進化の過程で増加する何らかの量(自由フィットネス)が存在することを示唆しており、したがって否定完全理論が可能であることを示唆しているのではないであろうか?答えはノーであり、その理由は微妙だが重要である。岩佐[40]の研究における自由フィットネスの定義は、進化の過程で方向性を変えることが示唆されている他の量[30]と同様に、エントロピーと密接に関連する尺度に基づいている。重要なことは、これらのエントロピーの尺度と集団の状態との間のマッピングは一対一ではないということである。なぜならば、同じエントロピーの値(あるいは同じ「自由なフィットネス」の値)を持つ生物学的に異なる集団の状態が多数(実際には無限に多い可能性がある)存在するからである。その結果、進化の過程で自由フィットネスのような指標が減少しなくても、自由フィットネスに変化がなくても、生物学的に興味深く重要な進化の変化が無限に起こり得るのである。大雑把に言えば、エントロピーのような指標は、方向性が変わるかもしれない興味深い物理量を提供するが、エントロピーと生物学的に興味深い量との関係は単純である必要はない。
同様に、生物進化は熱力学の第二法則に従う物理システムの中で行われるので、一般的な尺度であるエントロピーは、最終的にシステムに方向性を与えるものでなければならないと主張する人もいるかもしれない。繰り返しになるが、これはシステム全体としては正しいのであるが、エントロピーと生物学的に関心のある集団の状態との間のマッピングは一対一ではない。したがって、物理システム全体のエントロピーは常に増加しなければならないが、構成要素(例えば、関心のある生物学的部分)のエントロピーはこのように変化する必要はない。
このような考察は、進化の過程をどのように研究するか、あるいは現在の理論研究をどのように行うかについて、どのような意味を持つのであろうか。進化生物学者は、このような結果を気にする必要があるのであろうか?例えば、この結果は、理論をより良くするための新しいアイデアを示しているのだろうか?この質問に対する答えはひとつではないが、この点に関しては、2つのポイントがある。まず、オープンモデルとクローズドモデルの区別は、進化のモデルを分類するのに便利な方法であるが、現在はあまり評価されていないようである。特に、オープンエンドモデルは、クローズドモデルでは対応できない、新しい、そして潜在的に非常に重要な進化上の問題を問うのに適していることを考えると、進化論の新しい方向性を示唆している[3,10,11,19-24]。第二に、オープンエンドの進化プロセスに対する理論の開発に関心があるならば、ここで紹介する定理は、そのような理論の予測能力をどこまで高めることができるかについて、固有の「上限」があることを明らかにする。特に、このような理論は、新しい進化の問いかけへの扉を開くものであるが、進化が進歩的でない限り、答えの出ない問いかけが残ることになる。さらに、この定理を、進化が進行性であることを証明する手段として(つまり、否定完全な理論を開発することによって)使うことや、完全な進化論が可能であることを証明するために(つまり、進化が進行性であると判断することによって)使うことは、おそらく難しいであろうが、それでも、この結果は、これらの2つの重要な、そしてやや異なる生物学的な考えが、基本的には同じものであることを明らかにしている。
ここで紹介する定理は、自然数の公理論に対するゲーデルの不完全性定理と密接な関係がある[32-35,41]。公理的な理論は、シンボルのセット、論理装置(例えば述語微積分)シンボルを含む公理のセット、シンボルを含む新しいステートメントを導き出すことができる演繹のルールのセット(「定理」と呼ばれる)から構成される[41]。このようなシステムがあれば、推論のルールをアルゴリズム的に繰り返し適用することで、定理を導き出すことができる。
1900年代初頭には、自然数を表現するためのこのような公理的理論を作り出そうとする協調的な試みが行われた。しかし,ゲーデルの不完全性定理[32-35,41]は,単純な数論的記述ができるような十分に豊かな公理系では,このようなことは不可能であることを明らかにした。例えば、公理系が「x∈RE」という述語に対応する数論的な文を表現できるほど豊かであれば、すべての真の数論的な文を生成し、偽の数論的な文を生成することはできないことを示している[41]。なぜなら、もしそれができるならば、「x∈RE」または「x∉RE」のどちらかに対応する数論的な文を常に定理として作り出すことができるからである。しかし、これができるということは、述語’x∈RE’を決定するためのアルゴリズム的な手順を提供していることになるが、ここで紹介した結果が示すように、これは必ずしも可能ではないことがわかっている。
計算可能性理論からのハルティング問題[36,37]も、ここで紹介した結果と密接に関連している。すでに説明したように、ある集団の状態が進化的に達成可能かどうかという問題は、与えられた正の整数が特定の計算可能な関数の範囲内にあるかどうかという問題と同等である。さらに、この最後の問題は、与えられた整数が計算可能な関数の領域内にあるかどうか(すなわち、特定の整数の入力が与えられたときに、その関数が有限時間で値を返すかどうか)という類似の問題に直接つながっている。最後の問題は正確にはハルティング問題であり,任意の計算可能な関数に対するハルティング問題を解く一般的なアルゴリズム手順は存在しないことが知られている[36,37].
先に述べたように、非常に一般的な意味で、ここで紹介した結果は、離散的な可能性の無限セット上のマルコフ力学系によって忠実に記述できるあらゆるシステム(すなわち、オープンエンドの力学系)に適用可能である。したがって、今回の結果には、進化そのものに特有のものがあるのではないかと疑問に思うかもしれない。ある意味では、答えは「ノー」である。しかし、このような数学的抽象化の力は、プロセスの根本的な重要構造を明らかにすることにある。進化は、遺伝が不確定である限り、オープンエンドの力学系であり、そのようなオープンエンドの力学系である他のすべてのプロセスと基本的な共通点を持っている。
しかし同時に、この結果は進化にとって特別な意味を持っている。このようなオープンエンドの力学系であるという性質を意味のある形で共有している興味あるプロセスは、おそらく他にはほとんどないであろう。例えば、非常に多くの興味あるプロセスは、潜在的な結果の空間が比較的小さいため、明らかにオープンエンドではない。さらに、オープンエンドである可能性のあるプロセスでは、すべての可能な結果を区別することは理論的にあまり興味がないことがあり、したがって、関連する結果の空間は依然として比較的小さいことがある。さらに、興味のある結果の空間が本当にオープンエンドである場合でも、一部のプロセス(例えば、一部の物理プロセス)は、そのような否定完全予測が容易にできるほど単純なダイナミクスを持っている(つまり、ここで考えられている意味でシステムは「進歩的」である)。このように、定理によって詳述されている制限は、主に、進行の問題が未解決であるような、開放的で複雑なプロセスにおいて興味深いものである(付録D)。不定形遺伝の下での進化は、この2つの基準を満たす、ややユニークなプロセスかもしれない。
しかし、このような決定可能性の結果が興味を引くプロセスは他にもあるであろう。結局のところ、重要な意味で、生物学的進化は、物理学や化学の創発的特性に他ならないのである。実際、このような理論上の制限については、特に物理学におけるいわゆる万物の理論に関連して、以前から議論されてきた[43]。この問題に関する一般的なコンセンサスはまだ得られていないと言っていいであろう[38]。しかし、ここで紹介する定理は、進化現象を説明することを目的としたあらゆる物理学や化学の理論に影響を与える。ここで提示された定理は,進化現象を説明しようとするあらゆる物理的・化学的理論に示唆を与えている。
謝辞
N. H. Barton, G. Bell, S. A. Frank, S. Gandon, A. Gardner, S. Gavrilets, B. Glymour, M. Hochberg, L. Nagel, S. P. Otto, S. Proulx, A. Read, A. Rosales, P. Taylor, M. Turelli, and the Queen’s Math Bio Groupには、刺激的な会話や原稿へのフィードバックをいただき、結果を明確にし、見通しを立てるのに大いに役立った。本研究は、NSERC Canada Discovery Grant、E.W.R. Steacie Fellowship、Canada Research Chairs Programmeの支援を受けて行われた。
付録 A. 理論
「理論」という言葉は、技術的な意味で使われている。理論は,理論の言語を構成するシンボルのセット,与えられたものとみなされる前提条件のセット,および推論のルールのセットから構成される[41]。記号は現実のある構成要素を表し、前提条件は記号の解釈を通じて現実についての記述を構成するものである。そして、推論のルールは、言語のシンボルに関する新たなステートメントを推論するための有効な方法を構成し、したがって、解釈を通じて、現実に関する新たなステートメントを構成する。このように、このような理論では、いくつかの前提条件を取り、推論のルールを適用することで、文が導き出される。
推論のルールを使った一連の演繹的な議論によって導き出されたステートメントは、理論の定理と呼ばれる。本文中の結果は、定理が再帰的に列挙可能な進化論(付録B)つまり、定理が有限の(しかし大きな可能性のある)機械的またはアルゴリズム的なステップ(例えば、推論のルールで定められているように)を使用して導出できる理論であれば、すべて有効である。このことは、コンピュータが機械的にルールに従う以外のことをしないように、計算に基づいたあらゆる理論に明らかに当てはまる[37]。また、機械的な推論のルールを公理に適用するだけで定理が導かれるような公理主義的な理論にも当てはまる[41]。
進化生物学における現在の定量的理論の多くは、上記のテンプレートに当てはまる。例えば、現在の理論では、対立遺伝子の頻度や集団の大きさといったものに形式的な記号を割り当てることで、現実を数学的に抽象化していることが多い。そして、遺伝子型の適合性がどのようにして決まるのかという仮説を形式化するなど、一連の前提条件を設定する。
次に、「推論のルール」を有限回適用して(例えば、ある種の数学的操作を適用して)この理論の形式的記号に関する記述を導き出す。最後に、これらの記号的な記述は、生物学的な意味の観点から再び解釈され、それゆえに進化に関する予測がなされる(図2)。
図2 進化という生物学的プロセスと理論との関係を示す模式図
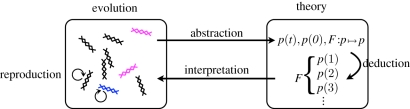
与えられた例では、古典的な集団遺伝学的理論を説明している。進化の要素を表現するために形式的なシステムが作られる(例:p(t)は時刻tにおける青色の遺伝子型の数を表す)。一連の前提条件が指定される(例えば、初期の遺伝子型の数、遺伝子型の適合度がどのように決定されるかなど、これはマッピングFによって具現化される)。続いて、演繹のルールに従う(例えば、マッピングFを繰り返し適用する)ことで、形式理論の要素(例えば、p(1);p(2);p(3)など)に関する新たな記述が得られる。これらの新しい要素は、進化の観点から解釈される(例えば、将来の遺伝子型数の予測など)。
付録B. 計算可能性理論からのいくつかの結果
関数は,有限のステップ数で無制限レジスタマシン(URM)によって評価できるならば,計算可能である[37].Church-Turing thesisは、機械的な手順で評価されると見なすことができるあらゆる関数は、URMによって評価することができると述べている[37]。したがって、Church-Turing論文を考慮すると、何かが計算可能であるかどうかを確認する最も簡単な方法は、有限の(しかし非常に大きな可能性のある)ステップ数で、出力が保証されるような方法でそれを行うようにコンピュータをプログラムできるかどうかを検討することである。
定義 B.1. 関数は,すべての自然数に対して計算可能であれば,全関数である.
定義B.2. 関数は,自然数のある(空ではない)部分集合に対してのみ計算可能であれば,部分関数である.
定義B.3. 集合と自然数との間に双対が存在する場合,その集合は列挙可能である。
定義B.4. この双対とその逆数が計算可能であれば,その集合は効果的に列挙可能である.
定義B.5. 自然数の集合であるAの特性関数は
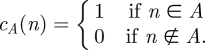
定義B.6. 述語’n∈A’は,その特性関数が計算可能であれば,決定可能である。
定義B.7. 集合Aは,述語’n∈A’がdecidableであれば,再帰的である。
定義B.8. 自然数の集合Aの部分特性関数は
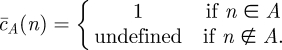
定義B.9. 述語’n∈A’は,その部分特性関数がn∈Aについて計算可能であれば,部分的に決定可能である。
定義B.10. 集合Aは、述語’n∈A’が部分的に決定可能であれば、再帰的に列挙可能である(r.e.と表記する)。
なお、すべての再帰的集合はr.e.であるが、その逆はない。さらに、集合Aは、Aとその補集合Acの両方がr.e.である場合に限り、再帰的である。最後に、任意の有限数の集合は再帰的であることに注意してほしい[37]。
次のような概念や表記法も役に立つであろう。
まず、計算可能な関数は、一連のステップを経て評価できるので、cAo(n)を、評価の第1ステップ後のcA(n)の値と定義することができる。特に,cAo(n)は,次のステップまでに値を返さなかった場合,「null」と評価される.
次に、計算可能性理論の標準的な結果として、ℕ+とℕ+×ℕ+の間に計算可能なバイジェクションが存在することを示している[37]。この写像をB : n ↦ (T1(n), T2(n))とする。
第3に、計算可能性理論では「unbounded search」という概念が中心になっている。特に、「f(y)=kとなる最小のyの値」を表すために、μy(f(y)=k)という表記を使うのが標準的である。
第4に、計算可能性理論の基本的な定理により、すべての計算可能な関数の集合は列挙可能であることが示されている[37]。したがって,k番目の計算可能な関数をφk(n)で表し,その範囲と領域をそれぞれRkとDkで表すことができる.また、Rk(n) = {x : ϕk(i) = x,i ≤ n}という表記を用いる。言い換えれば、もしφk(n)がnの値の増加に対して評価されるならば、Rk(n)はステップnによって訪問されたφk(n)の範囲のサブセットである。これは、φk(n)がトータルであるならば、任意のnに対して明らかに計算可能である。
最後に、進化の過程に対応するマッピングGが計算可能であることが暗黙のうちに仮定されており、したがってE(n)は計算可能な関数であることに注意してほしい。このように、進化の過程は重要な意味で計算に他ならないのである。ほとんどの進化系についてこの仮定を検証したり反論したりすることは現実的ではないが、この仮定が妥当であると期待するには非常に良い理由がある。第一に、生物システムで起こっているプロセスを純粋に「機械的」なものと見なしても構わないのであれば、Church-Turing Thesisに訴えて、Gはそれによって計算可能でなければならないと主張することができる。第二に、プロセスとしての「進化」という言葉の使用は、例えば炭素系の生命体で起こるような、特定のプロセスの具体化に限定されるべきではない。例えば、in silicoの進化で起こるプロセスは、生物学的な進化で起こるプロセスと基本的には同じであると考えられる十分な理由がある。そのため、計算可能であることは明らかである。最後に、生物進化が形式的には計算可能ではない(つまり機械的ではない)場合でも、通常は計算を使ってモデル化できると仮定して作業を進める。
付録C. 人口状態のセットは効果的に列挙可能である
ここでは、可能な人口状態の集合が効果的に列挙可能であること、すなわち、人口状態と正の整数との間に、計算可能な逆数を持つ計算可能な双対が存在することを証明する。このような集合は effectively denumerable とも呼ばれる。
証明 母集団の状態を正の整数に符号化したり復号化したりするための効果的な手順(すなわち、計算可能な手順)を示すだけでよい。最大可能な人口サイズをMとする(正の整数)。M個の「スロット」のそれぞれは、空きがあるか、DNA配列によって完全に特徴づけられる個体によって埋められる。さらに、A=0,C=1,G=2,T=3とした上で、DNA配列をその5′から3′の端まで読み取ることで、集団の各スロットの特徴を一意に定めることができる。
(A)符号化:M個のスロットのそれぞれについて、以下のように数字のコードを計算する。DNAをその5′から3′の端まで読み、n番目の塩基について、n番目の素数を取り、それを上記のようにこの塩基に対応するべき乗に上げる。これらの数字をすべて掛け合わせます。このようにして、それぞれのDNA配列に固有の番号が与えられるので、写像は注入的になる。さらに、2以上の正の整数はすべて一意の素因数分解を持つので、そのような整数はすべてDNA配列に対応している。したがって、「空っぽ」という状態を数字の1でコード化すると、この写像も射影性を持つことになる。さらに、この手順は、どんなDNAに対しても計算可能である。このことから、各スロットには計算可能な符号化があることがわかる。また、母集団は単に有限個のスロットの組合わせであるため、母集団の状態にも計算可能な符号化があることになる。特に、各スロットの符号化は、ℕ+ × …× ℕ+ (ここでℕ+はM回現れる)の中で、その添字で一意に特定できる点を探する。そして、次のように可能なすべての添字を循環させることができる。つまり、合計が1になるすべての添字から始めて、次に合計が2になる添字、などである。これは計算可能であり、各インスタンスには単純に昇順でコード番号を割り当てる。
(B)復号化:任意のコード番号に対して、上記のようにインデックスのセットを循環させ、コード番号に到達した時点で停止し、それらのインデックスを決定する。これらの指数が得られれば、その素因数分解によって対応するDNAを決定することができる。 ▪
付録D 定理に関する追加の技術情報
本文の定理は、’x∈RE’が決定不可能になることが決してないのであれば、ほとんど興味を惹かれないだろう。このような述語が決定不可能な計算可能な関数が存在することは、計算可能性理論ではよく知られているが([37];付録D)ここで考えている進化過程は、特殊な種類の計算可能な関数を表している。特に、それはすべてのnに対してマッピングφk(n + 1) = G(φk(n))を満たさなければならず、ここでG()は適切なドメインを持つ計算可能関数である。この関係を満たす計算可能な関数のサブセットは、Markov, total, computable functionsと呼ばれる。
本節では、一連の3つの公理を示し、これらを合わせて、「x∈RE」が決定不可能なマルコフ計算可能関数が実際に存在することを示す([37,41]も参照)。このような場合、進化的に達成可能な状態の集合REは、「再帰的に列挙可能」と呼ばれることになる(r.e.; なぜなら、マルコフ計算可能な関数について、’x∈RE’は常に少なくとも部分的に決定可能だから)。一方、’x∈RE’がdecidableであれば、REは「再帰的」であると言われる(付録B、D)。
Lemma D.1. ある数の集合が再帰的に列挙可能であるのは、それがある総ての計算可能な関数の範囲である場合に限られる。註:「全」という条件を緩和してもあまり変化はない。
証明 (i) A r.e. ⇒ 「Aは総ての計算可能な関数の範囲である」。
Aがr.e.であることを考えると、Aの部分特性関数は計算可能、すなわち

は計算可能である。ここで、まずa∈Aを選ぶ。これは、双射B : n ↦ (T1(n), T2(n))を使って単純に評価できるので、計算可能な演算である。 写真やイラストなどを格納した外部ファイル。
rsif20110479-i33.jpgを1の値を返すまでnを増やしていき、対応する値T1(n)を特定する。
次に、計算可能な関数を定義する。

そして、再び計算可能な双対性B : n ↦ (T1(n), T2(n))を用いて、f(n) = g(T1(n), T2(n))を定義する。これは、範囲がAに等しい全計算可能な関数である。
(ii) 「Rkは全計算可能関数の範囲である」 ⇒ Rk r.e.
全関数φk(n)を考える。すると、Rkに対する計算可能な部分特性関数を次のように構成することができる。任意の入力値xに対して、μi(φk(i)=x)を評価した後、値1を出力する。 ▪
レムマD.1が与えられれば、次の第2のレムマを証明することができる。
レムマD.2。範囲がr.e.であるが再帰的ではない全計算可能な関数が存在する。
レムマD.1を用いて、r.e.であるがその補集合がr.e.ではない集合が存在することを証明することで、レムマD.2を証明することができる。
証明のスケッチ (by construction; Smith [41] 参照). K = {n : n∈Rn} がそのような集合の一つであることを証明する。したがって、他のそのような集合も構築できることは明らかである。
まず、Kcがr.e.でないことは、カントールの対角線論法を用いて証明することができる(例えば[41])。特に、すべてのr.e.集合は、ある計算可能な関数の範囲であり、また、計算可能な関数は数え切れないので、すべてのr.e.集合の集合は数え切れない。つまり、このリストにない集合を作ればいいのである。n ∉ Rnとなるような数nを選ぶとこの性質を満たすことになり、これがまさにKcである。
あとは、Kがr.e.であることを示せばよいのである。特性関数と同様に、すべての計算可能な関数は、入力ごとに一連の操作を経て評価されるので、任意の計算可能な関数の第1の操作を考えることができる。そこで、次のように定義する。

これが計算可能関数である。
次に、双射B : n ↦ (T1(n), T2(n)) を用いて、f(z,n) = g(T1(z), T2(z),n) を定義する。これも計算可能で、任意のnとzに対して、n + 1か、さもなければRnの要素を出力する。任意の入力値nに対して、μz(f(z,n)=n)を評価した後、値1を出力することで、Kの計算可能な部分特性関数を次のように構成することができる。 ▪
これらの結果は、範囲が再帰的ではなくr.e.である計算可能な関数が存在することを示している。なお、このような関数の中には、領域内の複数の値に対して同じ出力値を持つものがあるかもしれないが、これはMarkov計算可能な関数ではない。理由は単純で、マッピングGは、REが無限である場合、φE(n)がnの増加に伴ってそれ自身を繰り返すことができないことを保証するからである(lemma D.1 and appendix E参照)。したがって、マルコフ計算可能な関数に限定しても、そのような関数の中には再帰的ではないr.e.範囲を持つものがあることを証明する必要がある。これは3つ目のレンマで行う。
レムマD.3. r.e.であるが再帰的ではない範囲を持つすべての全計算可能な関数に対して、同じ範囲を持つ全計算可能なマルコフ関数が存在する。
証拠。ϕ k(n)が合計であり、再帰的ではない再範囲を持っていると仮定する(したがって、R kは無限大です)。計算関数を定義し 、ここで、Z(N)= μ I(φ K(I)∉ R K(N – 1))。あることは明らかである
、ここで、Z(N)= μ I(φ K(I)∉ R K(N – 1))。あることは明らかである 範囲の合計、計算関数であるRのK。ここで、いくつかの計算可能なG()の
範囲の合計、計算関数であるRのK。ここで、いくつかの計算可能なG()の すべてのnについてそれを示す必要がある。構築により、計算可能関数が
すべてのnについてそれを示す必要がある。構築により、計算可能関数が そのドメインがある作品は、RのK。この関数は状態yを取り、この状態が発生する一意の時間を見つけて(つまり、これ
そのドメインがある作品は、RのK。この関数は状態yを取り、この状態が発生する一意の時間を見つけて(つまり、これ は計算可能です)、1を加算する。結果の値は関数で使用さ
は計算可能です)、1を加算する。結果の値は関数で使用さ れ、次のタイムステップで状態を計算する。特に、それを見ることができる
れ、次のタイムステップで状態を計算する。特に、それを見ることができる 。▪▪
。▪▪
付録E. 連続時間と確率論
説明を簡単にするために、本文のすべての結果は、進化の過程が決定論的であり、世代が離散的であることを仮定している。ここでは、これらの制限を緩和すると、類似の定理が成り立つことを示す。
まず始めに、世代が離散的であるという仮定が重要でないことは簡単にわかる。特に、世代が連続的であると仮定すると、どの瞬間にも単一のイベント(例えば、個人の誕生や死亡)しか起こりえないと考えることができる。このように、状態空間が離散的であることから、連続時間プロセスを、離散的なイベントが一様な間隔でなくてもよい時点で発生するものと見なすことができる。
確率を考慮するにはさらに工夫が必要である。このケースの分析では、進化のマッピングGとその初期条件だけでなく、このマッピングの解であるφE(n)についても完全な知識を持っていると仮定した(そして、それは計算可能な全関数です)。
進化の過程を何度も繰り返すと、特定の状態が他の状態よりも頻繁に発生する可能性があるという意味で、これらのいくつかは他の状態よりも可能性が高いかもしれない。決定論的な場合と同様に、ここではMarkov仮定をしている。つまり、任意の時間nにおける集団の状態に関する確率分布は、前の時間n – 1における集団の状態にのみ依存する。言い換えれば、現在の人口状態から次の時間帯の人口状態に関する確率分布への何らかのマッピング、Hが存在する。この写像の解(初期条件が与えられている)は、各時点での状態に関する確率分布を与える。
決定論的な場合と同様に、我々はこの進化過程の解を次のような意味で完全に知っていると仮定する:任意の時間nにおいて、正の支持を持つその時点での状態の集合を簡単に教えてくれる計算可能な関数がある。このように、我々は、全体的で計算可能な、集合値を持つ関数を持っている。
rsif20110479-i41.jpgで、時間nにおける「実現可能な」状態の集合を与える。「チルダ」は、この関数が整数値ではなく集合値の関数になったことを示している。また、否定完全理論の目的は、任意の状態が実現可能な状態のセットに含まれるかどうかを決定することである。
この定式化に対する一つの反論は、すべての状態が、たとえそれが消えてしまうほど小さくても、ゼロではない確率を持っていることを期待してしまうことである。そのため、この定義では、すべての状態が実現可能であると考えられる。この反論に対しては、少なくとも2つの可能性がある。第一に、進化の多くのモデルが、すべての状態がゼロでない確率を持つと仮定しているのは事実であるが(例えば、異なる対立遺伝子が無限に存在するものを含む、突然変異と選択のバランスの多くの確率モデル[31])これは通常、前述の意味での「閉じた」モデルであるためである。特に、数学的な便宜のために、確率過程が既約で正の再帰性を持つと仮定していることが多いのである。これは、一意の定常分布が存在することを意味し[44]、それによって、オープンエンドの進化の可能性を排除している。すべての状態の確率がゼロではないオープンエンド進化のモデルを開発することは可能であるが、実際のオープンエンド進化でもそうでなければならないことは明らかではない。例えば、遺伝子型を構成するヌクレオチドの組み合わせは事実上無限にあるが、そのうちの少なくともいくつかは本当に致死的であると予想される。より実用的なレベルでは、ここで紹介した分析をもとに、小さなしきい値(ɛ>0)よりも大きな確率で発生する状態を実現可能な状態と定義すれば、同様の定理が証明できると考えられる。
計算可能性に関するすべての考慮事項が整数値関数に制限されていることを考えると、計算可能性の概念を より正確にする必要がある。集合値関数
より正確にする必要がある。集合値関数 は、2つの別々の計算可能関数で構成されていると考えることができる。各関数は整数値関数であるため、すでに説明した計算可能性の概念に適合する。最初の関数は、以前と同様に単純に計算可能な関数ϕ E(i)であり、その範囲は現在、実行可能な母集団状態のセットと見なされている。ここでの引数iは、もはや進化の時間ではなく、単にその意味を以下に説明するインデックスである。ϕで表す2番目の計算可能関数E *( n)であり、世代nの実行可能な母集団状態の数を次のように指定する。時間1でのすべての実行可能な母集団状態のセット、つまり
は、2つの別々の計算可能関数で構成されていると考えることができる。各関数は整数値関数であるため、すでに説明した計算可能性の概念に適合する。最初の関数は、以前と同様に単純に計算可能な関数ϕ E(i)であり、その範囲は現在、実行可能な母集団状態のセットと見なされている。ここでの引数iは、もはや進化の時間ではなく、単にその意味を以下に説明するインデックスである。ϕで表す2番目の計算可能関数E *( n)であり、世代nの実行可能な母集団状態の数を次のように指定する。時間1でのすべての実行可能な母集団状態のセット、つまり { ϕ E(1)、 ϕ E(2) 、…、{ φ E( K 1、ここ)} φ E *(1)= K 1。同様に、
{ ϕ E(1)、 ϕ E(2) 、…、{ φ E( K 1、ここ)} φ E *(1)= K 1。同様に、 ここで、 φ E *(2)= K 2、など。このようにして、同じ計算可能性の概念を集合値関数に適用できる。
ここで、 φ E *(2)= K 2、など。このようにして、同じ計算可能性の概念を集合値関数に適用できる。 それらをそのコンポーネントである整数値の関数ϕ E(i)およびϕ E *(n)に適用することによって。セット
それらをそのコンポーネントである整数値の関数ϕ E(i)およびϕ E *(n)に適用することによって。セット はすべてのnに対して有限であると仮定する。これにより、計算可能であることが保証される。それにもかかわらず、このセットが無限であるいくつかの定式化は依然として計算可能であり、したがって、以下の結果に依然として適合すると予想することは合理的であるように思われる。
はすべてのnに対して有限であると仮定する。これにより、計算可能であることが保証される。それにもかかわらず、このセットが無限であるいくつかの定式化は依然として計算可能であり、したがって、以下の結果に依然として適合すると予想することは合理的であるように思われる。
決定論的な場合と同様に、マッピングHに加えて、初期条件も指定する必要がある。次に、マッピングHに関して、 が時間nでの実行可能な母集団状態である場合、時間n +1での実行可能な母集団状態のセットは次の式で与えられる
が時間nでの実行可能な母集団状態である場合、時間n +1での実行可能な母集団状態のセットは次の式で与えられる 。ここで、サポートH(x)はH(x)積極的なサポートがある。の範囲
。ここで、サポートH(x)はH(x)積極的なサポートがある。の範囲 は、ある時点で実行可能なすべての状態のセットである(つまり、ϕ E(i))。同様に、状態は、それが実行可能である時間がある場合、進化的に達成可能である。完全な進化の理論は一つであるため、述語「X ∈ R Eは、」任意の人口の状態を考えると、我々はそれがいくつかの時間で実現可能であるかどうかを決めることができ、場合すなわち、決定可能である。
は、ある時点で実行可能なすべての状態のセットである(つまり、ϕ E(i))。同様に、状態は、それが実行可能である時間がある場合、進化的に達成可能である。完全な進化の理論は一つであるため、述語「X ∈ R Eは、」任意の人口の状態を考えると、我々はそれがいくつかの時間で実現可能であるかどうかを決めることができ、場合すなわち、決定可能である。
プログレッシブ進化の同じ定義は、決定論的ケースと確率論的ケースの両方で使用できる。これを正確に指定するには、次の見出語が必要である。
補題E.1。 決定論的ケースでは、進化が制限されていない場合(つまり、R E が無限大である場合)に限り、タイムステップごとに新しい状態が訪問されます。
補題E.2。 確率論的ケースでは、進化が制限されていない場合(つまり、R E が無限大である場合)に限り、タイムステップごとに少なくとも1つの新しい状態が実行可能である。
補題E.2のみの証明が与えられる(補題E.1は同様の方法で証明できる)。我々は、このセクションの残りの部分で、我々は表記法を使用し、その点に注意してほしいR E(nは)段階で(すなわち可能)訪問されている人口の状態の集合を示すためにn個のセット値関数の、 (すなわちないステップNをのϕ E(n))。同様に、ステップi = k 1 + k 2 +…+ k nによって訪問されるϕ E(i)の範囲を示する。
(すなわちないステップNをのϕ E(n))。同様に、ステップi = k 1 + k 2 +…+ k nによって訪問されるϕ E(i)の範囲を示する。
証拠。「各タイムステップで少なくとも1つの新しい状態が実行可能です」⇒「無制限の進化」。
タイムステップごとに少なくとも1つの新しい状態が実行可能である場合、 合計であるという事実はR Eが無限であることを意味するため、この含意の方向は明らかである。
合計であるという事実はR Eが無限であることを意味するため、この含意の方向は明らかである。
‘Evolutionunbounded’⇒’各タイムステップで少なくとも1つの新しい状態が実行可能です ‘。
アサーションとは反対に、代わりにR Eは無限大であるが、新しい状態が実行可能ではない時間n *があると仮定する。言い換えれば、ある時間n *の間、集合 は
は 。を満たする。次の時間ステップで実行可能状態の集合は、その後で与えられる
。を満たする。次の時間ステップで実行可能状態の集合は、その後で与えられる 、各要素のために、また
、各要素のために、また 、∃ N X < N *ように
、∃ N X < N *ように (仮説からの
(仮説からの )。したがって、各要素のために、
)。したがって、各要素のために、 我々はそれを持っている
我々はそれを持っている 場合、nはX < N *。したがって、
場合、nはX < N *。したがって、

E 1

E 2

E 3
したがって、誘導によって、R E ≡ R E(N * -1)、矛盾を生じる、有限である。▪▪
決定論的なケースでは、進化が制限されていない場合、計算可能関数ϕ E(i)は、iが増加するにつれて以前に達成された値を繰り返さないことに注意してほしい(上記の補題E.1)。ただし、確率論的ケースでは、進化に制限がない場合でも、ϕ E(i)は、iが増加するにつれて、以前に達成された値を繰り返すことができます。2つのケース間の重要な関係は、確率論的ケースでは、ϕ E *(n)は、ϕ E(i)は、対応する進化世代にグループ化され、そのような各グループ化には、常に少なくとも1つの新しい実行可能な状態が含まれる(上記の補題E.2)。
ここで、定理の証明に戻ると、決定論的な場合、補題E.1は、すべてのタイムステップで新しい人口状態が訪問されることを示している。そして、進化が進歩的である場合、時間の経過とともに訪問されるこれらの新しい状態のコード数が増加するように、人口状態を再コード化するいくつかの方法がある。同様に、補題E.2は、訪問された人口状態の一部が以前にも訪問された可能性があるものの、すべてのタイムステップで少なくとも1つの新しい人口状態が実現可能になることを示している。それでも、時間ステップごとに実行可能になる新しい状態のコード番号が時間とともに増加するように、母集団の状態を再コード化する方法があれば、進化は進歩的であると我々は言う。正式に は、世代nで新たに実現可能な状態のセットとして定義すると、
は、世代nで新たに実現可能な状態のセットとして定義すると、 これらの中で最小のものとして、すべてのnについて
これらの中で最小のものとして、すべてのnについて 、正の整数と母集団の状態の間に計算可能な全単射が存在する場合、進化は漸進的である。セットは有限であり、すべてのnに対して計算可能であるため、は合計計算可能関数である。
、正の整数と母集団の状態の間に計算可能な全単射が存在する場合、進化は漸進的である。セットは有限であり、すべてのnに対して計算可能であるため、は合計計算可能関数である。


次に、定理の証明は次のようになる。
定理E.6。「X ∈ R Eは、」(すなわち、決定可能であり、R Eは、場合再帰的である)、そして、計算一対一の正の整数によって人口状態のコードが存在する場合にのみ、 そのような進化の過程の対応する説明については、その、
そのような進化の過程の対応する説明については、その、 、
、 すべてのためのn。
すべてのためのn。
証拠。パート1:
 再帰的。
再帰的。
仮説により、すべてのnに対して次の ような計算可能な全単射が存在する。ここで、元のコーディングの任意の母集団状態xについて、全単射下の対応するコードとする。を定義する。明らかに、 ‘ ‘は有限で列挙可能であるように決定可能である。さらに、進化の進歩的な性質のために。したがって、 ‘ ‘も決定可能である。最後に、Sを使用して、進化的に達成可能な人口状態のセットを示する。我々はそれを持っている。定義上、、を取得することに注意してほしい。したがって、 ‘ X ∈ R Eは、 ‘も決定可能である。
ような計算可能な全単射が存在する。ここで、元のコーディングの任意の母集団状態xについて、全単射下の対応するコードとする。を定義する。明らかに、 ‘ ‘は有限で列挙可能であるように決定可能である。さらに、進化の進歩的な性質のために。したがって、 ‘ ‘も決定可能である。最後に、Sを使用して、進化的に達成可能な人口状態のセットを示する。我々はそれを持っている。定義上、、を取得することに注意してほしい。したがって、 ‘ X ∈ R Eは、 ‘も決定可能である。










パート2:R Eの再帰
 。
。
必要な計算可能な全単射を構築して、進化が次のように進行することを示すことができる。
以来R Eは再帰的で、我々は「ことを知っているのx ∈ R Eが」決定可能である。したがって、人口状態xを順番に取得し、次のアルゴリズムを使用してリストを下に移動する。
- もしX ∉ R E、それはK戻り、その時点まで、このような状態番目のkを奇数番目、
- もしX ∈ R E、およびそれがまだ新しいコード番号が割り当てられていない場合は、次の手順を実行する。
- —計算
 (つまり、xが初めて実行可能になったとき)、
(つまり、xが初めて実行可能になったとき)、 - -計算σ E(I)、で新たに実現可能な状態の全体のセットI、
- —表記を使用する| A | Aのカーディナリティを示すには、すべての|にコードを割り当てる。σ E(I)| 要素σ E(I)、始まることで| R E(i − 1)| + 1つの偶数、最大| R E(i)| 偶数、任意の順序、
- —リスト内の次の状態に移動する。
したがって、これ も偶数のセットであり、各タイムステップで実行可能な新しい状態は、時間の経過とともに常に大きなコード値を持つ。特に、
も偶数のセットであり、各タイムステップで実行可能な新しい状態は、時間の経過とともに常に大きなコード値を持つ。特に、 ポイント(i)および(ii)で上記のアルゴリズムを示すために使用する。ここで、C -1は、xを生成したコーディングの逆マッピングである(つまり、コードxを取り、対応する母集団の状態sを返する)。あり
ポイント(i)および(ii)で上記のアルゴリズムを示すために使用する。ここで、C -1は、xを生成したコーディングの逆マッピングである(つまり、コードxを取り、対応する母集団の状態sを返する)。あり
 ます。最後の等式は、事実から次
ます。最後の等式は、事実から次 の各要素が初めて決定σ Eは、(N + 1)(これは発生N |定義により、全てのそのような要素に対して+ 1)した後、コード2を代入する NSE( n)+ 1 | 最大2 | R E( n + 1)| これらの要素のために。もちろん、これらのコードの最小値は2 |である。R E( n)+ 1 | 与える
の各要素が初めて決定σ Eは、(N + 1)(これは発生N |定義により、全てのそのような要素に対して+ 1)した後、コード2を代入する NSE( n)+ 1 | 最大2 | R E( n + 1)| これらの要素のために。もちろん、これらのコードの最小値は2 |である。R E( n)+ 1 | 与える 。結果として、
。結果として、 | R E( n)| はnとともに厳密に増加している(補題E.2から)。▪▪
| R E( n)| はnとともに厳密に増加している(補題E.2から)。▪▪
決定論的なケースでは、進化が制限されていない場合、計算可能な関数φE(i)は、iが増加するにつれて、以前に達成された値を繰り返すことはないことに注意してほしい(上記のレムマE.1)。しかし、確率的なケースでは、進化が束縛されていない場合でも、φE(i)はiの増加に伴い以前に達成された値を繰り返すことができる。この2つのケースの重要な関連性は、ストキャスティックなケースでは、φE*(n)は、φE(i)の出力が対応する進化世代にグループ化されるとき、そのようなグループ化のそれぞれは、常に少なくとも1つの新しい実現可能な状態を含むようなものであるということである(上記のレンマE.2)。
さて、定理の証明に戻ると、決定論的ケースでは、lemma E.1は、新しい集団状態が時間ステップごとに訪れることを示している。そして、もし進化が進行性であるならば、時間の経過とともに訪れるこれらの新しい状態のコード番号が増加するように、集団の状態を再コード化する何らかの方法があるはずである。同様に、lemma E.2は、訪問された集団の状態が以前にも訪問されていたかもしれないが、各時間ステップで少なくとも1つの新しい集団の状態が実現可能になることを示している。それでも、各時間ステップで実現可能になる新しい状態のコード番号が時間とともに増加するように、集団の状態を再コード化する何らかの方法があれば、進化は進行性であると言える。形式的には、次のように定義する。
次に、定理の証明は次のようになる。
定理E.6。「X ∈ R Eは、」(すなわち、決定可能であり、R Eは、場合再帰的である)、そして、計算一対一の正の整数によって人口状態のコードが存在する場合にのみ、 そのような進化の過程の対応する説明については、その、
そのような進化の過程の対応する説明については、その、 、
、 すべてのためのn。
すべてのためのn。
証拠。パート1:
 再帰的。
再帰的。
仮説により、すべてのnに対して次の ような計算可能な全単射が存在する。ここで、元のコーディングの任意の母集団状態xについて、全単射下の対応するコードとする。を定義する。明らかに、 ‘ ‘は有限で列挙可能であるように決定可能である。さらに、進化の進歩的な性質のために。したがって、 ‘ ‘も決定可能である。最後に、Sを使用して、進化的に達成可能な人口状態のセットを示する。我々はそれを持っている。定義上、、を取得することに注意してほしい。したがって、 ‘ X ∈ R Eは、 ‘も決定可能である。
ような計算可能な全単射が存在する。ここで、元のコーディングの任意の母集団状態xについて、全単射下の対応するコードとする。を定義する。明らかに、 ‘ ‘は有限で列挙可能であるように決定可能である。さらに、進化の進歩的な性質のために。したがって、 ‘ ‘も決定可能である。最後に、Sを使用して、進化的に達成可能な人口状態のセットを示する。我々はそれを持っている。定義上、、を取得することに注意してほしい。したがって、 ‘ X ∈ R Eは、 ‘も決定可能である。










パート2:R Eの再帰
 。
。
必要な計算可能な全単射を構築して、進化が次のように進行することを示すことができる。
以来R Eは再帰的で、我々は「ことを知っているのx ∈ R Eが」決定可能である。したがって、人口状態xを順番に取得し、次のアルゴリズムを使用してリストを下に移動する。
- もしX ∉ R E、それはK戻り、その時点まで、このような状態番目のkを奇数番目、
- もしX ∈ R E、およびそれがまだ新しいコード番号が割り当てられていない場合は、次の手順を実行する。
- —計算
 (つまり、xが初めて実行可能になったとき)、
(つまり、xが初めて実行可能になったとき)、 - -計算σ E(I)、で新たに実現可能な状態の全体のセットI、
- —表記を使用する| A | Aのカーディナリティを示すには、すべての|にコードを割り当てる。σ E(I)| 要素σ E(I)、始まることで| R E(i − 1)| + 1つの偶数、最大| R E(i)| 偶数、任意の順序、
- —リスト内の次の状態に移動する。
したがって、これ も偶数のセットであり、各タイムステップで実行可能な新しい状態は、時間の経過とともに常に大きなコード値を持つ。特に、
も偶数のセットであり、各タイムステップで実行可能な新しい状態は、時間の経過とともに常に大きなコード値を持つ。特に、 ポイント(i)および(ii)で上記のアルゴリズムを示すために使用する。ここで、C -1は、xを生成したコーディングの逆マッピングである(つまり、コードxを取り、対応する母集団の状態sを返する)。あり
ポイント(i)および(ii)で上記のアルゴリズムを示すために使用する。ここで、C -1は、xを生成したコーディングの逆マッピングである(つまり、コードxを取り、対応する母集団の状態sを返する)。あり
 ます。最後の等式は、事実から次
ます。最後の等式は、事実から次 の各要素が初めて決定σ Eは、(N + 1)(これは発生N |定義により、全てのそのような要素に対して+ 1)した後、コード2を代入する NSE( n)+ 1 | 最大2 | R E( n + 1)| これらの要素のために。もちろん、これらのコードの最小値は2 |である。R E( n)+ 1 | 与える
の各要素が初めて決定σ Eは、(N + 1)(これは発生N |定義により、全てのそのような要素に対して+ 1)した後、コード2を代入する NSE( n)+ 1 | 最大2 | R E( n + 1)| これらの要素のために。もちろん、これらのコードの最小値は2 |である。R E( n)+ 1 | 与える 。結果として、
。結果として、 | R E( n)| はnとともに厳密に増加している(補題E.2から)。▪▪
| R E( n)| はnとともに厳密に増加している(補題E.2から)。▪▪
付録F. 効果的に無限のシステム
本文中で考えた進化の単純化された系は、潜在的な集団状態の空間が無限であることを仮定し、非束縛進化(すなわち|RE|=∞)に焦点を当てている。しかし、実際の進化のシステムは、遺伝物質の構成要素に限界があるという理由だけで、必然的に有限であると主張する人がいるかもしれない。この反論に対しては、2つの可能性がある。まず、哲学的なレベルでは、ある特定の進化のシステムは有限であるかもしれないが、それにもかかわらず、進化論は抽象的なものであり、進化のダイナミズムのある特定のインスタンスとは無関係であることを望むかもしれない。これは、数論の文脈において、数を数える必要のある有限のものだけを扱う必要があるにもかかわらず、有限の制限を前提としない抽象的な数論を望むという事実に非常によく似ている。そして、このような否定完全な数の理論が不可能であるように [32-35,41]、進化が進歩的でない限り、進化生物学にも不可能なのである。
第二に、より実用的なレベルでは、DNA/RNAが提供する遺伝のデジタルな性質が、可能な集団状態の数が膨大であるという点で、このようなシステムを実質的に無限にすることは明らかである。このセクションの残りの部分では、事実上無限という概念を正確に説明する。簡単にするために、以下では決定論的なシステムに焦点を当てる。
ここで、|RE|=∞の場合、関数は、任意の入力に対して有限のステップ数で評価できる場合、計算可能(かつ全体)であることを思い出してほしい[37](付録B)。したがって、述語「x∈RE」は、その特性関数が、任意の入力値xに対して、有限のステップ数で評価できるならば、decidableである。同様に、マッピング
rsif20110479-i94.jpg 定理の計算可能性は、任意の入力に対して、有限回のステップでコード番号を返すことができる場合である。
しかし、|RE|<∞のとき、「x∈RE」という述語は、常に有限のステップでREの完全なカタログ化を行うことができるので、常に決定可能である。単に、nの値を増やしていくためにφE(n)を連続的に評価すればよいのである。appendix Eのlemma E.1によると、REは有限なので、最終的には以前に訪れたことのある値を得ることになり、その時点からシステムは以前に訪れたことのある状態を単に再訪することになる。
これらの観察は形式的には正しいのであるが、有限系におけるデジタル継承の重要な結果を捉えていない。特に、不定形遺伝の文脈における有限系の計算可能性の自然な類似性は、出力が有限のステップ数で得られるという要件ではない。むしろ、有限回のステップで出力が得られ、そのステップ数が状態空間の大きさに依存しない有限回の境界|RE|を超えないことが必要である。例えば、この有限状態空間の定義では、「x∈RE」という述語は、その特性関数が有限回のステップで評価でき、かつ、そのステップ数が|RE|に依存しないある有限境界を超えない場合、決定可能となる。このように、|RE|の大きさに関わらず、一定数以上の計算ステップを必要としないことが保証されている。
これらのアイデアを公式化するためには、異なるサイズの状態空間|RE|を考慮することが何を意味するのかを正確に示す必要がある。これは次のように行う。まず、本文で使われている無限状態空間の状況を考える。ここで、φE(n)は進化過程に対応する計算可能な関数を表する。
次に、有限状態空間のプロセスを計算可能な関数FEη(n)で定義する。ここで、n = η + 1は、以前に訪れた集団の状態が再訪問される最初の時間であり、FEη(n) = ϕE(n) for all n ≤ ηとする。なお、η=|RE|であることから、ηは状態空間の大きさである。このようにして、任意の有限状態空間プロセスは、有限プロセスが以前に訪れた状態を再訪し始めるη + 1の時点まで、基準となる無限状態空間プロセスであるφE(n)と時間的に同一となる。したがって、異なるサイズの状態空間、ηを考えることができ、η→∞の限界ケースが本文の無限状態空間に対応する。有限の場合の定義を以下のように修正する。
定義F.1。述語「X ∈ R Eは、任意の入力のために、場合」*決定可能であり、X、存在T特性関数は、そのような<∞ を超えないで評価することができるTは手順、Tは無関係であるη(すなわち、システムの独立したサイズ)。
を超えないで評価することができるTは手順、Tは無関係であるη(すなわち、システムの独立したサイズ)。
定義F.2。正の整数による母集団状態の1対1のマッピングは、 任意の入力に対して、マッピングがTステップ以下で評価できるようなT <∞が存在する場合、*計算可能である。ここで、Tは独立している。η。
任意の入力に対して、マッピングがTステップ以下で評価できるようなT <∞が存在する場合、*計算可能である。ここで、Tは独立している。η。
テキストの主定理は、次の場合に成り立つことがわかる。R E | 上記の定義を使用する場合は<∞。特に、
定理F.3。「X ∈ R Eは」である*あれば決定可能、及び、*計算一対一の正の整数のサブセットによって人口状態のコードが存在する場合にのみ、 そのような進化の過程の対応する記述こと、
そのような進化の過程の対応する記述こと、 、満足
、満足  すべてのため のn ≤ η。
すべてのため のn ≤ η。
テキストの主定理とは1つ異なることに注意してほしい。つまり、進歩的な進化の特性の変化。ここで、R Eは有限であるため、プロセスが繰り返される前に時間の経過とともに増加する量がある場合、進化は進行性であると言う。また、定理のステートメントの「計算可能」および「決定可能」の変更された定義に加えて、計算可能性の他のすべてのインスタンスもこの変更された定義を使用することに注意してほしい。
この修正された定理は、本文と類似しているため、正式な証明のスケッチのみが示されている。リコールそのF E η(Nは)関心のある有限の進化システムに対応する計算関数である。
証明(スケッチ)。パート1:∃ 
 。⇒ ‘ X ∈ R E ‘ *決定可能。
。⇒ ‘ X ∈ R E ‘ *決定可能。
前と同じように、任意の入力xを取り、その新しいコードを見つける 。仮説によれば、必要なステップ数は、システムサイズに依存しない定数によって制限される。次に、我々は、連続的に評価するために始めることができるF E η(nは値増加のため)のnを。我々は、ステップ数は任意のため、この計算で必要と仮定し、N ≤ ηとは独立しているη。出力はのものと同一であるので、これは妥当な仮定であるφ E(N)ときN ≤ η、およびステップの数を評価するのに必要なφE( n)は、任意のnのηに依存しない。各出力に我々 、上記マッピングを適用することができ得ることは、仮説により、で増加する、 N ≤ ηを。仮説によれば、必要なステップ数は、そのような各アプリケーションのηとは無関係である。
。仮説によれば、必要なステップ数は、システムサイズに依存しない定数によって制限される。次に、我々は、連続的に評価するために始めることができるF E η(nは値増加のため)のnを。我々は、ステップ数は任意のため、この計算で必要と仮定し、N ≤ ηとは独立しているη。出力はのものと同一であるので、これは妥当な仮定であるφ E(N)ときN ≤ η、およびステップの数を評価するのに必要なφE( n)は、任意のnのηに依存しない。各出力に我々 、上記マッピングを適用することができ得ることは、仮説により、で増加する、 N ≤ ηを。仮説によれば、必要なステップ数は、そのような各アプリケーションのηとは無関係である。


我々はどちらか、進行我々は、(i)に達するように、N = η前到達するNそのため 、我々は式(II)の値に達する、またはNとなる
、我々は式(II)の値に達する、またはNとなる 前に、N = ηを。いずれの場合も、この時点までに到達してい
前に、N = ηを。いずれの場合も、この時点までに到達してい なければ、
なければ、 到達することはないため、 ‘ ‘は決定可能である。したがって、 ‘ X ∈ R Eは、 ‘も決定可能である。さらに、(i)が関係する場合、決定する前に必要なステップ数は
到達することはないため、 ‘ ‘は決定可能である。したがって、 ‘ X ∈ R Eは、 ‘も決定可能である。さらに、(i)が関係する場合、決定する前に必要なステップ数は ;以下である。(ii)が関係する場合、このステップ数は正確にに等しくなり
;以下である。(ii)が関係する場合、このステップ数は正確にに等しくなり ます。また、
ます。また、 は有限でηに依存しないため、 ‘ x∈ R Eは”だけでなく、*決定可能である。
は有限でηに依存しないため、 ‘ x∈ R Eは”だけでなく、*決定可能である。
パート2: ‘ X ∈ R E ‘ *決定可能⇒∃*

次のように、人口状態と適切なコーディングの間に必要な*計算可能な全単射を構築できる。まず、人口状態の効果的なコーディングを行う。仮説では、ステップ数が「決定するために必要なのx ∈ R Eを任意のは」xが有限とは独立しているη。したがって、次のアルゴリズムを適用することにより、人口状態xを昇順で進めることができる。
- -もしX ∉ R E、Kそれまでのような状態番目、使用kは、その新たなコードとして奇数番目。
- -もしX ∈ R E、計算μ I(F E η(I)= X)、および使用私の新しいコードとして番目の偶数。
状態xを進めると、(i)または(ii)のどちらに関係するかに関係なく、それぞれに必要なステップ数はηに依存しない。したがって、任意の状態のコーディング手順全体はηにも依存しない。つまり、コーディングは必要に応じて*計算可能である。▪▪
