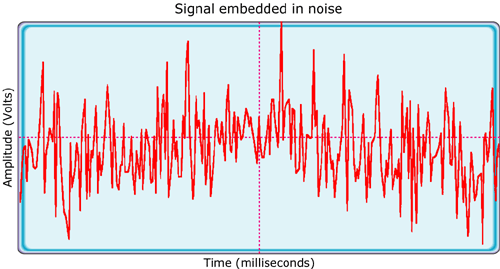
The Signal Importance of Noise
2015, Vol.44(2) 306-328
マイケル・メイシー1、ミレーナ・ツヴェトコヴァ1
要旨
ノイズは、線形モデルにおける説明できない分散や、予測可能なパターンのランダムな乱れなど、残差のカテゴリーとして広く認識されている。したがって、形式的なモデルでは、世界はノイズがなく、社会的ダイナミクスは決定論的であるという単純化された仮定がしばしば課される。
ノイズが因果的に重要であるとされる場合、それはしばしば非効率性、予測不可能性、あるいは不均質性の源であると仮定される。私たちは、複雑なシステムのダイナミクスを理解するためのノイズの理論的重要性を実証するために注目すべき最近の社会学的研究をレビューする。
広く受け入れられている仮定に反して、これらの研究は、ノイズが効率と予測可能性を高め、多様性を低下させる条件を明らかにしている。最後に、決定論的な仮定は無邪気な単純化ではない、という方法論的な警告を発している。
キーワード
エージェントベースモデル、分析社会学、複雑系、コンピュータシミュレーション、決定論、確率モデル、ゲーム理論、ランダムエラー
はじめに
ああ、多くの矢が、無作為に送られて、射手が意図しない印をつけるのを発見する。ウォルター・スコット卿(1771-1832)
科学は、根底にある因果関係のあるプロセスの働きを示す、非ランダムなパターンを探す。これらのパターンはしばしばノイズに覆われ、それを取り除くことで根底にあるシグナルを明らかにする必要がある。統計学では、調査の動機となるのは基礎となる母集団の中心的傾向であり、くじ運によってもたらされるランダムな変動ではない。
線形モデルでは、誤差項は説明できない分散であり、誤差がランダムである限り、分析者は通常これを無視する。測定モデルでは、私たちが探している信号を不明瞭にしない限り、ある程度のノイズを予想し許容する。シグナルは調査の対象であり、ノイズではない。
私たちは別の視点を持っている。ノイズの「シグナル重要性」とは、結果を理解するためにノイズが決定的に重要である場合があるということである。ノイズを取り除けば、説明を取り除くことができるかもしれない。これは、私たちがモデル化している世界がノイズに満ちているからではない。
観測された結果の分布における中心傾向からのランダムな偏差を取り除くことは、その変動が本質的にランダムなプロセスに対応するものであれ、単にまだ理解されていない系統的なプロセスに対応するものであれ、何の問題もない。
むしろ、この問題の裏側に注意を喚起したい。その偏差が本質的にランダムなプロセスに対応するものであれ、単にまだ理解されていない系統的なプロセスに対応するものであれ、ある結果を生み出すと想定される行動からランダムに逸脱すると仮定することには問題があるのだ。
簡単に言えば、私たちの議論は、世界がノイジーだろうかどうかということではない(私たちはノイジーであると信じているが)。ノイズを排除した決定論的理論モデルから得られる結果の理論的信頼性について議論しているのだ。
ノイズは「予測できない」という意味ではなく、「不確実である」という意味である。不確実性は、事象が稀に起こること、意図せず起こること、予測できないことを意味する必要はない。不確実性は、確率が0か1でない限り、大小を問わず、あらゆる可能性を持つ事象を特徴づけることができる。
ノイズの多い事象は、意図的なもの(レストランを選ぶためにコインを投げるときなど)、意図的でないもの(間違いや誤認など)がある。
ノイジーな事象は、起こりうる結果に対する確率分布が分かっている場合は予測可能であり、分布が分からない場合は予測不可能である。珍しいか典型的か、意図的か偶発的か、予期されるか意外か、ノイジーな出来事は確実に予測することはできない。
赤と青の有限個の玉で満たされたカゴがあり、すべての玉に一意の番号が振られ、一個の玉以外はすべて青であるとする。そして、ランダムに1個のボールを引く。赤玉と青玉の数がわかれば、青玉を引く確率がわかり、青玉の割合が増えるにつれて、その確率は漸近的に1に近づいていく。
しかし、いくら確率が1に近づいても、青が選ばれることがほぼ確実な場合であっても、何色が選ばれるかは確実には分からない。それは、ある色の玉が選ばれる確率は同じでなくても、かごの中の玉はすべて同じ確率で選ばれるからだ。どの玉も等しい確率で選ばれるので、抽選の順番はランダムになる。つまり、自己相関がゼロで、独立かつ同一に分布する事象が発生することになる。
赤と青の数が分からないので、青を選ぶ確率が分からないという場合もあるが、この条件は、ケージの中のすべての玉が等しい確率で選択されるかどうかとは無関係である。確率が分かっていても分かっていなくても、その過程は決定論的ではなく確率論的であり、すべての抽選の結果は本質的に不確実である。

確率論的モデルと決定論的モデルの区別は、ノイズの有無である。ノイズは不偏であるため、調査対象である中心的な傾向や潜在的なパターンを捉えるために、ノイズを除去することが望まれる。常微分方程式に基づく解析モデルは、しばしば対象プロセスが決定論的であるという単純化された仮定に依存しており、この仮定はモデルをより数学的に扱いやすくしている。
計算機モデルもまた決定論的であることが多いため、デバッグが容易であり、変化のない状態として平衡状態を厳密に特定できるようなダイナミクスを可能にする。というのは、決定論的なモデルが経験的にあまり妥当でないからではなく、ノイズがシステムのダイナミクスに重要な影響を与えることがあり、安全に無視することができないからだ。
この考えは歴史的に物理学に根ざしており、気体の運動論、熱力学、統計力学(例:Prigogine 1976)の基礎となっているが、社会科学、特に社会学ではあまり顕著ではない。しかし、分析社会学(動的で複雑な社会システムにおける因果過程の研究)への関心が高まるにつれ、行動規則や局所構造への非常に小さな摂動が複雑なシステムのダイナミクスに極めて非ランダムな結果をもたらす可能性への認識が高まってきた。
特に、ノイズはしばしば非効率、予測不可能、多様性と関連付けられるが、ある条件下では、ランダムな摂動はより効率的で予測可能、かつ多様性の低い結果を導くことがある。私たちは、ノイズがこのような非常に直感に反する効果を持つという研究をレビューする。
このような応用では、決定論的モデルは経験的に妥当でないだけでなく、決定論を緩和したときには導かれない一連の仮定の論理的含意を指摘することで、理論的に誤解を招く可能性がある。私たちは、社会的相互作用におけるノイズをモデル化するための分析的・計算的アプローチについて、ゲーム理論から始めて、方法論的概観を簡単に説明する。ゲーム理論家は長い間、ノイズの説明的重要性を認識してきた。
ゲーム理論家は、計算間違い、誤認識(どのボタンが押されたかを誤認する「震える目」)、誤操作(間違ったボタンを押す「震える手」)により生じる最良応答戦略からのランダムな逸脱をモデル化する。ベストレスポンスとは、他のプレイヤーが選択した戦略から、あるプレイヤーにとって最適な結果をもたらす戦略のことである。
すべてのプレイヤーが最適な応答を選択したとき、ナッシュ均衡が成立するという。プレイヤーはいくつかの理由で最良回答から外れることがある。第一に、完全に合理的なプレイヤーは、それにもかかわらず、二人が戸口ですれ違おうとするときのように、他者の意図について誤って推測することがある(van de Rijt and Macy 2009)。

第二に、他者の行動の監視が不完全であったり、情報の処理に誤りがあったりするために、他者の戦略を誤認・誤導する可能性がある(Axelrod and Dion 1988)。最後に、行為者が最適な反応を正しく計算しても、実施に誤りが生じることがあり、Selten (1975) はランダムな手の「震え」として特徴づけている。
ノイズは様々な行動を表すことができるため、様々な方法でモデル化することができる(Helbing 2010).最も一般的には、ランダムな偏差は母集団において独立であり、基礎となる行動に関して不偏であると仮定される。
これは、すべての行為者に同一のエラー確率を割り当て、他のすべての可能な行動から一様にランダムに最適でない行動を引き出すことによって実現される。その代わりに、偏差が偏る傾向がある場合、非最適な行動は異なる分布を使用して描画することができる(例えば、Pineda, Toral, and Herna´ndez-Garc´a (2009)における一様分布ノイズの効果とMa¨s, Flache, and Helbing 2010における正規分布「白」ノイズの効果を比較する)。
さらに、最適な応答戦略からの逸脱は、異なる条件下では可能性が高くなることも低くなることもある。例えば、多くの利害が絡んでいる場合,行為者はより注意深く熟考し、コストのかかるミスを犯す可能性は低くなると仮定される。
これは、最適な対応から外れる確率をペイオフの関数としてモデル化することで実現されてきた(例えば、Binmore and Samuelson 1994; McFadden 1973; Montanari and Saberi 2010; Seymour 2000; Young 2011)。
このようなゲーム理論の発展により、他の応用分野でもノイズの重要性が認識されるようになった。特に、計算モデルによって、研究者は複雑なシステムのモデルにおけるノイズの効果を系統的に調査することができるようになった。
計算機的手法により、数学的に扱いやすくするための単純化された仮定を緩和することができる。特に、エージェントベース計算(ABC)モデルは、ノイズのない世界という単純化された仮定を緩和することを可能にしている。
方程式に基づく解析的アプローチとは対照的に、ABCモデルは母集団の単一のモデルを、それぞれが自律的だが相互依存的な行為者(または「エージェント」)に対応するモデルの母集団に置き換えるものである。ゲーム理論のように、モデラーは異質なエージェントの特性に関するミクロレベルの仮定を提供し、ネットワーク構造などの文脈的な仮定に対応する制約の下で相互作用させる。
母集団の特性は、エージェント間の相互作用から現れる。この方法によって、研究者はミクロレベルの行動仮定が母集団レベルで持つ論理的含意を特定することができる。ゲーム理論と同様に、これらの含意はしばしば非常に直感に反しており、モデルによって示唆された仮説を検証するための実証的研究の動機となる(Clark 1991; He and Wong 2004; Macy 1995; Ruoff and Schneider 2006; Strang and Still 2004; Valente 1996; Willer, Kuwabara, and Macy 2009)。
ABCモデルは純粋に決定論的なモデルもあるが、ほとんどのモデルは確率論的である。確率モデルの結果は、単一の不可避的な結果ではなく、一般に確率分布である。このレビューでは、確率モデルにおいて、結果の分布の中心的傾向が、他の同一の決定論的モデルにおける固有の結果と一致しないことが判明した場合について概観する。例えば、ノイズが新技術の多様性を高めるという逆説的な効果がある。
- 新しい技術や組織的実践の多様性とその平均的成功の両方を増加させる。
- 文化的多様性を崩壊させ、文化的拡散を多様化させる
- 少数民族に寛容でない集団において、居住区の統合をより促進させる。
- 集団行動は起こりやすいが、拡散はしにくい。
- ウイルス性の情報や病気の蔓延を加速させる一方で、コストやリスクの高いイノベーションの普及を遅らせたり妨害したりする。
私たちは、計算機モデルの社会科学的応用において確認されたノイズの3つの驚くべき意味を中心に、これらの研究をグループ分けした。ノイズは効率を高め、予測可能性を向上させ、多様性を低下させることができる。
ノイズと効率性
ノイズはしばしば効率や最適性を阻害すると考えられているが、最近の研究では、ノイズが逆の効果をもたらすこともあることが示されている。まず、ノイズが社会的に非効率的であるモデルを検証し、次にノイズが個人的あるいは集団的に有益であるいくつかの逆説的な状況を考察する。
少量のランダムネスでもシステムを最適な均衡から遠ざける可能性があり、特にその均衡が脆弱な場合はなおさらである。その究極の例が、即座に大規模な報復を行う戦略に基づく核超大国間の均衡である(相互確証破壊[MAD]として知られている)。世界は今のところその危険を免れているが、この均衡は、人類文明にとって致命的な結果をもたらす事故の可能性を完全に排除できないことに脆弱である。

もっと身近な例では、偶発的な損傷が引き金となって、反目しあう隣人たちの間で逆恨みのサイクルが延々と続くということがある。Kollock(1993)は、「目には目を」というガンディーの言葉を引用し、「囚人のジレンマ」を繰り返し行うことによって、少量のノイズがいかに協力関係の崩壊につながるかを示した。
このゲームでは、プレイヤーは「協力」と「亡命」という2つの行動を選択する。協力は最大の相互利益をもたらすが、ゲームの1回のプレイでは、各アクターは必ず亡命した方が個々に有利になる。しかし、ゲームが継続的に行われる場合はそうではない。
ロバート・アクセルロッドは有名な研究で、将来の相互作用における相互協力から得られる累積的利益が、アクセルロッドが「未来の影」と呼ぶ現在の瞬間における離反の誘惑に勝る可能性を示した(アクセルロッド 1984; Axelrod and Hamilton 1981)。

アクセルロッドはゲーム理論の第一人者を招き、戦略を提出させ、コンピュータを使ったトーナメントで互いに競わせた。この戦略は、協力することから始めて、その後、相手の前の行動と同じように反応する単純な戦略である。
この戦略は、いい人(挑発されない限り離反しない)であり、また寛容(相手が離反しなくなったら協力を再開する)だが、素朴(挑発されたら必ず報復する)でないために成功したのである。
TIT FOR TAT(しっぺ返し)
しかし、Kollock (1993)は、潜在的に破壊的な弱点を示した。TIT FOR TAT(しっぺ返し)は、報復の無限サイクルを引き起こすランダムなエラーに弱いのである(Molander 1985; Reeves and Pitts 1996)。
彼はコンピュータ・シミュレーションを用いて、より寛大で寛容な戦略(例えば、TIT FOR TWO TATS)(倍返し)が少量のノイズの存在下でより良いパフォーマンスを示すことができることを明らかにした。
Signorino (1996)は関連する脆弱性を明らかにした。TIT FOR TATは十分に寛容でないだけでなく、悔恨の念もない、つまり、自分自身のいわれのない離反の後に罰を受け入れることができない。相手の「震える手」や自分の誤認によって引き起こされる逆恨みの無限ループを防ぐには「許し」が必要だが、自分のミスや相手の誤認を正すには「悔恨」が必要なのである。
Helbing and Yu (2009)は、囚人のジレンマにおいて、ノイズが協力を阻害するもう一つの方法を示している。最も成功した隣人の戦略を真似るというノイズのない世界では、協力者が空間ネットワーク上に集まっていれば協力は維持される。しかし、ランダムな突然変異によって協力者が離反すると、協力は崩壊する。このとき、離反者の報酬が高いため、離反は急速に広まる。
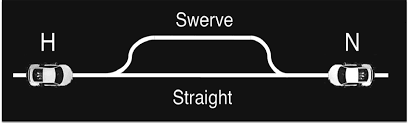
チキンレース
また、ノイズは混合戦略均衡としてゲームに取り込まれることもある。例えば、チキンゲームでは、2人のドライバーが互いに速度を上げて向かい合い、それぞれが対向車を避けるためにハンドルを切るか、そのままコースを維持するかの2つの選択肢を持つ。

このとき、一方のプレーヤーが衝突を避けるためにハンドルを切り、もう一方のプレーヤーがコースを維持することが集合的最適均衡の結果となる。この均衡は、両プレイヤーにとって同時に同等かそれ以上の代替結果が存在しないという意味で、集合的に最適である。
ゲーム理論家は、各プレイヤーが2つの可能な選択肢のうち1つだけにコミットしていることから、これを純粋戦略均衡と呼んでいる。また、混合戦略均衡も存在する。この均衡では、各プレーヤーは、ハンドルを切ることと留まることに正の確率を割り当て、両プレーヤーは2つの行動の間で無関心である。
しかし、両者ともランダムに進路変更を選択し、両者とも避けたい衝突を起こす危険性が出てきた。したがって、一方のドライバーが他方のドライバーに道を譲り、何も起こらない純粋戦略均衡の上で行動を調整する方が、両プレイヤーにとって有利になる。
これらの研究は、社会的相互作用の決定論的モデルにおいて、ノイズを除去することを仮定することの危険性を示している。ノイズがなければ、互恵/報復の戦略、協力者のクラスタリング、大惨事につながるかもしれない行動を避けようとする一方的な意思によって、協力関係を維持することができる。しかし、決定論的な仮定は驚くほど脆弱な単純化であることが判明した。ゼロでない誤差は、協力が盛んな条件下で社会秩序を崩壊させるのに十分である。
ノイズ
コロックやヘルビングとユーが示したランダム・エラーに対する脆弱性は、ヘビや山火事や風邪のように、ノイズは一般に避けたいものだという私たちの素朴な直観と共鳴する。しかし、これらの一見迷惑なもの(それ自体は必ずしもノイズではない)のように、ノイズもまた必要不可欠なものであることが、次に紹介する研究で明らかにされている。
ペナルティキック
通常、ランダムな誤差は合理的な行為者の最適な選択を妨げるが、ゲーム理論家は意図的なランダム化が個人的に最適な戦略である状況を特定した-自分の意図を他のプレイヤーに推測させ続ける必要がある場合である。その好例がサッカーのペナルティキックである(Chiappori, Levitt, and Groseclose 2002)。

もし、キッカーがある方向を好み、ゴールキーパーがそれを知っていれば、ゴールキーパーが有利になり、逆に、キッカーがゴールキーパーに偏りがあることを知っていれば、ゴールキーパーが不利になる。したがって、「mixing it up」のように混合戦略をとることで、双方ともランダムに方向を選択する方が有利になるのである。
相手を推測させることで、混合戦略はPKや「ペニー合わせ」、「ジャンケン」などのゼロサムゲームに特有の最適な対応となる。ゼロサムゲームでは、あるプレイヤーの損失は別のプレイヤーの利益となる。また、相互利益と相互損失の機会があるゲームでは、混合戦略が最適な対応となりうる。
囚人のジレンマ
ランダムな誤差が個人の結果だけでなく集団の結果をも改善するような状況もある。簡単な(そしてやや些細な)例は、Kollock (1993)が指摘した問題の裏返しである。
もし人々が繰り返し起こる囚人のジレンマで、他人が協力することを信用しないためにのみ離反すると、ランダムな離反が無限の報復のサイクルを引き起こすのと同じように、ランダムな協力の行為が無限の報復のサイクルを引き起こすことがある(Bendor、Kramer、およびSwistak 1996)。
Helbing and Yu (2009)は模倣と移動を伴う空間的な囚人のジレンマゲームにおいて、ノイズの同様の効果を発見している。プレイヤーは、成功した隣人を模倣し、自分の戦略がより成功するような空いている場所に移住する。
このような仮定の下で、著者らは、ノイズが集合的に最適でない均衡から最適な均衡への移行を引き起こすことを見出した。誰もがほぼ常に離反する世界では、ランダムな突然変異によって、離反者に搾取されやすいにもかかわらず、協力が成り立つだけの協力者を持つ小さなクラスタが最終的に作られるのだ。
成功駆動型移動”は離反者を引き寄せるが、協力者が高密度になることで侵略から身を守ることも可能である。このように、協力は偶然の出来事によって自然に生まれ、それがカスケードを引き起こすのである。著者らはこう結論付けている。
「協力の度合いはノイズの強さに応じて低下するが、適度なノイズは協力の優勢への移行を加速することさえある」(p.7)。
より一般的には、ノイズは最適でない均衡を早期に破壊し、エージェントに優れた解決策を発見させることができる。この可能性は、金属を加熱することで原子の動きにノイズを発生させ、その結果、結晶構造の不完全性が減少するという冶金学の「焼きなまし」のプロセスの背後にある。
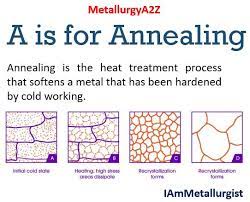
このような過程を経て、コンピュータ科学者や数学者は、確率的最適化に基づく探索アルゴリズムを開発した。探索が最適でない解の近くで行き詰まった場合、ランダムな摂動がアルゴリズムを自発的に探索空間の未知の領域へと押しやる(Spall 2003)。
生物進化は、自然界における確率的最適化の説得力のある例であり、ランダムな誤差(遺伝子突然変異という形で)が適応的な解の探索に寄与している。ランダムな突然変異は、生物の適応度を上げたり下げたりするので、本質的に適応的な機能はない。
進化が適応的な問題に対してより良い解決策を見出すことを可能にするのは、突然変異ではなく、自然選択である。しかし、突然変異がなければ、自然淘汰は最終的に集団の遺伝的多様性を枯渇させることになる。異質性がなければ、組換えは部分的な解を基に、より適応的な戦略を見出すことができない。
突然変異は、異質性を減少させる傾向のある選択圧に直面して、異質性を回復させる。もちろん突然変異が多すぎるのも最適とはいえないが、集団が「偽のピーク」に陥る可能性のある不均一なフィットネスランドスケープを進化的に探索するためには、少量が不可欠である。
進化的探索の原理は、技術革新や組織学習にも応用されており、例えば、Marchによる搾取と探索のトレードオフのモデル(March 1991; Helbing, Treiber, and Saam 2005; Lazer and Friedland 2007; Miller, Zhao, and Calantone 2006も参照)などが知られている。March は、「exploitation of old certainties」 は短期的な利益をもたらすが、「exploration of new possibilities」 は長期的に組織のパフォーマンスを向上させると主張している。
搾取にはベストプラクティスのコピーが含まれるが、これは生物進化における自然淘汰のプロセスに類似しており、最適でない解決策を早期にロックインしてしまうという同じ問題を持つ。探索は、ランダムな探索と体系的な独立した探索を可能にすることで、選択と搾取のために競合する可能なソリューションの多様性を高める。
ノイズと予測可能性
線形モデルでは、勾配パラメータは1つ以上の共変量の状態に基づく結果の予測を可能にし、誤差項は予測値からの観測値のランダムな偏差を表す。同様に、ランダムな測定誤差は、調査対象の正確な同定を妨げます。より一般的には、ある事象がランダムであれば、確率分布が分かっていても、その事象の特定の発生を予測することはできない1)。
したがって、直感的には、あるプロセスの結果が、そのプロセスにおけるノイズのレベルが高くなるほど予測困難になることを示唆している。しかし、本節では、少量のノイズの導入が結果の予測可能性を低下させるのではなく、むしろ向上させるという社会力学の研究をレビューする。
Granovetter(1978)の集団行動に関する閾値モデルは説得力のある例証を提供してくれる。Granovetterは、ある個人が集団行動に参加する意志を持つようになる臨界参加者数を閾値としてモデル化した。
動員の成功に対する個人の関心が弱ければ弱いほど、他の人がどれだけ参加する気があるかを待つ傾向が強くなる。個人の閾値の分布によっては、参加者が増えるごとに他の参加者が参加するきっかけとなるカスケードが発生する可能性がある。
Granovetterは、カスケードが閾値の分布のギャップに達すると失速することを示した。極端な例として、全員がN 1の閾値を持っているとする。つまり、全員が参加しない限り、誰も参加しない。当然のことながら、この集団における集団行動は失敗する可能性が非常に高い。
同様に、全員がゼロのしきい値を持っていれば、集団行動は成功することが保証されている。しかし、全員の閾値が1であったとしよう。成功する動員への関心の度合いは閾値ゼロの場合とほぼ同じだが、閾値1の結果は閾値N 1の場合と同じである-誰もが他の誰かが最初の動き手とならないかと周りを見回しており、したがって誰も参加しない。これらの定型化された図解は、Granovetterの論文の重要な洞察を示している。参加者の均衡水準は、動員を成功させるための関心の水準と一致する必要はないのである。
これらの例の結果は、決定論的ナッシュ均衡である。ナッシュ均衡であるのは、参加水準が、各個人が他の人の行動を考慮して最善の対応を選択したようなものだからだ。決定論的なのは、結果がモデルのパラメータに割り当てられた値によって完全に制御され、したがって何度実験を繰り返しても同じになるからだ。したがって、参加者の均衡レベルは決して変わらない。
ここで、このモデルが決定論的ではなく、確率論的であるとする。具体的には、閾値1の集団の全員が、他の何人がすでに参加したとしても、あるεの確率で参加するとする。ここでも、誰もが誰かが先に参加するのを待ち続けている。
しかし今度は、誰かが閾値ではなく偶然に行動し、カスケードが発生する。このことは、Granovetterの洞察が、理論的には興味深いが、決定論的な仮定に基づいており、経験的にはありえないことを示している。
確率的な閾値モデルからは、直感に反するような洞察が得られる。εが非常に小さい場合、各個人がランダムなイベントを経験する確率は非常に小さいが、誰かがカスケードを引き起こす確率はNとともに指数関数的に増加する(厳密には、トリガーイベントの確率は1 (1 e)N) である)。
この洞察は、集団行動に関する理論的文献の中で最も重要な発見の一つである「集団規模のパラドックス」(Oliver and Marwell 1988)を示している。集団が大きければ大きいほど、最初に行動しようとする偶然の異常者(あるいは異常者の小集団)が存在する確率が高くなる。
グラノベッターの決定論的モデルにノイズを導入すると、さらなる驚きがある。システムの挙動はより予測しやすくなる。もし全員の閾値がわかっていれば、決定論的モデルは動員の結果を完全に予測することができる。問題は、閾値が未知である場合に発生する。
グラノベッターの目的は予測可能性をモデル化することではないが、重要な結果は、閾値の分布におけるギャップの位置によって、動員に対する関心の平均レベルにかかわらず、ゼロからN人の参加者までのすべての可能な結果が潜在的な均衡となることである。
観察者が成功した動員に対する平均的な関心を合理的に推定し、そこから平均的な閾値が0に近いかN 1に近いかを推定することは難しいことではない。対照的に、カスケードを停滞させる原因となる閾値分布のギャップを事前に見つけることははるかに困難である。
決定論的モデルでは、そのようなギャップに対して非常に敏感であるため、結果を予測することは困難である。しかし、プロセスが確率的であると仮定すれば、この決定論的な均衡は、ランダムで特異な参加決定によって乱され、カスケードが進行する可能性がある。
その結果、確率過程の長期的な傾向は、結果に対する関心の高さに対応することが期待できる。つまり、母集団内の結果に対する関心の度合いを事前に知っていれば、ノイズを加えることで結果をより予測しやすくすることができる。
逆に言えば、世界はノイズに満ちているという仮定によって、集団行動が成功する可能性は、成功への関心の高さに応じて高くなるという確信を持つことができる。もし、グラノベッターの決定論的世界に住んでいたら、その自信はグラノベッターが指摘するような理由で不当なものとなっていただろう。

グラノベッターは決定論的な仮定を緩めず、ノイズが結果をより予測しやすくする可能性にも留意しなかった。これに対して、ゲーム理論家は、進化生物学者であるSmithとPrice(1973)の先駆的な研究を皮切りに、このノイズの逆説的効果を重要な理論研究へと発展させた。
SmithとPriceはゲーム理論を用いて、自然が平均的なペイオフに基づいて戦略を選択する進化的プロセスをモデル化した。この進化論的応用は、古典的ゲーム理論の重要な限界に直面することになる。この仮定は、ビジネス、政治、軍事の専門家が、一連の手の最後の一手から推論して最善の初手を特定する後方帰納法の使い方を学んだ上で行うゲームでは正当化されるかもしれない。
しかし、この仮定は、合理的な先見性ではなく、試行錯誤に依存する最適化プロセスには、目的論的な誤りをもたらす。Smith and Price (1973) は生物学的な見地に基づき、一度すべてのプレイヤーが採用した戦略でも、ランダムに変異した代替戦略に侵入される可能性のあるナッシュ均衡を排除する改良として、「進化的安定性」を提唱している。
例えば、囚人のジレンマを繰り返し行う場合、TIT FOR TATはナッシュ均衡だが、常に協力するランダムな変異株によって侵され、その結果、常に欠損する別の変異株によって集団が侵されやすくなるので、進化的に安定とは言えない。
進化の安定性の発見とほぼ同時に、セルテン(1975)は、ランダムな摂動の影響に耐えられない均衡を排除する別の改良-「震える手」-を提案した。例えば、2人の友人が家で1人で食事をするよりもレストランで会って食事をする方が楽しいが、レストランで1人で食事をするのは本当に嫌だとする。

このゲームには、自宅でもレストランでも、友人たちが一緒に食事をするナッシュ均衡が2つある。しかし、レストランでの食事は手が震えるほど完璧ではない(携帯電話のない世界を想定している)。それは、何らかの予期せぬ偶然の出来事によって、その友人が現れない可能性が常に少しはあるからだ。
Foster and Young (1990)はナッシュ均衡に関連して、確率的安定性(stochastic stability)と呼ばれる洗練された均衡を提案した。彼らはまず、システムが継続的に摂動にさらされると仮定する。
そして、確率的に安定な均衡とは、摂動の割合がゼロに近づくにつれて、長期的に優勢になる均衡である。外食の例では、自宅で食事をすることがリスク優位の戦略である。FosterとYoungは、時間が無限大になり、誤差の確率が徐々に消失すると、ほとんどすべての時間においてリスク優位の戦略が選択されることを示した。
これらの問題をゲーム理論で抽象的に表現したため、経験的な社会科学者には解が人工的に見えるかもしれないが、3つの均衡の精密化(進化的安定、震える手、確率的安定)には、均衡がランダムな摂動の影響に耐えなければならないという直感的に魅力的な共通の基本原理が表れている。
グラノベッターの閾値モデルが明確に示しているように、ノイズに頑健でない均衡は、あまり予測力を持たない。このような脆弱な均衡を可能な解の集合から取り除くことで、モデルの予測力は、しばしば劇的に向上させることができる。
ノイズ、多様性、拡散ノイズがいかに効率を上げるか(下げるか)、予測可能性を上げるか(下げるか)見てきた。次に、ノイズが多様性を増加させる(または減少させる)研究に目を向ける。これらのモデルでは、人々はダイナミックな社会的ネットワークにおいて、自分の属性を隣人に合わせて変えるか、隣人を自分の属性に合わせて変えるか、あるいはその両方によって、隣人とより類似した存在になる。ここでは、まず文化同化の研究から始め、次に民族分離の研究、そして拡散のモデルで締めくくる。
文化的同化先に述べたノイズと最適化の議論から、自然淘汰による進化の基本原理、すなわち、遺伝的多様性を減少させようとする淘汰圧に直面したときに、遺伝的多様性を回復するためのランダムな突然変異の必要性に注目することになった。
ランダムな変異がもたらす多様化効果は非常に直感的だが、ノイズが逆の効果をもたらすこともあることがわかった。このことは、Klemm ら(2003a 2003b;参照:De Sanctis and Galla 2009)が、Axelrod(1997)の文化的同化に関する先行研究を拡張した論文で最近実証している。
アクセルロッドのモデルは、文化的多様性が持続的であると同時に不安定であるというパラドックスに対処するものである。Greig (2002)は、文化的マイノリティが同化の力に対して頑健であることを強調しているが、国連教育科学文化機関(UNESCO)が2001年の白書で表明した多様性の将来についてのより悲観的な見通しを受け入れる人も少なくない。
たとえば、世界には約6,800の言語が存在するが、その約半数は絶滅すると予想されている(Crystal 2000)。Axelrodは、同化と多様性のダイナミクスを、広く観察されている2つの社会的メカニズムを組み合わせたエージェントベースのモデルを使って調査した。
同類性(類似した他者と交流する傾向)と社会的影響(交流する相手とより類似するようになる傾向)である。これらのプロセスは、集団が文化的同質性へと向かうと予想される自己強化のダイナミズムを示唆している。しかし、アクセルロッドは、Flache and Macy(2011)が「a cultural analog of biological speciation」(生物学的種分化の文化的類似性)と呼ぶもののために、必ずしもそうではないことを示した。
これは、共通の祖先を持つ有性生殖生物は、ある閾値を超えると交配ができなくなることと類似している。その結果、同類愛と社会的影響力が、同化から保護された安定した文化的領域を「特定」することができる。つまり、局所的な収束を生み出すのと同じプロセスが、グローバルなレベルでの多様性を維持するのだ。
アクセルロッドの説明は優美で説得力があるが、文化的形質がランダムな突然変異の影響を受けないという決定論的な仮定に決定的に依存していることが判明している。Klemmとその共同研究者たち(2003a, 2003b;参照:De Sanctis and Galla 2009)は、文化的形質のランダムな摂動という、経験的にもより妥当な可能性を導入している。
彼らのモデルは、直感が示唆するように、ランダムな突然変異が局所的な多様性を増加させることを確認した。しかし、局所的な不均質性の増大は、グローバルなレベルでの文化的多様性の崩壊を引き起こす可能性がある。
その理由は、2つのグループからなる完全に両極化した集団が、他の内集団のメンバーとはあらゆる点で同一であり、外集団のメンバーとは正反対である、という単純なケースを考えてみればわかる。
このような状況では、本来なら相互同化をもたらすはずの集団間の文化的接触や影響力が排除される。つまり、両極化した集団は均衡を保っているのだ。しかし、予測可能性の議論でも述べたように、決定論的な均衡はランダムな摂動に対して極めてもろいものになりうる。
少量の文化的ノイズが共通基盤を作り出し、そうでなければ浸透しない文化的境界を越えて相互作用を可能にすることがある。この相互作用によって、残された差異が減少し、さらに多くの相互作用が生まれる。こうして、以前は異質だった隣人が次第に似てきて、差異がなくなり、より大きな地域の周囲に新しい文化的境界が形成される。
やがてこの境界も摂動によって破られ、それまで似ていなかった隣人の間に共通の形質が生まれ、これが繰り返され、差異がなくなるまで続く」(Flache and Macy 2011:972-973)。…..。
突然変異率が十分に高ければ、結果として生じる文化の乱れが安定した文化圏の形成を妨げ、Centolaら(2007:918)は、地域の慣習への適合性がないことを示すために、このパターンを「文化的アノミー」(cultural anomie)と特徴づけている。
フラッヘとメイシーが指摘するように、文化的アノミーは多様性と混同してはならない。後者は、内部的に均質な地域内で文化的収束が必要であり、互いに十分に異なるため、時間が経過してもその独自性を維持することができる。アノミーとは、互いに異なる個体が、互いに惹かれ合う以上に衰退していくために、異なる地域が合体できないことを意味する」(Flache and Macy 2011:973)。
つまり、ノイズは多様性を2つの側面から攻撃しているとFlache and Macyは述べている。ノイズの割合が十分に低ければ、摂動は文化的地域間の境界を突破し、同化を促進する。ノイズの割合が十分に高ければ、擾乱は局所的な収束を妨げる。したがって、文化的多様性は摂動率の狭い範囲でのみ実現可能であり、その範囲は人口規模の増加に伴って漸近的に狭まっていく(Flache and Macy 2011)。
民族隔離文化的分化に対するノイズの影響は、居住ネットワークの民族隔離という文脈でも研究されている。Schelling(1971)はJournal of Mathematical Sociologyに掲載された論文で、民族の多様性に寛容な集団においてもティッピングプロセスが完全な分離につながることを示した。しかし、グラノベッターやアクセルロッドのように、シェリングは意思決定が決定論的な閾値関数に基づくと仮定していた。
同系列の隣人の割合が臨界閾値以下である限り、誰も移動することはなく、閾値以上では決して留まることはないのである。BruchとMare(2006)は、広く知られた論文の中で、Schellingの結果は頑健ではないと主張した。
人口レベルでの転倒プロセスは、個人レベルでの転倒プロセスを仮定したSchellingの成果であり、隣人の民族構成が50%というような単一の閾値を除いて、個人は近隣の民族構成の変化には反応しないのである。
BruchとMareのモデルは、Schellingが想定したよりも、人々は近隣の民族構成の小さな変化に対してはるかに敏感であるという、より経験的に妥当な仮定を捉えている。著者らがSchellingの閾値関数を連続関数に置き換えたところ、分離はほとんど消滅した。より正確には、ある閾値までは民族の多様性を許容する集団と比較して、集団外の隣人が増えるたびに通知する集団では、分離レベルが低くなったのである。
この非常に直感に反する発見を受けて、van de Rijt, Siegel, and Macy(2009)はBruchとMareのモデルを注意深く再現した。しかし、彼らはBruchとMareが報告したこととは逆のことを発見し、BruchとMare(2009)は結局、元の発見がコーディングエラーによるものであったことを認めたのである。
Bruch and Mareと同じモデルを用いているが、「バグ」がないため、Van de Rijtらは、民族構成のわずかな変化に敏感に反応することで、一般に分離は少なくなるのではなく、多くなることを発見している。
BruchとMareが報告した低いレベルの分離は、移動するかどうかの決定が非常にランダムであるという追加的な仮定によって引き起こされている。Schellingのモデルでは、引っ越しの決定は近隣の民族構成によって完全に決定される。
一方、BruchとMareは、決定が偶然に大きく左右されると仮定した。民族構成への感応度ではなく、このようなノイズの高さが、分離独立を低下させるのだ。人種差別主義者の集団であっても、ランダムな混合のレベルが十分に高ければ、統合される傾向がある。
van de Rijtらは、純粋に決定論的なものから純粋にランダムなものまで、あらゆるレベルのノイズを調査することによって、民族構成に対する感受性によってノイズの効果が増幅されることを発見した。人々が集団外の隣人に気づくたびに、ランダムな移動が「エラーカスケード」の引き金となり、その論理はSchellingが明らかにしたティッピング・プロセスと同じである。
外集団の隣人が多すぎる地域から引っ越すという一つの決断が「ホワイトフライト」のカスケードを引き起こすように、外集団の隣人が多すぎる地域にランダムに引っ越すと、民族統合につながるエラー・カスケードが引き起こされる可能性がある。
民族構成のわずかな変化に敏感に反応することで、変化する近隣地域から離れるという非ランダムな決定によってカスケードが引き起こされた場合は分離へ、引っ越してくるというランダムな決定によってカスケードが引き起こされた場合は統合へと、両方向のカスケードが促進される可能性がある。
このように、ノイズレベルが高くなると、エラーカスケードによって不寛容な集団のメンバーが統合される可能性が出てくる。彼らは、外集団の隣人が増えるたびに現在地への不満が高まっていく。逆説的だが、van de Rijtらは、民族構成の小さな変化にはほとんど無関心な寛容な集団では、こうしたカスケードが起こりにくくなる可能性を示している。
イノベーションの拡散 BruchとMareやvan de Rijtらによってモデル化された住宅格子上のランダムな移動は、隣人間の結びつきがランダムに形成・切断される動的ネットワークとしてもモデル化することが可能である。ランダムな結びつきは、離れたクラスター間の接触を容易にし、文化的同化や民族的分離のダイナミクスだけでなく、病気、情報、流行、社会運動の広がりにも影響を与える。
このようなネットワークの橋渡しの重要性は、社会学で最も引用されている論文の一つであるGranovetter(1973)の「弱い絆の強さ」についての研究によって示されている。グラノベッターによれば、親しい友人間の絆と比較して、知人間の絆は信頼が低く、交流の頻度も少なく、コミットメントも弱い傾向があるという。
しかし、このような弱い絆の強さは、親しい友人のクラスタをつなぐ強い絆とは対照的に、ネットワークのクラスタ間の橋渡しをする傾向があることである。これらの橋は社会的ネットワークの遠隔地に情報へのアクセスを提供し、拡散を促進し、社会的統合を促し、地球上で無作為に選ばれた2人の人間の間に有名な「6度の隔たり」が観察されることを説明している。
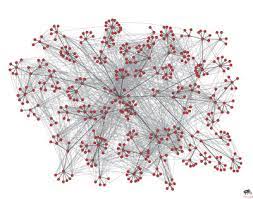
しかし、この「小さな世界」は、社会的ネットワークが高度にクラスター化し、ほとんどの人が緊密に結びついた「小さな友達の輪」の中に組み込まれているという証拠とどのように整合させることができるだろうか。
その答えはWatts and Strogatz (1998; Watts 1999)によって発見された。彼らはまず高度にクラスタ化されたネットワークから始め、ランダムに選ばれた結びつきをランダムに選ばれたノードとの結びつきに置き換えることで構造的なノイズを導入した。
そして、ある伝染病(例えば、生物学的あるいは文化的ウイルス)があるノードからネットワーク全体に広がるのに必要な時間を測定した。予想通り、ランダムな配線がない場合、伝染病は、すべての結びつきがランダムなネットワークよりもはるかにゆっくりと広がっていくことがわかった。
しかし、「スモールワールド」ネットワークではどうだろうか。スモールワールドでは、10個に1個のタイしかランダムに変化していないため、クラスター化が進んでいる。ワッツとストロガッツは、伝染病が完全にランダムなネットワークとほぼ同じ速度で広がっていくことを発見した。
言い換えれば、高度にクラスタ化されたネットワークの構造に少量のランダム性があると、伝染性の病原体、求人情報、ウイルスの噂、キャッチーなフレーズなど、ある個人から別の個人に容易に移る伝染病の伝播が著しく加速されるのだ。
この「スモールワールド」効果は、社会的世界をつなぐ「接着剤」を形成しているのは、親しい友人間の緊密なパターン化された関係ではなく、関係性のランダム性であることを示唆していると考えることができる。しかし、Centola and Macy(2007)による追跡調査では、ネットワークのノイズはWatts and Strogatzが発見したのとは逆の効果も持ちうることが明らかになった。
彼らのスモールワールド実験では、WattsとStrogatzは伝染病の閾値が1であること、つまり、伝染病は感染した1人の隣人との接触によって広がることができると仮定している。しかし、CentolaとMacyは、多くの社会的伝染病が1より大きい閾値を持つことを指摘している。
例えば、2人以上の友人から同じニュースを聞くことは冗長だが、2人以上の友人から同じアドバイスを聞くことは強化される。コストのかかるイノベーションを採用したり、リスクの高い社会運動に参加したり、宗教色の濃いコミュニティで避妊具を使用するなど、議論を呼ぶような慣習に参加する場合も同様である。これらの社会的伝染では、その行動をすでに採用している人の数が多ければ多いほど、ネットワークの隣人に伝わる自信と正当性の感覚は大きくなる。
Centola and Macy (2007)は、まずWatts and Strogatzの実験を再現し、高度にクラスタ化したネットワークの構造をランダムに摂動し、伝播の速度を観察した。次に、感染した隣人が1人(彼らはこれを「単純な伝染」と呼んでいる)から2人以上(「複雑な伝染」)に採用の閾値を上げることを除いて伝染実験を繰り返した。
ランダムな再配線は拡散を促進しないだけでなく、複雑な伝染の拡散を完全に阻止した。情報や病気のような単純な伝染病はランダムな結びつきが有効だが、複雑な伝染病の伝播には局所的なクラスターに見られる冗長構造が必要であり、ランダムな再配線はそれを損なってしまうのである。ネットワーク上のノイズが少なければ単純な伝染病が最大限の伝播速度を得ることができるように、ランダムな再配線が少なければ複雑な伝染病の離陸を妨げることができる。
結論
社会科学者は一般的にノイズを、線形モデルにおける説明のつかない分散や、系統的なパターンのランダムな乱れといった、残差のカテゴリーとみなしている。したがって、ノイズは社会生活の根底にある因果的なメカニズムを見えなくする無意味で無関係な振る舞いに過ぎず、したがって、調査対象をより正確に特定し測定するために除去しても問題ないように思われることもある。
しかしながら、ここ数十年の間に、社会的相互作用におけるランダムエラーの説明的重要性に対する認識が高まってきている。これらの研究を概観すると、行動規則や局所構造に対する小さな摂動が、いかに社会システムのダイナミクスや均衡を劇的に変化させうるかがわかる。
相互依存的な行動の複雑なシステムにおいては、間違いは増幅される可能性がある。たった一つの誤りが、行動変化のカスケードや新しい解空間への移行を引き起こし、その結果、ダイナミクスを全く新しい予想外の方向へ導くことがある。
広く知られている仮定とは逆に、私たちがレビューした研究は、ある条件下では、ランダムな摂動が非常に逆説的な効果をもたらし、結果をより効率的に、より予測可能に、そしてより多様にすることができることを実証している。ノイズは、全体として最適でない局所的な均衡を乱し、集団として好ましい結果をもたらすことがある。
脆弱な均衡を排除することで、解集合のサイズを小さくし、結果をより予測しやすくする。
ノイズは局所的な不均質性を高めるが、その結果、社会的相互作用が促進され、グローバルな多様性を低下させる可能性がある。ランダムな移動は「エラー・カスケード」を引き起こすことによって近隣の民族分離を減らすことができるが、このカスケードは民族の多様性に寛容な集団よりも民族に敏感な集団の方が起こりやすいと言われている。
少数のランダムな結びつきは、情報や病気の伝播のために私たちの世界を縮めることができるが、こうした弱い結びつきは、議論を呼ぶ信念やリスクの高い集団行動といった社会的伝染病の早期蔓延にはつながらない。
これらの研究から得られるメッセージは、ノイズを取り除いた決定論的モデルには注意を払うべきだということである。もし決定論的モデルの予測がノイズに対してロバストでなければ、特に多次元非線形システムにおいて、重要なダイナミクスを隠してしまうかもしれない。
ノイズは、自然言語で表現されたモデルでは認識することが難しい、非常に直感に反する効果を持つことがある。ゲーム理論やABCモデルは、しばしば直感に反する効果を明らかにし、識別し、分析する努力に非常に有用であることが証明されている。しかし、個人の行動が完全に決定され、完璧に実行され、完全に知ることができ、完全に予測可能であるという形式的なモデルは、経験的にありえないだけでなく、非常に誤解を招く可能性がある。
謝辞
Michael Ma¨s, Andreas Flache, Dirk Helbing, and the members of the Social Dynamics Laboratory at Cornellの貢献に謝意を表したい。
利益相反の宣言
著者は、この論文の研究、著者資格、出版に関して潜在的な利益相反がないことを宣言した。
資金援助
著者は、本論文の研究、執筆、出版に関して、以下の資金援助を受けていることを明らかにした。本論文は、著者らが米国国立科学財団の助成金(SES 1260348)の支援を受けている間に作成された。
注
1. すべてのランダムな事象は確率が分かっていても予測不可能だが、予測不可能な事象は必ずしもランダムではない。例えば、暗号鍵を知らない観測者は、暗号化された非ランダムな数値列の次の値を予測することができない。
* *
