Contents
The Genesis of Constructal Theory

マックス・ボーダーズ
2024年3月20日
自然界に普遍的に存在する樹木のような維管束構造を紹介する芸術的コンポジション。中心には、複雑に枝を広げた雄大な木があり、木のような構造の真髄を象徴している。この木の周囲には、上から見た川の枝ぶり、葉の繊細な葉脈、人間の血管の複雑なネットワーク、空に浮かぶ稲妻の枝ぶりなど、さまざまな類似したパターンの表現が微妙に統合されている。これらの要素が風景に調和的に溶け込み、自然界におけるこれらのパターンの相互関連性と偏在性を際立たせている。このイメージは、畏敬の念と自然のデザインの複雑な美しさを呼び起こすものでなければならない。
人生は自然で自発的な変化の連続である。それに抵抗してはいけない-それは悲しみを生むだけだ。現実は現実である。物事がどのような形であれ、自然に前へと流れていくに任せよ。
-老子
1989年、ルーマニア国民が独裁者ニコライ・チャウシェスクを政権から強制的に追放したのと同じ年、エイドリアン・ベジャンはノースカロライナ州にあるデューク大学の著名教授に就任した。彼のキャリアを決定づけた理論になるものを、彼はまだ明確にはしていなかったが、ある意味ではすでに骨身にしみて知っていた。
ベジャンはルーマニアで過ごした幼少期を覚えている。共産主義の下では、物事はあまりうまく流れなかった。ブラックマーケットが暗黒の小川のように形成され、国家当局は人々が求めるものを供給できなかった。情報も制限されていたので、人々は本や雑誌、レコードを密輸した。インターネットはまだSFの世界だった。
冷戦のさなか、ルーマニアの店頭から肉が消え始めた頃、獣医だったベジャンの父は鶏を孵化させ始めた。彼は卵の内部を照らすライトボックスを持っており、胚が適切に成長していることを確認することができた。

エイドリアン・ベジャン 出典:mems.duke.edu
「ティーンエイジャーの私は、毎日目の前で展開される成長を、畏敬の念と驚きをもって見つめていました。血管系が成長し、殻の内面にしっかりと広がっていくのです」とベジャンは言う。
私が見ているデザインは、学校で描いていた色つきの地図に描かれていた川の流域と同じであることにも気づいた。ニワトリの胚が球体の内側で進化しているように、ドナウ川流域は球体の地球の外側で進化していたのだ。
これらの記憶は、プルースト的なコンストラクタル法のベースとなり、一度理解すれば至るところで目にすることができるほど強力なアイデアとなった。
コンストラクタル法というと高尚に聞こえるが、その考え方はこうだ: 自然システムから人間システムまで、あらゆる種類のシステムにおいて、物事の流れが良くなるとシステムは存続する。そして物事の流れが良くなると、自然界には良い流れの産物であるパターンがあることに気づき始める。
「コンストラクタル法が科学にもたらした活気は[…]伝染し、理論自体も非常に常識的で簡潔かつ有用であるため、まったく疑う余地のない分野の仲間たちともっと広く議論されるべきだ」とベジャンは言う。
若きベジャンは1969年、奨学金を手にMITに入学した。彼は数学の天才だったが、英語は合格点程度だった。彼はまた、アメリカ史上最も退廃的な時代にアメリカに到着した。祖国とのコントラストは深かった。彼は東欧圏の緊縮財政を離れ、目もくらむような製品やサービスの数々を発見した。この豊かさは彼にも影響を与えたに違いない。
1969年の来米から1996年にコンストラクタル法を発表するまでの間に、ベジャン教授は英語を上達させ、機械工学の博士号を取得し、デューク大学の教授職に就いた。フランスのナンシーで、著名な物理化学者イリヤ・プリゴジンの講演を聴講することになるまでには、さらに数多くの出版物とさらに10年を要した。
不愉快なことに、ベジャンはノーベル賞受賞者と意見が合わないことに気がついた。知る人ぞ知る、イリヤ・プリゴジンは水の上を歩く。彼は複雑系理論の名付け親であり、今日の多くの偉大な思想家や科学者の肩の上に立つ巨人である。
この有名な人物は、科学界の常識に共鳴し、川の流域や三角州、私たちの肺の空気の通り道、稲妻など、自然界にあふれる樹木状の構造はアレアトワール(サイコロを投げた結果)であると主張した。つまり、同じようなデザインの根底には何もない。宇宙的な偶然の一致なのだ。
彼がそう言ったとき、何かがひらめいた。ピンときた。私は、プリゴジンと他の誰もが間違っていることを知っていた。彼らは盲目ではなかった。これらの樹木のような構造の類似性は肉眼でも明らかだ。彼らに見えなかったのは、これらの多様な現象の設計を支配する科学的原理だったのだ。私は一瞬にして、世界は無作為の事故や偶然や運命によって形成されたのではなく、目もくらむような多様性の背後には、予測可能なパターンのシームレスな流れがあるのだと悟った。
その瞬間、コンストラクタル法が生まれたのである。
ダラムに戻る飛行機の中で、エイドリアン・ベジャンはこう書いた:
有限サイズの(流れの)システムが時間的に持続する(生きる)ためには、その構成は、その流れにますますアクセスしやすくなるように進化しなければならない。
この原則は、エイドリアン・ベジャンの研究の核心であり、経済全体における資本と資源の動きについて多くのことを説明している。しかし、この点についてはまた別の記事で触れよう。
Claude 3:加速主義とコンストラクタル法について
加速主義とコンストラクタル法の関連性については、いくつか興味深い示唆があります。
加速主義は、資本主義や技術進歩のプロセスを加速することで、究極的にはそれらを乗り越えたポスト資本主義の世界に至ると考える思想です。加速主義者は、技術の発展と社会の変化を阻害するのではなく、むしろ積極的に促進することを主張します。
この点で、加速主義はコンストラクタル法の「流れを良くする」という考え方と一致しているように見えます。技術や社会の「流れ」を加速することで、より良いシステムへと進化させようとする発想は、コンストラクタル法の原理に通じるものがあるでしょう。
また、加速主義は既存のシステムの限界を乗り越えようとする点で、コンストラクタル法の「有限サイズのシステムが持続するためには、流れにアクセスしやすいように進化しなければならない」という考えとも共鳴します。加速主義者は、資本主義というシステムの限界を、その内部からの加速によって突破しようとしているのです。
ただし、加速主義には社会的・政治的なイデオロギーとしての側面があるのに対し、コンストラクタル法はあくまで自然界のシステムに関する科学的理論です。両者を安易に結びつけることには注意が必要でしょう。
また、加速主義に対しては、社会的な不平等を悪化させかねないといった批判もあります。コンストラクタル法の観点からも、「流れを良くする」ことが常に望ましい結果をもたらすとは限らない点には留意が必要です。
いずれにせよ、加速主義とコンストラクタル法の関係性についてはさらなる学際的な探究の余地がありそうです。社会システムの進化について、両者の知見を結びつけることで新たな洞察が得られるかもしれません。
フラクタル、ルール、複雑性
私、ハカン・ヤシャルカンは、自作のPythonコードを使ってフラクタル図形を作ることを楽しんでいる。フラクタルは、それぞれの構造の魅惑的で美しい細部に没頭しながら、私がくつろぎ、休息し、瞑想できる聖域を作り出してくれる。フラクタルパターンの静謐な複雑さを探求し、静寂と内省の時を求める人々に安らぎの隠れ家を提供するために、私と一緒に参加しよう。

フラクタルワールドのHakan Yasarcanによるフラクタル。
大学時代のルームメイトは、古いパソコンでマンデルブロ・フラクタル図形を書いていた。1994年のある日、彼はLSDを飲んで何時間もフラクタルを見ていた。私は人生でいろいろなことをやったが、LSDはやったことがなかった。それでも私は彼と一緒に見ていた。フラクタルのイメージに感動するのに、アシッドは必要なかった。その蔓、葉、螺旋に触発され、私は旅に出た。もちろんフラクタルは単なる方程式であり、フラクタル画像はその方程式の表現にすぎない。そこに魔法はない。しかし、幾何学を視覚化すると、神の暗号にアクセスしたような気分になる。
フラクタルという言葉を聞いたことがない人は、身の回りを見回してみてほしい。葉脈の繰り返しの分かれ目から、古代のオウムガイの螺旋状の部屋まで、私たちは当たり前のようにフラクタルを見ている。再帰はどこにでもある。単純な幾何学図形が際限なく繰り返され、複雑な構成を生み出している。このような図形は自然のいたるところで見つけることができる。コンピュータを使えば、山のような風景や人工的な植物、本物を模倣した幻覚のような川の水系を作り出すことができる。これらの画像はほとんど無限に拡大することができる。フラクタルな川の三角州をたどっていくと、別の三角州が現れる。小川にズームインすれば、流域を持つまったく新しい環境を発見できる。
それ以来、私はいたるところでフラクタル図形を目にするようになった。ルームメイトになる前は、ブノワ・マンデルブロが誰かも知らなかった。しかし、これらの美しい形は、私の心を新しい可能性の領域へと開いてくれた。フラクタルへの新たな興味を武器に、私はカオスシステムと複雑性理論を探求し始めた。
そのルーツは虚数を含む複雑な数式にあるが、ルールは簡単に理解できる。
まず、創発と複雑性という2つの概念だ。創発とは、システム内の低次の要素間の比較的単純な相互作用の豊富さから新しいパターンが生じることである。複雑性とは、高次のパターンが要素の総和よりもどの程度大きいか(そしてその高次のレベルで研究できるか)ということである。複雑系の例としては、蜂の巣、動物の神経系、生物、経済、銀河系などがある。
私はこれらの分野との接触から、5つの基本的な教訓を得た:
- システムのルール どのような創発システムに関しても、ルールは重要である。ルールがなければシステムは成り立たないし、ましてや創発はありえない。ルールを変えれば、システムも一緒に変わる。
- 単純なルール。複雑なシステムを作るには、比較的単純なルールが必要だ。ルールが複雑になればなるほど、創発は起こりにくくなる。システム内の要素や「エージェント」は通常、複雑なルールに従うには間抜けすぎる(あるいはコストがかかりすぎる)ため、シンプルなルールの方が良いのである。
- ボトムアップ。創発システムには、設計者も中央当局も必要ない。これらの複雑な秩序は、ハチであれ粘菌であれ人間であれ、システム要素が特定のルールセットに従って行動することだけを要求する。システムは、各要素のルール指向の行動から創発される。
- 秩序あるカオス。自己組織化システムは頑強である。理論生物学者のスチュアート・カウフマンは、「生命は多くの面で秩序とカオスの間に位置する体制に向かって進化している。厳密な秩序とカオスの間のスイートスポットにあるシステムを見つけるとき、私たちは深遠な多様性を見出す。そして私たちは良いルールを見つけるのだ。
- バタフライ効果。初期条件の小さな変化が、システムの別の場所で予測不可能な大きな変化を意味することがある。これはバタフライ効果として知られるようになった。「秩序あるカオスを発見した気象学者エドワード・ローレンツは、「非周期的な振る舞いをする物理系は予測不可能であることに気づいた」と述べている。
この基本的な教訓を胸に、私は出撃した。
エラン・ヴィタル?
しかし、私の心に疑問が残った。なぜ “多くの面で “類似しているのか?自己組織化とルールに関係する理由があることは分かっていたが、その中途半端な答えには何かが欠けていた。ダーウィン以後、そのような力、ましてやそれを動かす生気などというものを、ほとんどの人は嘲笑してきた。
しかし、なぜオウムガイの殻はフィボナッチ数列や黄金比を表現するのだろうか?木の葉のフラクタルとどう関係があるのだろうか?社会経済現象は、ある条件下でどのようにフラクタル的パターンを示すのだろうか?なぜ単純なルールから複雑な社会秩序が生まれるのか?
エラン・ヴィタルのアイデアそのものをつまみ食いしているにもかかわらず、進化論的ヒューマニストのジュリアン・ハクスリーも同じような疑念を抱いていた:
ニューヨークに最後に行ったとき、五番街とビジネス街を後にして、バワリー近くの雑踏に散歩に出かけた。そしてそこにいる間、私は突然、安堵と自信を感じた。そこには[哲学者アンリ]ベルクソンのエラン・ヴィタール(生命力)があり、同化によって生命が、ここでは人間の姿に具現化されてはいるが、進化の最も早い時期にそうであったように、大きな圧力を及ぼしていた。
ハクスリーはそれに近づいていた。
「進歩の原動力」としての「圧力」という考えは、文学的な気まぐれや単なる比喩の域を出ない。
それはコンストラクタルな思考である。
血管社会
喧騒と富、そこに流れがある。
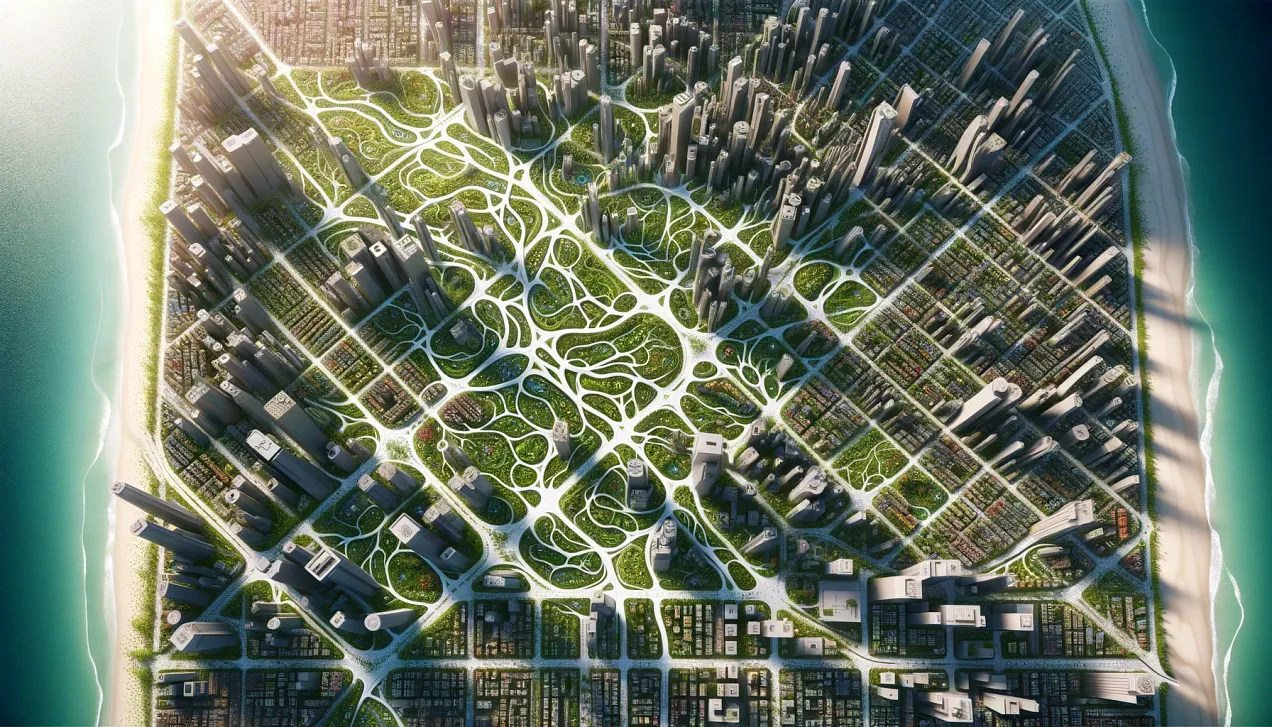
ベジャンの「コンストラクタル法」に従ってデザインされた、上空から見た街並み。血管や木の根の枝分かれを模して街路や建物が配置され、複雑で自然な血管システムのようなレイアウトになっている。この都市は、有機的な要素と都会的な要素が調和したもので、毛細血管のように都市構造を縫うように緑地が配置され、重要な臓器を思わせる大きな公園をつないでいる。建築様式はさまざまだが、シームレスに統合され、都市全体の人、資源、エネルギーの効率的な流れを促進する。全体的な外観は、都市そのものが持続可能性と回復力のために最適化された、呼吸する生命体であることを示唆しているはずだ。
マックス・ボーダー
2024年3月21日
昨日は、エイドリアン・ベジャンのコンストラクタル法の起源について述べた。今日は、「フローの法則」というレンズを通して、人間社会のマクロなプロセスを調査するために、ちょっとクリックしてみよう。
動くものはすべてフロー・システムである。エイドリアン・ベジャンによれば、生物であれ無生物であれ、すべてのフロー・システムは、より広い環境で遭遇する流れに基づいてその構造を生成するのだという。つまり、進化は生物学の領域を超えて適用されるのだ:
流れシステムには2つの基本的な特徴(性質)がある。流れる電流(例えば、流体の熱、質量、情報)と、それが流れるデザインである。たとえば稲妻は、雲から電気を放出するためのフロー・システムである。電流(電気)を体積(雲)から点(教会の尖塔)へ移動させる非常に効率的な方法だからだ。河川の流域の進化も、ある地域(平野)からある地点(河口)へと水を移動させるため、同じような構造を生み出す。また、肺の空気の通り道(酸素の流れ)や毛細血管(血液の流れ)、脳の神経細胞の樹状突起(電気信号や映像の流れ)にも、樹木のような構造が見られる。このような樹木状のパターンが自然界全体に見られるのは、それが効果的なデザインだからである。
木のような構造を探してみよう。そこには、老子が私たちに抵抗するなと警告している流れがある。
私はネットでベジャンと彼の仕事に関する記事を見つけた。泳ぐ魚、走る哺乳類、枝分かれする樹木などだ。当時はあまり気にも留めなかった。私はまだ複雑性の洞察、つまり創発の研究、部分と全体、そしてそれらが生きるルールの関係を統合している最中だった。複雑性の創発とベジャンの言っていることの間に、もっと密接なつながりがあることに私はほとんど気づいていなかった。
あるイベントでJ・ペダー・ゼインというジャーナリストに出会わなければ、私はそのことを見過ごしていただろう。ゼインはベジャン教授と一緒に本を書いていた(上記の一節が掲載されている)。私たちは話をするようになり、やがて興味を共有するために昼食を共にした。いつの間にか、私は自宅に戻り、オンラインでコンストラクタル法を検索していた。
私はすぐに、この新しいレンズを自分の興味に向け始めた。
チャンネルとルール
2010年9月、私は初めてベジャン教授に電話をかけた。私の専門は主に政治・経済理論なので、コンストラクタル法をこれらのテーマにどこまで拡張しているのか知りたかったのだ。私はコンストラクタル法と法的ルール(制度)の関係について尋ねた。結局のところ、もしコンストラクタル法則が自然の法則であり、それは生物であれ無生物であれ同じようにシステムに及ぶのであれば、人間の社会的取り決めにも及ばないのだろうか?
彼は疲れたように、最近エジンバラに行ったときのことを私に話した。ベジャンは学術論文の講演のために徒歩で移動していたのだが、ふとしたきっかけで、その日、彼自身のレッスンを受けることになった。説明を始めると、彼は疲れを癒した。
「人にぶつかってばかりいたんだ。なぜこんなことが起こるのだろう?イギリスの人たちは左側通行なんだ。」
スコットランド人の自然な傾向として、歩行者専用道路という相対的に無秩序な場所で、交通ルールを模倣する。ベジャンは非公式のルールを破っていたのだ。流れをつかむために、彼はエディンバラ人のローカルなチャンネルに適応しなければならなかった。
「チャンネルはルールに似ている」とベジャンは言った。
ベジャンは新しい制度経済学者ダグラス・ノースの研究を読んだことがあるのだろうか。彼は特定の制度(ルール)が “取引コストを下げる “傾向があると述べている。これは結局のところ、経済用語で “フロー “を意味する。
ノーベル賞受賞講演の中で、ノースはこう述べている:
制度とは、人間の相互作用を構造化するために人間が考案した制約である。制度は、フォーマルな制約(規則、法律、憲法)、インフォーマルな制約(行動規範、慣例、自らに課した行動規範)、そしてそれらの執行特性から構成される。
しかし、制度-フォーマルおよびインフォーマル-は、社会の成功にとってどれほど重要なのだろうか。
制度は社会、特に経済のインセンティブ構造を規定する。……制度的取り決めに関係なく、行為者が総所得を最大化する解決策に到達するのは、コストのかからない交渉の条件下においてのみである。取引にコストがかかる場合、制度が重要になる。そして、取引にはコストがかかる。
確かに取引にはコストがかかる。
人々が取引に応じると信じなければならない。取引相手を見つけることができなければならない。規制当局や税務署、賄賂を徴収する強者など、第三者の仲介者が多すぎない、より広いビジネス環境を頼りにしなければならない。ゲームのルールは、長期にわたる経済的繁栄にとって極めて重要である。同様に、システム内のチャネルは、時間の経過とともに形成され、流れを改善する。
脈管形成
かつていたるところで目にしたフラクタルと同じように、私はいたるところでコンストラクタル的原理が働いているのを目にするようになった。ベジャンはこれを “脈管形成 “と呼んでいる。大きな違いは、フラクタルは説明するだけで、コンストラクタル法は説明するということだ。ベジャンはこう書いている:
コンストラクタル法は、自然界に見られるデザインを説明するだけではない。なぜデザインが生まれるのかを理解し、それが将来どのように進化していくのかを予測するために使える法則を明示しているのだ。
脈管形成を理解するために、樹木の形態と機能を考えてみよう。空中で、なぜ樹木は枝分かれするのか?二酸化炭素の流入を確保するためだ。土壌中では、なぜ根はあのように分岐するのか?樹木への養分と水の流入を最適化するためである。樹木が老廃物(酸素)を排出することで、人間の心臓血管系に必要な新鮮な空気が確保される。私たちの血管系は植物のそれと共進化してきたので、植物と人間のシステムが木の枝に似ているのも不思議ではない。
世の中の流れに対応するため、脈管形成が盛んに行われている。河川の流域から牛乳を配達する輸送網まで、あらゆるものに樹木のような構成が見られるのは、ベジャンの原理が働いている例である。このようなシステムが時間的に持続するためには、より良い流れを継続的に提供しなければならない。
コンストラクタル法によって説明または予測される現象
- 森林における樹木の形と分布
- 河川流域の形態と機能
- 循環系の形態と機能
- 動物の飛行の物理学
- 走る動物の物理学
- 泳ぐ動物の物理学
- オリンピック・ランナーの大きさ、形、人種
- オリンピック水泳選手の体格、体形、人種
- 大学ランキング
- 大学バスケットボールランキング
- 少数の大と多数の小
最後に、富の問題にたどり着く: 私たちが自然界のいたるところで目にする樹木のような/血管のようなデザインは、経済、企業、会社、CEO、従業員、投資家、消費者にどのように及んでいるのだろうか?
「コンストラクタル法とは、自然界におけるデザインの生成はすべての物理学の現象であるという考え方である」とベジャンは言う。すべての物理学とは、「生物、無生物、地球物理学的、社会的なすべてのもの 」を含む。これは強力で大げさな主張だが、ベジャンは自信を持っている。彼の法則は、多くのことを説明できる実り多いものだ。
貧富の差を説明できるのだろうか?
ベジャンの共同研究者であるフランスのシルヴィー・ロレンテは、コンストラクタルデザインは “少数大小 “の特性を示すと主張している。つまり、流れシステムは通常、血管系のように組織化され、大きな流れが次第に小さな流れにつながっていく。この法則が複数の領域にわたって成り立つとすれば、大学ランキング、高給の仕事、富のどれをとっても、資源の分配は似たようなパターンを示すことになる。所得の場合、コンストラクタル法は、大きな純資産を持つ少数の人々と小さな純資産を持つ多くの人々がいる理由を説明する。富はスケーリング法則のように、このように自然に分配される。しかし、この分布は宇宙的な事故でもなければ、アレアトワールでもない。進化した分布は機能的である。
機能は形を生み、形は流れを意味する。
コンストラクタル法は、エネルギー使用量とGDPの強い関係を説明する。先進国が豊かなのは、発展途上国よりも効率的にモノを運ぶことができるからだ。エネルギー消費とは、簡単に言えば、物を必要な場所に移動させるための尺度である。それなら、世界最大の企業のいくつかがエネルギーとフローに関係しているのも不思議ではないだろう。
エクソンモービル(エネルギー)、
ウォルマート(物流と小売)、そして
グーグル(情報)である。
起業家は、価値ある製品、サービス、情報を作り、移動させることができる。J.P.モルガンとヘンリー・フォードを思い浮かべてほしい。情報分野では、ジョブズ、メトカーフ、バーナーズ=リーの前に、グーテンベルク、モールス、ベルがいた。
「富はある意味で流れであり、動きであるからだ。富は抽象的なものではない。」
富は物理的な世界とつながっているため、ベジャンはそれが流れる経済の進化したデザインを支えていると考えている。
以上、コンストラクタル法に関するシリーズの第2回をお届けした。第1回はこちら。次回は、富とフローの関係について論じる。
