レックス・フリードマン
チャンネル登録者数 168万人
Stephen Wolframはコンピュータ科学者,数学者,理論物理学者であり,Mathematica,Wolfram Alpha,Wolfram Language,そして新しいWolfram Physicsプロジェクトを運営するWolfram Researchの創設者兼CEOを務めています.個人的なことですが,この本は私がコンピュータサイエンスと人工知能を学ぶ上で最も影響を受けた本の1つです.
Lex Fridman 0:00
コンピュータ科学者,数学者,理論物理学者であり,Mathematica,Wolfram Alpha,Wolfram言語,新しいWolfram physicsプロジェクトを開発したWolfram research社の創設者兼CEOであるStephen Wolframは,「a new kind of science」を含むいくつかの本の著者でもあります.この本は、私がコンピュータサイエンスや人工知能を学ぶ上で最も影響を受けた本の一つです。確かに、スティーブンに対する批判のひとつには、彼が大きなエゴを持っているために、彼のアイデアの内容を十分に楽しむことができない研究者がいるという、人間的なレベルの問題があるかもしれません。
この点については、今回の対談でも話しています。私にとってエゴは、道を誤らせることもありますが、学術機関の慎重なやり方に屈することなく、大胆で革新的な思考を促進するスーパーパワーにもなります。そして特にここでは、私と一緒に人間性の特殊性を乗り越えて、スティーブンスの作品にあるアイデアの美しさに心を開いてほしいとお願いしました。そして、この会話の中で。スティーブン・ウルフラムは、現代で最も独創的な精神の持ち主の一人であり、その核心は、親切で好奇心旺盛で素晴らしい人間であると信じています。
この会話は2019年11月に録音されたもので、Wolfram physicsプロジェクトは進行中でしたが、現在のように一般の人が探究できる状態ではありませんでした。私たちは今、近い将来におそらく複数回、再び話し合うことに合意しました。というわけで、これがラウンド1です。
第2ラウンドの日を楽しみにしていてください。この人工知能ポッドキャストは、YouTubeで購読したり、5つ星やAppleのポッドキャストでレビューしたり、Patreonでサポートしたり、単にTwitterやLex Friedman spelled fri D ma nで私とつながったりして楽しむことができます。それがうまくいくことを願っています。
スポンサーへの広告の簡単なまとめ ExpressVPNとcash app、コードを使用してポッドキャストをサポートすることを検討してください
ExpressVPN ExpressVPN comm slash flex pod and download in cash app and using code Lex podcast. この番組は、cash appが提供しています。アプリストアでナンバーワンのファイナンスアプリを取得する際には、コードLex podcastを使用してください。
キャッシュアプリでは、友人に送金したり、ビットコインを購入したり、株式市場に投資したりすることができますが、その額は文字通り1ドルでした。 キャッシュアプリは端株取引を行うので、端株注文を抽象化するために裏で働いている注文実行アルゴリズムは、アルゴリズム的な驚異であることをお伝えしておきます。
難しい問題を解決し、最終的には株式市場を抽象化した次のレイヤーにステップアップするための簡単なインターフェースを提供したcash appのエンジニアに大きな賞賛を送りたいと思います。これにより、新しい投資家にとって取引がより身近なものになり、分散投資がより簡単になります。
今回も、App StoreまたはGoogle Playからcashアプリを入手し、コード「Lex podcast」を使用すると、10ドルがプレゼントされます。また、Appleは10ドルを、世界中の若者のためにロボット工学とSTEM教育の発展を支援している団体に寄付します。この番組はExpressVPNによって提供されています。ExpressVPN comm slash flex podで割引を受けて、このポッドキャストをサポートしてください。
私は何年も前からExpressVPNを使っています。とても気に入っています。使い方はとても簡単で、大きな電源ボタンを押すだけで、あなたのプライバシーが守られます。お望みなら、世界のどこにでもいるように見せることもできます。
これには多くの明白なメリットがあります。確かに、日本のNetflixやイギリスのwhoaのようなストリーミングサイトの国際版にアクセスできるようになりますし、ExpressVPNはどんなデバイスでも使えます。私はLinuxで使用していますが、Ubuntuには感謝しています。
他にも、ExpressVPN comm slash Lex pod で割引を受けたり、このポッドキャストをサポートしたりすることができます。さて、ここからはStephen Wolframとの会話です。ご子息のクリストファーさんと一緒に、宇宙人の言語や映画「アライバル」の制作に携わったそうですね。少しおかしな質問をさせてください。
もし宇宙人が地球に来たとしたら、私たちは共通の言語を見つけることができると思いますか?
Stephen Wolfram 4:32
宇宙人がやってくると言った時点で、私たちはすでに物語全体に偏見を持ってしまっています。なぜなら、エイリアンが実際に訪れるという概念は、訪れるという話をする上で意味のあるものだということがすでにわかっているからです。つまり、私たちと同じような物理的環境に存在していることがわかっているのです。
単なる無線信号ではありません。それは実際に現れるものなのです。では、人はコミュニケーションの方法を見つけることができるのでしょうか?今のところ、その最も良い例はAIです。つまり、これはエイリアンの知能の最初の例です。
問題は、私たちがAIとどれだけコミュニケーションできるかということです。例えば、あなたがニューラルネットの中にいたとして、それを開いて、「何を考えているの?と話し合うことはできますか?簡単ではありませんが、絶対に不可能というわけでもありません。
ですから、宇宙人がやってくるというご質問の設定を考えると、その時までには、何らかの形でのコミュニケーションを見つけることができると思います。コミュニケーションには目的などの概念が必要です。これは一種の哲学的な泥沼です。

Lex Fridman 5:46
AIが一種のエイリアンの生命体だとしたら、訪問してくるエイリアンはどのようなものだと思いますか?しかし、もしあなたが想像するとしたら、彼は言いました。「訪問する」と言うことで、あなたはすでに何かを予見しています。しかし、宇宙人が訪れるとはどのようなものでしょうか。
Stephen Wolfram 6:09
訪問するということは、このような意味合いがあり、ここでは未来の世界で人間の言葉の不正確さを使っています。もしそれが計算言語で表現されていれば、「visit」という概念を取り上げ、基本的にドキュメントを見て、それが何を意味するのか、どのような特性を持っているのか、などを正確に知ることができるかもしれません。
しかし、普通の人間の言葉で「訪問」というと、何か物理的に具現化されたものがあって、それが宇宙船の中に現れるということだと思っていて、それが必要だということはわかっています。私たちは、ラジオ信号の中に光子が現れて、非常に精巧なパターンになっているだけだとは考えていません。
Lex Fridman 6:58
それはパターンの中の光子になり得るのでしょうか?
Stephen Wolfram 7:01
それはいい質問ですね。つまり、可能性があるかどうか、何をもって知性とするか、ということです。いい質問です。
以前は、地球外知的生命体を発見することの意味が明らかになるだろう、などと考えていましたが、私が行った科学の結果、知的生命体と単なる計算的生命体との間には、いわば明るい境界線はないということがだんだんわかってきました。ですから、日常的な議論の中で、「天気には心がある」などと言います。では、この疑問を解き明かしてみましょう。このように、大気の流体力学を決定する計算プロセスがあることはわかっています。
それを、私たちの脳の中で行われている物理的なプロセスと、どうやって区別するのでしょうか?
どうやって、どうやって、それらを分けるのでしょうか?洗練された計算や天候を表す物理的なプロセスが行われていると、どのように言えばよいのでしょうか?根本的な違いはないと思います。私たちにとっての違いは、異なる脳で起こっていることをお互いに結びつける、いわば歴史の糸のようなものがあるということです。天気に起こることは、文明の歴史の糸ではつながっていないものです。
Lex Fridman 8:30
しかし、天気には独自のストーリーがあるのかもしれません。
Stephen Wolfram 8:38
地球外知的生命体について考えるときには、そこが問題になります。というのも、非常に精巧な電波を発生させているマグニートスフィアというパルサーのように、過去何年、何百万年にもわたって中性子星の中で起こっているプロセスによって発展してきた全体的な文明であると考えるべきなのか、それとも人間の知性に慣れているものと比較して考えるべきなのか。
最終的には、人々が地球外知的生命体の話をするとき、それはどこにいるのか、また、フェルミのパラドックスのように、宇宙には知的生命体の4つ目の兆候がないのはなぜか、ということになると思います。私が思うに、私たちは2つの異質な知性の形を持っていて、人工的な知性と、物理的または地球外の知性を扱っています。
そして、人々はこの2つが同時期に達成されたという事実に慣れていくのではないでしょうか。言い換えれば、人々は、コンピュータや物、私たちが作ったデジタル物が私たちのようにある種の知的であることに慣れていて、宇宙には私たちのようにある種の知的なものが存在するが、私たちのような文明の歴史を共有していない、という考えにも慣れていると言うでしょう。
つまり、私たちが知らない、彼らは彼らで別のブランチなのです。つまり、生命について語るときと似ています。例えば、あなたは、生命体と知性とをほぼ同義に語ったと思いますが、私はそうは思いません、あなたの話を聞くとAIは腹をたてるでしょう。
Lex Fridman 10:19
本当におそらく生物学的な生命を意味しているのでしょう。そうですね。でもあなたは、もっと詳しく調べてみますが、本当にスペクトルだと言っているのですね。そして、それはすべて一種の計算に過ぎないと?つまり、それは完全なスペクトルであり、私たちは特定の種類の計算にまつわる物語を編むことで自分たちを特別な存在にしているだけといことですね。
Stephen Wolfram 10:40
そうですね、私が気付いたのは、あるレベルでは、計算量が少ないことに気付くのは少し憂鬱ですが、それが解放されるということです。まあ、そうなんですが、つまり、これは科学の話なんですよね。そうでしょ?コペルニクスから始まって、最初は自分たちの惑星が宇宙の中心にあると確信していたようなものでした。
しかし、それは真実ではありません。次に、生物としての人間が持つ化学的性質には何か特別なものがあると確信しました。それも本当ではありません。そして、私たちが持っているこの知性というものに、まだ希望を持っています。それは本当に特別なことです。
ええ、そうは思いません。しかし、ある意味では、あなたが言うように、特別なのは私たちの細部であることに気づくという次のような理由で、それはある種の解放感をもたらします。何か他のものがやってくるのではないかと思うような、抽象的な属性ではありません。
そして、その抽象的な属性も持っているということですか?そう、すべての抽象的な属性は、他の何かが持っているものなのです。しかし、私たちの文明の歴史などの詳細については、他の何者も持っていません。他のものにはない、いわば私たちの物語です。
そしてそれは、ほとんど定義上、特別なものです。だから私は、この作品はそれほど特別なものではないと考えています…つまり、最初は「これはダメだ。自分のやっていることにどうやって敬意を払えばいいのか。そして、私たちが行っていることの詳細がすべてのストーリーであり、それ以外はすべて白紙のキャンバスのようなものだと気づいたのです。
Lex Fridman 12:11
ちょっとした余談ですが、彼は私にそのことを考えさせました。
モノリスと『2001年宇宙の旅』について、宇宙人が私たちとコミュニケーションを取り、私たち人間が持っている特殊な知的計算能力に火をつけたという点では、どう思われますか?そこから何か面白いことが得られるのでしょうか?sci fi?
Stephen Wolfram 12:35
モノリスとは、1~4~9個の完全な立方体のことです。100万年前の地球では、猿の群れなどと一緒に存在していました。そのようなレベルの完璧さを持つものは、場違いであり、非常に構築されたものであり、非常にエンジニアリングされたもののように見えます。
これは興味深い質問です。いわば、テクノ・サインとは何か?どこかで目にして、「これは作られたものに違いない」と思えるものは何でしょうか?実際には、私たちは非常に完璧な結晶を目にします。そして、完璧なものはとても完璧です。
多面体でも何でもいいのです。そういう意味では、完璧な多角形や多面体の形をしているというのは、技術的なサインのようなものだと言えるでしょう。それは真実ではありません。有名な数学者であるガウスは、シベリアの森を伐採して、ピタゴラスの定理の証明の典型的なイメージの形を作るべきだというアイデアを持っていましたが、このアイデアは実現しませんでした。しかし、火星人がそれを見て、「ああ、数学者がいるんだな」と気づくだろうという根拠があるのです。彼の世界観では、これが人類の文化的成果の最高の宣伝になったのでしょうね。
しかし、理にかなった質問だと思いますが、何を送り、何を作ることができるのか、それは創造における知性、あるいは創造における意図の表れなのでしょうか?
Lex Fridman 14:21
もし私たちがビーコンを送るとしたら、何を送るべきかというと、私たちの最大の創造物である数学ではないかと話しました。
私たちの最大の創造物は何でしょう?I
Stephen Wolfram 14:31
これは、哲学的に絶望的な問題だと思います。つまり、あなたが何かを送って、それが素晴らしいと思っても、それは私たちが宇宙の一部であるようなものなのです。計算というのは、ある意味で抽象的なものであり、我々が作る精巧なものを作るために使う感覚ですが、これは驚くほどどこにでもあるものです。
言い換えれば、私たちは、マイクロプロセッサにつながる巨大なエンジニアリングスタックを構築して、精巧な計算ができるようになったと考えていたかもしれません。しかし、計算は至る所で行われているという考えは、唯一の問題は、人間の意図とその計算内容を結びつける糸があるかどうかということです。
私たちの文明を最大限にアピールするためには、何を送ればいいのかという疑問があると思います。私たちが作ったほとんど無作為に並べられたものは、すべて等価であるということだと思います。それ以外はすべて。これは、次のような問題のひとつだと思います。
Lex Fridman 15:39
お話の途中で申し訳ないのですが、私はちょうどcrossingの奥さんであるAndrewと話したところです。ボイジャーの「私」に詳しいかどうかはわかりませんが、彼女は「私」の脳波を送信する役割を担っていましたが、それは彼女だけのものではありませんでした。
彼女がカール・セーガンに恋をして、彼の美しい物語を書いていたときの脳波でした。そうですね、おそらく彼は、他の何よりも私たちがそうするかもしれないと言って、その力を封じてしまうでしょう。それは興味深いことで、すべてが興味深い、独特のものです。
Stephen Wolfram 16:17
That’s Yeah, yeah. そうですね。ボイジャーの「ゴールデンレコード」を見ると、ちょっと面白いと思いますよ。これが面白いのは、70年代後半に作られたものだということです。80年代前半?蓄音機のレコードなんだ。
蓄音機レコードの再生方法の図が書いてある。たった30年の間に、今の子供たちにそれを見せて、その図を見せて、実験してみたんですが、これが一体何なのかわからないんです。それが今の私たちのやり方です。たった30年の間に、私たちの技術は、ヒーラー・コール、つまり蓄音機のレコードの機械的なトラックを演奏することが、今では奇妙なことになるまでに進歩しました。
ですから、これは教訓的な話だと思いますが、詳細な情報を提供してくれるものを作る能力という点では、宇宙人などが何かをしようとしても、「いや、最善を尽くしてくれ」という感じです。私が言うように、もし今日これをやるとしたら、針を使ったヘリカルスキャンのようなものは作らず、高解像度の画像処理システムを使って、すべてのビットを取り出し、「ああ、ヘリックスやスパイラルを入れるのは大迷惑だ。螺旋を解きほぐしてみようじゃないか。そして、そこからスタートするのです。
Lex Fridman 17:50
AIの解釈可能性や計算の解釈可能性、様々な種類の計算とのコミュニケーションが可能かどうかを探ることになると思いますか?このレコードを再生するには?
Stephen Wolfram 18:11
それは人が何をしたいかという問題ですね。というか。
Lex Fridman 18:14
相手が伝えようとしていることを理解したり、相手について何かを理解したりすることです。
Stephen Wolfram 18:20
それは何を意味しているのでしょうか?つまり、それが問題なのです。問題は、人々がコンピュータの自然言語理解を行おうとしていたときのようなものですね。何年も前から試みられていたんですね。しかし、それが何を意味するのかは明確ではありませんでした。
言い換えれば、あなたは自分の英語か何かを手に取り、「おや、私のコンピュータはこれを理解している」と言うわけです。よし、それはいいね。これで何ができるでしょうか?例えば、私たちがMalfaを使って構築したときのことを考えてみましょう。
質問応答などを行っていましたが、自然言語理解を行う必要がありました。後になって気づいたのですが、私たちが自然言語理解をうまくできたのに、他の人たちができなかった理由は、第一に、自然言語理解に実際の目的があったからです。
同じように、宇宙人を想像するとき、彼らにレコードを聞かせるとしましょう。彼らはそれを理解しましたか?意味にもよりますが、もし彼らが、もし私たちが、もし彼らが持っている表現があって、それが何らかの表現に変換されて、私たちが「ああ、これは、私たちが認識できる表現で、理解を表している」と言えるのであれば、それは良いことですが、実際には、理解を表していると言えるのは、私たち人間が便利だと認識するようなことをしてくれるものだけです。
Lex Fridman 19:47
この特定の文明がどれだけ技術的に進んでいるかを理解し、定量化しようとしているのかもしれません。
では、軍事的な観点から見た場合、彼らは私たちにとって脅威となるのでしょうか?
ええ、おそらくそうでしょう。私たちが興味を持つであろう最初の理解のようなものは?
Stephen Wolfram 20:03
それはとても難しいですね。ライバルの映画でも、「なぜあなたはここにいるのか」というのが重要な質問のひとつになっていましたね。
Lex Fridman 20:10
そして、それは私たちを傷つけることになります。
Stephen Wolfram 20:12
かなりの痛手になります。しかし、それさえも、非常に不明確です。つまり、AIが私たちを傷つけることになる、ということです。これは、多くの興味深いAI倫理問題に戻ってきます。「あなたを傷つけないようにしたいので、制限速度で正確に運転するようにしましょう」と言うかもしれません。
そして、それはある意味では私を傷つけることになるのです。だから、傷つくとはどういうことなのか、その定義さえもわからないのです。そう、誰かが不明確なのです。そして、AIの倫理などについて考え始めると、それは解決しなければならないことです。
Lex Fridman 20:57
それは常にトレードオフです。それが倫理の厄介なところですね。
Stephen Wolfram 21:00
はい、そうですね。倫理とは、私たちが話している他の事柄と同様に、深く人間的なものだと私は思います。倫理的に正しいことを証明する定理を書こう」というような抽象的なものではなく、それは無意味な考えです。いわば根拠となる真実が必要で、それは究極的には人間が望んでいることなのだと思います。人間は皆、同じことを望んでいるわけではありません。だからこそ、それについて考えることは、あらゆる種類の複雑さを伴うのです。
Lex Fridman 21:27
ジョージアが倫理を計算に変える際に便利なのが、「種の存続の可能性を最大化するものは何か」という問題です。
Stephen Wolfram 21:38
実存的な良い問題ですが、では、種の存続というと、ですね。例えば、テクノロジーのことは忘れて、ハングアウトして、幸せに暮らして、次の世代に引き継いでいく、ゲーテのように、何世代にもわたって、ある意味では何も起こらない、というようなことです。
そうですか、そうではありませんか?わかりにくいのですが、精巧なことをやろうとすると、その試みは種の存続には逆効果になるかもしれませんよね?例えば、私が思うに、それはまた、少しわかりにくいことです。生き延びるために必要な脅威は何かというと、超巨大火山、小惑星の衝突、その他あらゆる種類のものがあります。
そして、これらの脅威に対して、私たちの種をできるだけ強固なものにしましょうと言うのです。最終的には、何が、何が必要なのか、それはわからないことだと思います。長期とは、太陽が燃え尽きるまで、という意味でしょうか?それではうまくいきません。
これは、もしあなたが会社を経営しているとしたら、ある一定の期間、会社を非常に安定させることができるようなものです。例えば、もしあなたの会社がどこかの民間投資グループに買収されたとしたら、彼らは、会社がやっていることをそのままにして、すべての研究開発を排除することで、5年間は会社をうまく運営することができます。
もしAIに、人間は1000年は大丈夫だと言った場合、それを最適化するためにやるべきことは、おそらく決まっているでしょう。しかし、最終的には、この問題を考え始めると、決定不可能性、計算の非簡約性がずらりと並んでいることに気づくと思います。
言い換えれば、私たちの文明が経験してきたこと、そして私たち人間が経験してきたことの良い点の一つは、ある種の計算の不可解さがあるということです。つまり、外から見て「答えはこうだ」と言えるようなものではなく、最終的には「こうなる」ということを、実際にプロセスを踏んで見つけなければならないのです。
そのほうが、ある意味では気持ちがいいと思います。このようなプロセスを経ることで何かが達成されるということではなく、AIに伝えることで、何が最良の結果になるのかを考えに行くということです。残念ながら、AIは何をすべきかは決定できないと言ってくるでしょう。
どうなるかを確認するためには、すべてのシナリオを実行しなければなりません。また、それを無限の未来に向けて実行しようとすると、すぐに無限会社の標準的な問題に直面することになります。そういったことです。
Lex Fridman 25:01
宇宙の答えを見つけて、すべてが42であったとしても、実際に宇宙を運営しなければならないということですね。そうですね。疑問というか、旅は重要ですよね。
Stephen Wolfram 25:17
まあ、要約すると、これは宇宙の結果だ、ということだと思います。それが可能であればの話ですが。つまり、計算などについて考えたり、物事がどのように機能するかについて考えるための、全体的な構造を教えてくれているのです。
もしも、もしも、それが可能で、その答えがこんなものだとしたら、基本的には、宇宙の外に出る方法があると言っていることになります。そして、あなたは一種のパラドックスに陥っているのです。なぜなら、もし答えを知ることができるなら、宇宙が提供するものを超えて、それを知る方法があると言っているからです。
しかし、もしそれを知ることができるのであれば、私たちが扱っている何かは宇宙を超えていることになります。そうなると、いわば宇宙は宇宙ではないということになります。
Lex Fridman 25:59
一般的に、少なくともはるかに小さい人間の脳の話をすると、十分に複雑な計算の結果を示すのは難しいですね。つまり、おそらく不可能なんですね、決定不可能性。つまり、少なくとも詩人の目には、宇宙は十分に複雑であると映っていて、いったい何が起こるのかを予測することはできないということでしょうか。
Stephen Wolfram 26:30
予測できない方がいいですね。予測できたとしても、それはつまり、宇宙の奇妙な部分にあることを否定しているようなものですからね。そうですね。では、私たちが予測するということはどういうことかというと、私たちの小さな宇宙の一部が、宇宙全体よりも先にジャンプできるということです。
予測が可能になる唯一の方法は、私たちが宇宙の中でとても特別な存在であり、宇宙に存在する他の何よりも特別で洗練された計算が存在する場所である場合です。そうでなければ、宇宙で起こることを予測する、いわば神学的な能力を持つことはできません。それは、私たちが宇宙の他のすべてのものよりも優れていると言いたいのでしょうが、そうではないと思います。
Lex Fridman 27:16
宇宙全体で繰り返される多数のループパターンを検出し、それらを完全に記述することができるかもしれませんが、しかし、それらのパターンがどのように相互作用するのかを見ることは非常に困難です。そして、どんな風にうまくいくのか。
Stephen Wolfram 27:33
宇宙の最も注目すべき点は、規則性があるということですが、もし、ただ単に
Lex Fridman 27:41
規則性とは
Stephen Wolfram 27:42
絶対にあります。物理学は成功していて、宇宙がどのように機能しているかを詳細に教えてくれる法則がたくさんあります。つまり、宇宙にある19個の粒子のうち、10個目の粒子がそれぞれの役割を果たすということもあり得ます。しかし、実際にはそうではありません。
すべての粒子が基本的に同じ物理法則に従っています。これは宇宙に関する非常に深遠な事実です。そこからどのような結論を導き出すのかは不明です。
つまり、初期の神学者たちは、神の存在を示す一番の証拠としていたのです。今では、人々はそれについて異なる結論を出しています。しかし、実際のところ、私は今、たまたま基礎物理学に興味を持っていて、それを再開したところです。物理学の基礎理論を実際に見つけられるかどうか、ちょっとした探求をしているんです。
Lex Fridman 28:41
素晴らしいですね。その話になりますね。なぜなら、物理学の観点から私たちの現実の基本的な性質について、あなたは魅力的な見解を持っていると思うからです。さて、一歩下がって考えてみましょう。
計算とは何でしょうか?
Stephen Wolfram 29:09
いい質問ですね。操作上、計算とは規則に従うことです。そんな感じですね。つまり、計算とは規則に沿って体系的に行われたプロセスの結果なのです。そして、それを実行したときに起こることなのです。
Lex Fridman 29:24
初期条件を設定し、入力を行い、ルールに従うということは、何に対してルールに従うのでしょうか?つまり、何かデータがあるはずなのです。
何か?
Stephen Wolfram 29:34
必ずしもそうではありません。非常に単純な入力があって、そのルールに従うということもあります。望むならば、初期条件をルールの中に詰め込むことができるからです。
そこで問題になるのが、「計算」という概念にロバスト性はあるのか、ということです。つまり、これは何を意味するのでしょうか?私が言いたいのは、こんな感じです。
エネルギーのように、さまざまな形のエネルギーがありますが、エネルギーは、運動エネルギーや核エネルギーなどに特化したものではなく、確固とした概念があります。では、「計算」という概念は強固なものなのでしょうか。あるいは、この計算がチューリングマシンで実行されているかどうか、CMOSシリコンCPUで実行されているかどうか、流体システムで実行されているかどうか、そのようなことが問題になるのでしょうか?なるほど。
それは公平なのでしょうか?そうですね。つまり、あることが明らかではなかったのです。ですから、どのようにして今の状況に至ったのか、その歴史を理解する価値があります。なぜなら、「ある」と言うことは、私たちの宇宙についての一つの声明であり、数学的に考えられることについての声明ではないからです。数学的に考えられることを言っているのではなく、私たちにとって実際に存在しうることを言っているのです。
Lex Fridman 31:03
エネルギーというのは、概念としてはしっかりしています。粒子に力を与える粒子、質量を持つ粒子に力を与える粒子など、この種のアイデアは、少なくとも数学的な意味では、互いに対応しているように見えます。エネルギーや質量と計算には関連性があるのでしょうか。
それとも、これらは全く別の考えなのでしょうか?
Stephen Wolfram 31:44
それはまだわかりません。私が基礎物理学についてやろうとしていることは、そのような関連性につながるかもしれませんが、現時点では既知の関連性はありません。
Lex Fridman 31:54
では、もう少し詳しく教えてください。
あなたは計算についてどのように考えていますか?計算とは何でしょうか?
Stephen Wolfram 32:02
つまり,少し歴史的な話をしましょうか。そうですね。150年前にさかのぼると、人々は様々な種類の機械式計算を作っていました。典型的なものは、加算器が欲しいなら加算器屋に行き、基本的には乗算器が欲しいなら乗算器屋に行く、というように、さまざまなハードウェアがありました。
つまり、少なくともその種の計算とその種のハードウェアのレベルでは、強固な計算の概念は存在しないということです。加算機のコードを使った計算と、乗算機の複雑な概念を使った計算があります。それらはバラバラなのです。1900年頃に何が起こったかというと、人々は想像し始めました。
特に数理論理学の文脈では、どんな合理的な機能も表現できるようなものができないだろうか、と。プリミティブ・リカーション(原始再帰)はその初期のアイデアの1つでしたが、うまくいきませんでした。原始再帰のプリミティブを使っても表現できない合理的な関数が存在していたのです。
さて、1931年になって、ゲーデルの定理などが出てきました。振り返ってみると、ゲーデルの定理を確立する過程で、ゲーデルは基本的に、いかにして算術を組み立てるか、いかにしてこの文は証明できないといった論理的な文を算術に組み立てるかを示しました。
つまり、彼が本質的に行ったことは、算術は、他のあらゆる種類のものを表現することができる、ある意味でコンピュータになり得るということを示したのです。そして、936年にチューリングが登場し、チューリング・マシンを開発したのである。
一方、アロンゾ・チャーチはラムダ計算を考え出しました。そして、非常に早く確立された驚くべきことは、計算とは何であるかについてのチューリングマシンの考えは、計算とは何であるかについてのラムダ計算の考えと全く同じであるということです。
その後、レジスター・マシンや他の種類の計算の表現方法など、他のアイデアが出てきました。そして大きな驚きは、それらがすべて等価であることがわかったことです。言い換えれば、昔の加算機や乗算機のように、チューリングにはチャーチの計算のアイデアがあり、チャーチには計算のアイデアがあったのかもしれません。
そして、それらはただ違っていたのです。しかし、そうではありません。実際にはすべて等価なのです。その後、1970年代くらいまでに、計算、コンピュータサイエンスの計算理論の分野では、「チューリングマシンは計算の一種である」と言われるようになりました。しかし、物理学者たちは、「いやいや、そんなことでは宇宙は動かない。微分方程式があり、無限の桁数を持つ実数がある。」と。
Lex Fridman 34:43
宇宙はチューリングマシンではありません。
Stephen Wolfram 34:45
チューリング・マシンは、マイクロプロセッサーや工学的構造などで作られるもののごく一部ですからね。1980年代に計算と物理学モデルの関係を研究したことで、物理学で起こりうることと、チューリング・マシンのようなものとの間に大きな二項対立があるということが、少しずつ明らかになってきました。
そして、おそらく今では、人々はほとんど、「ところで、脳はこの問題の別の要素だ」と考えているでしょう。つまり、ゲーデルは、彼の計算の概念、あるいは彼の計算の概念に相当するものが、脳をカバーするとは考えていなかったのです。チューリングも確信はありませんでした。
しかし、彼は少しずつですが、脳をカバーするべきだと確信するようになりました。しかし、1980年代のある時期までには、チューリングマシンのようなものが捉えることのできる計算の概念は、それなりに強固なものであるという一般的な信念が生まれ始めていたと言えるでしょう。
さて、次の問題は、あらゆるチューリングマシンができることを何でもできるようにプログラム可能な、普遍的なチューリングマシンができるかどうかです。普遍的な計算というのは重要なアイデアで、1つのハードウェアを持ち、異なるソフトウェアでプログラムすることができるというアイデアです。
これは、現代のほとんどのテクノロジーを立ち上げたアイデアのようなものです。つまり、コンピュータ革命やソフトウェアなどを立ち上げたアイデアなのです。普遍的なコンピュータを作ろうとすると、100万ゲートのマイクロプロセッサを用意しなければならず、そのレベルの計算技術を達成するためには大変な苦労をしなければならないようなのです。
私が驚いたのは、80年代初頭に発見したセルラー・オートマトンと呼ばれる非常に単純な計算システムでした。驚いたのは、ルールが非常に単純な場合でも、ルールがはるかに複雑な場合と同じくらい洗練されたことをしていたことです。つまり、「高度な計算をするためには、非常に高度なルールを持ったものを作らなければならない」という考えは成り立たなかったのです。
それどころか、高度な計算は、信じられないほど単純なルールを持つシステムでさえ、完全にユビキタスに存在していることがわかったのです。つまり、何らかのルールに従っているシステムがあるとき、そのシステムがある意味で明らかに単純なことをしていないときは、そのシステムの動作に対応する計算は同等の洗練されたものである、ということです。
つまり、想像できる限りの非常に単純なものから、あっという間にある種のしきい値に達し、それを超えるとすべてが等価となり、その計算の精巧さは明らかではなくなります。つまり、それは科学的な事実なのです。そうですね。
Lex Fridman 38:10
ちょっと待ってください。あなたはこのようにして、新しい種類の科学で幕を開けたのです。私は、とても目からウロコだったことを覚えています。こんなにシンプルなものが、こんなにも複雑なものを生み出すのかと。そして、確かに等価性はあるのですが、それは事実ではありません。
つまり、これらの理論が非常にエレガントであるという事実と同じくらい、事実のように見えるのです。それは、物事がそうであるように見えるということです。でも、ちょっとお聞きしたいのですが、先ほど、コンピュータ科学者のコミュニティにはチューリングマシンがあり、物理学者のコミュニティには宇宙があり、そして誰でもいいのですが、脳を研究している神経科学者もいますよね?この同等性について、あなたはどのように感じていますか?あなたは自分の研究を通して示しましたか?単純なルールは、等価に複雑なチューリングマシンシステムを作ることができる、ということですね。
宇宙はチューリング・マシンの種類と同等なのでしょうか?人間の脳は?チューリング・マシンの一種ですか?それらは基本的に融合しているのでしょうか?それとも、どのようにしてそこに接合しているのか、まだ謎があるのでしょうか?
Stephen Wolfram 39:25
まあ、私の推測では、それらは溶け合うだろうと思いますが、それを確実に知ることはできません。しかし、私は、「計算等価性の原理は、ある種の科学的事実である」と軽々しく言ってしまいましたが、私が中途半端な言葉を使っていなければ、そう、科学的事実のための努力です。問題は、それが複雑な認識論的性格を持っているということです。
熱力学の第二法則やエントロピーの法則のようなものと同様に、熱力学の第二法則とは何なのか?
それは自然の法則なのでしょうか?それは物理的世界に当てはまることなのでしょうか?そうですか?数学的に証明可能なものでしょうか?それは、私たちが見ている世界のシステムに、たまたま当てはまることなのでしょうか。
それはある意味で、熱の定義かもしれません。それは、これらの要素が組み合わさったものです。計算等価性の原理も同じです。ある意味では、計算等価性の原則は、計算の定義の核心でもあります。なぜなら、すべてのシステム間で等価であり、個々のシステムの詳細に依存しない強固な概念が存在することを示しているからです。
だからこそ、「計算」というものについて意味のある話ができるのです。私たちは、「ああ、この計算とチューリングマシン番号3785、などなど」という話に囚われているわけではありません。だからこそ、このような強固な概念があるのです。
さて、一方で、計算等価性の原理は証明できるのでしょうか? 数学的な結果として証明できるのでしょうか?答えは、「非常に単純なルールを持つランダムなシステムを投げてください」というものですが、これに沿った素晴らしい結果が得られています。
いくつかのケースでは、あるタイプの想像できる最も単純なルールでさえも普遍的であり、計算等価性の原理から期待されることに従っていることがわかっています。これは、計算の同等性の原理を証明する数学的な証拠の一つです。
Lex Fridman 41:28
その点についてはまだ同意できますか?単純なルールで、複雑な行動を作り出す。しかし、この動作が複雑であることを数学的に示す方法はあるのでしょうか?閾値を超えるとおっしゃっていましたよね。
Stephen Wolfram 41:47
ですよね?それがいろいろな指標になるのでしょうか?例えば、普遍的な計算ができるかどうか、つまり、システムの初期条件が存在し、素数の計算や円周率の計算など、やりたいことを何でもできるプログラムを本質的に表現できるかどうか、ということです。
そうですよね?それが指標となるわけですね。いくつかの例でわかっているのは、そう、その特性を持つと考えられる最も単純な候補は、その特性を持っているということです。これは計算の同等性の原則が示唆するところでもあります。しかし、この計算等価性の原則は、物理的な世界にも当てはまるのかという疑問があります。
チューリング・マシンやセルラー・オートマトンなど、私たちが考え出したあらゆるものに当てはまるのでしょうか?それは私たちの実際の物理的世界に当てはまるのでしょうか?それは、脳みそにとっては正しいのでしょうか?物理的世界の一要素である脳についてはどうでしょうか?はっきりとはわかりません。
そしてそれは、明確な答えが得られるタイプの質問ではありません。なぜなら、これは、ある種の科学的帰納法のようなもので、「これらすべての脳には当てはまるが、ここにいる人は本当に特別で、彼らには当てはまらない」と言うことができるからなのです。
そんなことはあり得ないのですが、もし最終的に物理学の基礎理論を手に入れて、それが例えば単純なプログラムに対応することが分かったらどうなるでしょうか。
そうなると、物理学は基本的に数学の塊になってしまいます。つまり、今の物理学では、「これが理論で、これがルールで、ここではこれが適用される」というようなことはありません。しかし、ブラックホールのすぐそばでは、このルールは適用されず、別のものが適用されているのかもしれません。
そして、私たちが剥がさなければならない玉ねぎの別の部分があるかもしれません。しかし、もし私たちが、「これが物理学の基本理論だ」というところまで到達できたとしたら、それは素晴らしいことです。しかし、もはや、誰かがやってきて、「おっと、チューリングマシンについてはいろいろ書いているが、物理的な宇宙については間違っている、物理的な宇宙で起きていることについては、ある種の基本的な真実がある」と言うことはできません。
私は、物理学の基礎理論を研究するプロジェクトを再活性化しようとしているところです。今日の時点では、何かを見つけることができるのではないか、そして、その意味で宇宙が本当に計算可能であることを確認することができるのではないかと、とても楽観的に考えています。
しかし、私たちはいわば宇宙に賭けているわけですから、わかりません。想定外の動作やバグがあるかもしれませんが、基本的には宇宙のために何があるのかを知っているのです。私は、いわばそのような立場にはありません。
Lex Fridman 44:54
物理学の基本的な法則は、どのような計算から生まれてくるとお考えですか?あなたは、アトミカを売ることができるような、離散的な種類の計算について、魅力的な仕事をたくさんしてきましたね。この非常にきれいな構造は、単純なルールが膨大な複雑さを生み出すことを示す素晴らしい方法です。しかし、物理学の法則を作り出すような計算を記述するには、もっぱら自律的で、十分に一般的なものであると言えます。
Stephen Wolfram 45:39
まあ、そうですね。これは少し複雑な問題です。というのも、普遍的な計算ができるようになると、原理的には何でもかんでも何かでシミュレートできるようになりますが、それは自然なことではありませんよね。あらゆる可能なプログラムが存在する計算世界の中で、可能なプログラムを探して私たちの物理的宇宙を見つけようとした場合、私たちの宇宙に対応するものは、その計算世界を探せば見つかるような小さくて単純なものなのかと問われれば、それが実現可能であるためには、いわば正しい基礎が必要であり、計算を記述するための正しい言語が必要なのです。
そこで私が長い間興味を持っていたのが、「計算で作ることのできる最も構造的な構造は何か」ということです。言い換えれば、セルラー・オートマトンとは、グリッド上に配列されたたくさんのセルを持っていて、すべてのセルが特定の時間に同期して更新されるというものです。
これは非常に特殊で、非常に厳密なものです。しかし、私が思うに、物理学で空間や時間といったものを見るとき、空間や時間の下にあるものは、可能な限り構造を持たないものであり、例えば物理的な空間として私たちが目にするものは、その下にある恣意的に構造を持たないものから来ているのではないかと思います。
私は長い間、最も構造的な構造とは何かということに興味を持っていました。実際、私が昔から考えていたのは、グラフやネットワークを使うことでした。空間とは何か?という質問がありました。例えば、量子力学の初期には、「他のすべてのものが離散的であることを発見したのだから、空間は離散的になるに違いない」と言われましたが、物理学ではうまくいきませんでした。
今日の物理学では、空間はユークリッドが想像したように、常に連続的なものとして扱われています。ユークリッドが最初に言ったことは、「点とは、部分を持たないものである」ということです。言い換えれば、任意に小さい点があるということです。
点の位置には連続性があります。問題は、それが本当なのかということです。例えば、空気や水などの流体を見ると、「連続した流体だから、注ぐこともできるし、あらゆることを連続的に行うことができる」と言うかもしれません。
しかし、実際には、その物理学的性質を知っているので、連続体のように振る舞っているのは、跳ね回っているバラバラの分子の集まりであり、全体としては、連続体のように振る舞っているということがわかります。
そのため、既存のフレームワークや物理学ではうまくいかなかった宇宙でも、その可能性はあると思います。しかし私は、空間の下に、そして時間の下に、もっと構造のないものがあると想像できるかどうかに興味を持っています。
そして問題は、それが計算可能かどうかということです。つまり、いくつかの可能性があるということです。それは計算可能で、チューリングマシンと根本的に同等である可能性があります。あるいは、基本的にはそうではないかもしれません。では、どうしてそうでないのでしょう?そうでない可能性は?つまり、チューリング・マシンは基本的に整数や整数レベルを扱うのですね?そして、ある数に1を加えたり、このようなことをすることができます。
Lex Fridman 48:52
また、彼が何をしたかを保存することもできます。
Stephen Wolfram 48:54
そう、無限の記憶装置を持っているからです。ストレージです。しかし、物理学、あるいは理想化された物理学や理想化された数学をやろうと考えたとき、実数、つまり無限の桁数を持つ数字、絶対的に正確な数字を扱うことができます。誰かが「この数字を取って、それを自分で掛けることができます」と言うことができます。
あなたは無限大に慣れていますか?
Lex Fridman 49:17
この文脈で、あなたは無限大に慣れましたか?計算の文脈では、とてもうまくいっていますか?無限大は重要な役割を果たしていると思いますか?
Stephen Wolfram 49:24
無限大の役割は複雑だと思います。無限大は物事を概念化するのに役立ちます。実際にそれは定義によって目に見えるものではありませんし、ほとんどの場合,目に見えるものではありません。
Lex Fridman
しかし、物理法則の根底にあるかもしれないものの中に、無限大が含まれていると思いますか?
Stephen Wolfram
物理学についての質問には、必然的に無限大が含まれるものが多いと思います。例えば、「光よりも速い旅行は可能か?」という問いに対して、「物理法則があれば、任意の大きさでも、無限に大きくても、光よりも速い旅行を可能にするものを作ることができる」と言うことができますが、そうすると、一種の理論的な問題として無限を扱うことになります。
しかし、空間と時間の下には何があるのか、どうやって計算のインフラを作ることができるのか、という話になりますね。1つの可能性としては、計算インフラ、つまりチューリングマシンのようなものは作れないということです。正確な実数を扱わなければなりませんが、偏微分方程式を扱うと、分離した点に任意に近い正確な実数が存在し、永遠に続く連続体が存在します。
そして、それはあなたが自然について何かをしようとするときに負うリスクであり、あなたが間違っているかもしれないということなのです。そうではなくて、私にとっては、個人的には、ちょっと不思議なことなんです。私は自分の人生の多くを、誰も気にしないようなことができるテクノロジーの構築に費やしてきました。
しかし、その意味では、自分の技術を構築し、それを実行するという意味では、ある種の間違いではありません。しかし、宇宙の基本的な計算インフラが何であるかという問題は、ある意味では必然だと思います。
つまり、かなり抽象的なものになるのは避けられないのではないでしょうか。なぜなら、3次元の空間があり、電子やミューオンがあり、クォークがあり、これがあるというようなことをすべて理解しようとするならば。宇宙のモデルが単純なものであれば、それぞれのものにコードのラインがあるということにはならないでしょう。ミューオンのケースやタウレプトンのケースなどもありません。
Lex Fridman 51:39
これらはすべて創発的なものでなければなりません。だからもっと深いものでしょうか。
Stephen Wolfram 51:42
ええ、つまり、ある種の必然性があるということですが、実際に根本的な構造の構造が何であるかを語るのは少し難しいですね。
Lex Fridman 51:51
あなたは人間には、これらの法則が生まれるような単純な構造を理解するための認知能力があると思いますか?
Stephen Wolfram 52:01
つまり、私は今、この問題の真っ只中にいるということです。そうでしょ?この人間は、起こっていることを理解するのに苦労していますが、理解することで何が起こるかというと、人はウェイポイント(道標)を構築します。つまり、21世紀の現代数学を理解するには、5万年前に数えることが発明された時にさかのぼって数えることから始めましょう、と言ったとします。
それはとても難しいことです。しかし、私たちはより高いレベルの理解に到達するための道しるべを築くことができます。これと同じことが言語でも起きています。何かのために言葉を発明すると、それが認知的なアンカーのようなもの、つまり道しるべとなって、ポッドキャストなどで「これはあるもので、このような本があります」「このような本があります」と説明することができます。
しかし、ポッドキャストという言葉ができて、人々がそれを社会的に理解するようになると、その上に構築していくことができるようになります。これは科学の世界でも同じことが言えると思います。つまり、科学とは、何かを理解するための認知的なメカニズムを見つけて、その上に構築していくという、ある種のウェイポイントを構築することなのです。もし、砂の上からコンピュータまでの道のりを歩かなければならず、その間には何の道もないとしたら、私たちは破滅してしまいます。
Lex Fridman 53:33
まあ、最終的には、賢い類人猿が抽象的な抽象概念を構築するのに十分な能力を持っていれば、苦しむことになるかもしれませんが、最終的には、砂地からコンピュータにたどり着きますよね。ただ、より長い旅になるかもしれません。
Stephen Wolfram 53:44
問題は、あなたが尋ねた「人間の脳は、引用することで、何が起こっているかを理解するでしょうか」それはまた別の問題です。なぜなら、そのためには、人間が理解できる物語を構築するための、ある種のステップが必要になるからです。私はそれが可能になるのではないかと期待しています。とはいえ、文字通り、今日現在、私に言わせれば、よくわからないことに直面しています。
Lex Fridman 54:16
そして、これは、計算が機能するためのルールを理解しようとする、計算の中の小さなパターンなのです。このような生物がどのような種類の計算で自分自身を理解できるのか、興味深い可能性があります。
Stephen Wolfram 54:31
私の推測では、これまで私たちは計算の再構成不可能性についてあまり話してこなかったと思います。しかし、それはこの計算等価性の原則の結果です。つまり、計算中に、すべてのステップを実行して何が起こるかを見るだけで、その計算で何が起こるかを理解できるのかという疑問です。
それとも、先回りして、実際に起こる前に何が起こるのかを把握する、より賢い何かを持つことができるのか。伝統的な科学の多くは、このような計算の非簡約性を追求してきました。つまり、この方程式があれば、それを解けばいいのです。そして、何が起こるのかを理解することができます。
すべてのステップをトレースする必要はなく、方程式を解くことで先に進むことができるのです。さて、計算量等価性の原則の結果として、多くのシステムが計算量的に還元できないということになります。つまり、何をするのかを知る唯一の方法は、それぞれのステップをたどって何が起こるかを見ることです。
なぜでしょう?もし、私たちが、私たちの頭脳を持っているなら、私たちはもっと賢いので、小さなセルラー・オートマトンのように、すべての細胞を調べて更新するようなことをする必要はありませんが、頭脳の力を使って先に進むことができます。
しかし、計算等価性の原則が正しければ、それは正しくないでしょう。なぜなら、私たちが計算をしているのと、私たちの脳が小さなセル・オートマトンをして、その計算をしているということになるからです。計算等価性の原則では、この2つの計算は基本的に等価であるとされています。つまり、私たちはセル・オートマトンより賢くないと言って先に進むことはできないということです。
Lex Fridman 56:11
再現性はとても魅力的です。しかし、これは本当に力強いアイデアです。これは気の毒でもあり、屈辱的でもあると思います。しかし、私たちが物理学の基本的な法則について話している問題は、ある意味で逆の問題です。そのためには宇宙を動かす必要があります。
しかし、「どのような法則が私を生み出す可能性があるのか」を理解することができますか?
Stephen Wolfram 56:13
それは理解できますが、問題は、それが正しいかどうかを知るためには、何らかの計算の非簡約性がなければならないということです。私たちは宇宙に組み込まれているわけですから、宇宙を理解したかどうかを知る唯一の方法が、宇宙を動かすことだとしたら。
宇宙が146億年も動いていたからといって、私たちがそれを実行することはできません。いわば、やり直しがきかないのです。ですから、「はい、そこに電子があると認識できます」と言えるだけの計算の再利用性があることを期待するしかありません。
私は、これは計算の再利用不可能性の特徴だと思います。これは数学的な特徴のようなもので、還元可能なポケットが常に無限に存在しているということです。それらが適切な場所に配置されているかどうか、また、それらに基づいて理論を構築できるかどうかは不明です。
しかし、宇宙と同じもので作られた宇宙の観測者である私たちが、いわば非簡約性のポケットに頼って宇宙を解明できるかどうかという点については、そのように考えています。非簡約性のポケットがなければ、それはうまくいかないでしょう。しかし、私はこの観測者の動作に関する問題を考えています。
この100年間の科学の特徴の1つは、観測者についてより現実的になるたびに、科学について少しずつ学ぶことができたことです。例えば、相対性理論では、観測者は何が何と同時かを知ることができず、光の信号が届くのを待って同時かどうかを決めなければなりません。
だからこそ、熱力学の第二法則やエントロピー増大の法則などが機能するのです。個々の分子を見ることができれば、熱力学的な結論を出すことはできないでしょう。つまり、これらの分子はすべて、ある特定のことをしているだけだと結論づけてしまうのです。
ですから、私が持っている理論では、私たちが経験したことを実際に対応させるためには、観測者の計算やその他の側面について、より現実的なものにしなければならないと強く思っています。私は今、量子力学がどのように機能するかについて、ちょっとした理論を持っています。これは、人間の意識の糸のようなものが、宇宙で観察されるものとどのように関係するかについての、非常に素晴らしく奇妙なアイデアです。しかし、これはその内容を説明するためのいくつかのステップなのです。
Lex Fridman 59:08
量子力学の下位レベルでの観測者の混乱についてはどう思われますか?教科書的な定義である量子力学の下位レベルでの観察者とは? 量子力学では、実際に存在する世界と観察される世界との2つの世界があるとされていますが?そうです。
それをどのように理解していますか?
Stephen Wolfram 59:29
私たちが最近持っていた考えは、実際にはこの問題に当てはまらないかもしれません。それは、まだわかりません。つまり、これは混乱しているということなんです。興味深いことに、私が30年前に話し始めたこれらのモデルを人々が見ると、「いやいや、そんなことが正しいはずがない」と言うのです。
では、量子力学はどうなのか?でしょう?「量子力学の本質とは何なのか、何を再現してほしいのかを教えてください」と言います。いわば、自分が量子力学を持っていることを知るために?この質問は、実際には非常に実用的なものです。というのも、私たちは量子コンピューターを使って様々なことを行ってきました。
「量子コンピュータを持っていて、あなたのAPIに接続しましょう、」と言う会社があります。そして実際に動かしてみましょう。すると、「それはまだやめておいたほうがいいんじゃない?」私たちはまだ準備ができていません。私がずっと気になっていたのは、もし私が量子コンピューターと5分間話したとして、それが本当に量子コンピューターなのか、それとも相手側のシミュレーターなのか、どうやって見分けることができるのかということですが、それは本当に難しいことなのですか?知性とは何か、生命とは何か、といった多くの疑問を解決することはできません。
生命とは何か?
量子コンピューターのテストですか?
その通りです。そのとおりです。「あなたは本当に量子コンピューターなのか」ということです。そして私は、シミュレーション、つまり「Yes」だと思います。それは単なるシミュレーションなのか?それとも、あなたと同じように、本当に量子コンピュータなのでしょうか?
しかし、このように、量子力学の数学的な構造に関する問題と、私たちが明確なことが起こると考えている経験とは、まったく別のものです。しかし、量子力学では、明確なことが起こるとは言っていません。量子力学は、さまざまなことが起こるための振幅の問題です。しかし、私たちの意識の糸は、確定的なことが起こっているかのように動作しています。
Lex Fridman 1:01:21
この点についてもう少し詳しくお聞きしたいのですが、すべてのものの根底にある構造について、グラフの構造のようなものがあるのではないかという考えを述べられていますが、なぜノードとエッジのグラフ構造があると直感したのか、それが何を表しているのかを詳しく説明してください。
Stephen Wolfram 1:01:41
そうですね。さて、質問は、ある意味で、想像できる最も構造的な構造は何かということです。それで、実際、私が最近気づいたのは、去年くらいから、新しい最も構造的な構造を持つようになったということです。
Lex Fridman 1:01:58
ところで、この質問自体が美しいものであり、それ自体が強力なものでもあります。ですから、答えがなくても、質問があるだけで、本当に強い質問なのです。
そうですよね?でも、あなたの新しいアイデアは何ですか?
Stephen Wolfram 1:02:09
ハイパーグラフに関係していますね。基本的には?私が今持っているモデルで面白いのは、計算で起こったことと少し似ていて、私が「ああ、モデルはこれかもしれない」と思っていたものが、それと同等のものを発見したことです。これは非常に心強いことです。というのも、「じゃあ、Trivalent Graphsを見てみようか」ということになるからです。Trivalent Graphsとは、各ノードに3本のエッジがあるグラフのことです。
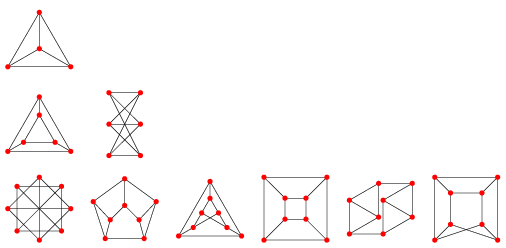
あるいは、特殊なグラフを見ることもできるし、このような代数的な構造を見ることもできる。そして、私が今見ているものは、私が想像していたものの中で、もっともらしいタイプの構造、つまり構造がこれと同等であることがわかりました。では、それは何か?典型的な考え方としては、例えば、数字のタプルの集まりが あるとします。
例えば、135234個の小さな小さな数字の集まり、3つの数字、4つの数字、2つの数字などがあります。そして、これらのある種の浮遊する小さなタプルがあります。順番は決まっていません。そのような浮動的なタプルの集まりです。そして、これは宇宙全体を表す抽象的なものだと言いましたが、それらを関連付ける唯一のものは、記号が同じであるときです。
いわば「同じ」ということです。つまり、2つのタプルがあって、それらに同じシンボルが含まれていて、例えばタプルの同じ位置、タプルの最初の要素に含まれていれば、それは関係を表していることになります。さて、それではこれを元に戻してみたいと思います。なるほど。
これは抽象的だと言いましたが、これは
Lex Fridman 1:03:58
これはこれで、関係は同一性の同じいくつかの側面によって形成されています。
Stephen Wolfram 1:04:03
でしょうか?しかし、しかし、グラフの観点から考えてみましょう。グラフはノードの束で、各ノードに番号を付けるとしましょう、ではグラフとは何でしょう?グラフとは、このノードは他のノードに接続するエッジを持っているというような、ペアのセットのことです。
つまり、グラフとは「このノードは他のノードに接続している」というペアを集めたものなのです。これはそれを一般化したものです。ペアの代わりに、任意のタプルを持つことになります。これが全てです。これですべての話が終わりました。さて、問題は、これが宇宙の状態を表しているのではないかということです。
宇宙はどのように進化しているのか?宇宙は何をしているのか?その答えは、私が見ているのは、これらのハイパーグラフの変換ルールだということです。言い換えれば、「このハイパーグラフの一部がこのように見えるときは、それをこのように見えるハイパーグラフの一部に変えなさい」ということです。
グラフで言えば、サブグラフを見たときに、エッジの束がこの特定の方法でぶら下がっているものを見たときに、それを別のグラフに書き換える、ということです。なるほど。これが全体の流れです。問題は、「何?つまり、私が言ったように、これは非常に抽象的なものだと考えてください。疑問の一つは、どこで更新を行うのかということです。この巨大なグラフを手に入れたわけですね。
Lex Fridman 1:05:31
Outdatingのきっかけは?例えば、何が?その波及効果は何ですか?そうですか?そうですね、すべてのものは時間的にも離散していると思います。
OK、では質問ですが、なぜアップデートをするのですか?
Stephen Wolfram 1:05:41
そうですね。その答えは、適用される場所でアップデートを行うというルールです。そして、更新を行う順番は定義されていません。つまり、あなたがそれらを行うことができるということです。そのため、これらのアップデートの順序には様々な可能性があります。
さて、重要なのは、もしあなたがこの宇宙の観察者であるイマジンが、何かが更新されたかと言った場合です。あなた自身が更新されるまで、ある意味ではわかりませんよね。そうでしょう?つまり、あなたが敏感に反応できるのは、基本的には、あちらの出来事が自分の中の出来事にどう影響するかという因果関係のネットワークだけなのです。
Lex Fridman 1:06:22
観察という感じではありませんね。それは何か別のものであり、あなたは全体の一部に過ぎないということです。
Stephen Wolfram 1:06:28
はい、あなたはその一部ですが、しかし、持っていることさえも。私は観察者の構造のようなものについて大きな声明を出しているわけではありません。なぜなら、観察者が影響を受けることができるのは、観察者の中の出来事が、宇宙で起こった他の出来事にどのように影響されるかという、この因果関係のネットワークだけだからです。観察者が影響を受けられるのは、この因果関係のネットワークだけです。つまり、これらの書き換えは、気が向いたときにどこでも起こっているのです。
Lex Fridman 1:07:18
因果関係のネットワークがあると思っても、実際にはないと言っていたので、このアイデアは、何が更新されるか、物事の順序が未定義であるようなものになります。それはそうですね。因果関係のあるネットワークというのは、そういう意味です。
Stephen Wolfram 1:07:35
因果関係ネットワークは、更新が起こったことを前提にしています。因果関係があるかどうかは、その出来事が起こらなければ、未来の出来事はまだ起こらないのか?そうです。このようにして、何が何に影響を与えるかというネットワークを構築していくのです。
分かりました。そのネットワークが構築されると、それが宇宙の観測可能な側面のようなものになります。そうなると、宇宙で起きていることの観測可能なネットワークがどれくらい強固なものなのか、という質問ができるようになります。さて、ここからがちょっと面白いところです。
ある種の微視的な書き換えルールでは、書き換えの順番は因果ネットワークには関係ないのです。これは数学的論理の瞬間です。これは、書き換えルールの教会名簿特性や合流特性と同じです。
これは、例えば代数式を単純化するときに、「ああ、これらの項を展開してみよう、これらの部分を因数分解してみよう」と言えるのと同じ理由です。どのような順序で行っても、常に同じ答えを得ることができます。これは、ある種の微視的な書き換えルールを引き起こすのと同じ基本的な現象であり、因果ネットワークが書き換えの微視的な順序に依存しないことを意味しています。
なぜその性質が重要なのか?それは、特殊相対性理論を示唆するからです。この性質が重要なのは、特殊相対性理論によると、異なる参照フレームを見ることができ、ある速度で移動しているかどうか、他方よりもこちらを行っているかどうかによって、空間と時間の概念が異なる可能性があるからです。
しかし、それにもかかわらず、物理学の法則は同じです。特殊相対性原理では、参照フレームに関係なく物理法則は同じであるとされています。さて、このような微視的な書き換え順序の変更は、本質的には参照フレームの変更と同等であることがわかりましたが、少なくともその仕組みの小部分があります。
それは、参照フレームの変更によるものです。だから、ちょっと意外なことに、ある意味、初めてであり、永遠でもあるのです。特殊相対性理論を導出するために、基礎となる微視的な理論が特殊相対性理論を暗示することは可能なのです。因果的不変量は、宇宙に一本の時間の流れがあることを暗示する特性でもありますが、観測者が確定的なことが起こると考える可能性につながるものではないかもしれませんね。
そうでなければ、すべての可能な書き換え順序があり、どれが起こったか誰にもわからないことになります。しかし、この因果的バリアントの特性により、時間の明確な脅威という概念が存在します。
Lex Fridman 1:10:25
それは、そのような時間や空間の概念がシステムから生まれてくるように聞こえます。
Stephen Wolfram 1:10:33
ああ、そうですね、そうではありません。基本的なレベルでは、ハイパーエッジなどで接続されたノードの束があるだけです。
Lex Fridman 1:10:39
時間もなければ空間もない。
Stephen Wolfram 1:10:40
その通り、フィットします。しかし問題は、想像するようなもので、想像してみてください。ハニカムグラフのようなものがあるとします。このグラフは、ミクロのレベルでは、ノードが他のノードに接続されているだけです。しかし、巨視的なレベルでは、それはアニコンのように見え、格子のように見え、2次元のように見え、ある種の多様体のように見えます。
もし、別の方法で接続すれば、すべてのノードを1つずつ接続し、リンクリストのような構造にすれば、それは1次元の空間のように見えると言うでしょう。しかし、微視的なレベルでは、これらはすべてノードを持つネットワークに過ぎず、巨視的なレベルでは、私たちがよく知っている種類の空間のように見えるのです。
ハイパーグラフでも同じことが言えます。では、どうやって3次元の空間が得られるものを見つけたのかと聞かれると、答えは「まだ」です。つまり、このようなものがあるかどうかはわからないのです。
いわば自然に賭けているようなもので、知るすべがありません。この種のシステムには、他にも多くの特性があります。それは、非常に美しく、実際に、非常に示唆的であり、このシステムが正しいと判明した場合には、非常にエレガントになるでしょう。
そして、すべてが構築されていく……空間についてのすべて、時間についてのすべて、物質についてのすべて。すべては、この非常に低いレベルのシステムの特性から出現したものなのです。もしそれが私たちの宇宙の仕組みであれば、とてもクールなことです。
一方で、私が非常に混乱しているのは、仮に成功したとしても、この特定の種類のハイパーグラフ自由記述規則が宇宙を与えると言えるとしたら、そのハイパーグラフ書き換え規則を十分な回数実行すれば、すべてが得られるでしょう。
もし私たちがそこに到達して、これは何なのか、私たちが今持っているこのルールは何なのかを見てみると、それは私たちに全宇宙を与えてくれるものなのか?
それをどうやって考えるかですが、「これのミニマムバージョンが判明しました」「これはちょっとクールなものです」と言えばいいのです。私のような言語設計者にとっては、このモデルの最小バージョンは、実際には1行の言語コードになります。そんなことになるとは思っていませんでした。でもそれは、実際の特定のハイパーグラフを知るためのフレームワークであって、ルールの仕様はどうなっているのか、というような長いものになるかもしれません。
Lex Fridman 1:13:14
それが何の役に立つのでしょうか?宇宙を創造するシンプルさの美しさと優雅さに驚嘆する以外に?それは何かを予測するのに役立ちますか?非簡約性のため、あまり役に立ちません。
Stephen Wolfram 1:13:25
その通りです。その通りです。しかし、私にとって本当に不思議なのは、まだ自分の頭の中で整理できていないのですが、私たちは宇宙の中心に住んでいるわけでもなく、何か特別なことをしているわけでもない、ということに気付き続けていることなのです。
しかし、もし私たちが宇宙のルールを作ったとしたら、それはとてもシンプルなもので、それを書き出すことができます。いわば、利用可能な宇宙の多くは、信じられないほど複雑で、5兆文字もあるかもしれないのに、どうしてシンプルな宇宙ができたのでしょうか?なぜシンプルな宇宙を手に入れることができたのか?私はそのことを理解していません。まだね。
Lex Fridman 1:14:10
もし本当に私たちがそのような単純なルールで、宇宙が この外側に何かがあって、私たちは人々がそう呼ぶシミュレーションのようなものの中にいるということは可能でしょうか?私たちは、別の宇宙で大学院生が研究している計算の一部に過ぎないのでしょうか?
Stephen Wolfram 1:14:31
問題は、私たちは自分の宇宙の外にあるものについてあまり語ることができないということです。なぜなら、定義上、私たちの宇宙とは私たちが存在するものだからです。そうですね。では、私たちの特定の宇宙がどのように機能しているかを知ることで、神学的ともいえる結論を出すことができるのでしょうか?興味深い質問ですね。
この質問は、地球外知的生命体についての質問と関連しています。宇宙のルールはわかっていますが、それが意図的に作られたものかどうかはわかりません。
それは、どこかのランダムな星から受信している信号を見ているのと同じことです。それは一連のパルスです。周期的な一連のパルスですが、これは意図的に行われたのでろうか。その一連のパルスの起源について、何か結論を出すことはできるのか。
Lex Fridman 1:15:21
エレガントだからといって、誰かがそれを作ったとは限らないし、我々が理解できるとも限らないのでは?
Stephen Wolfram 1:15:29
これは、技術的な特徴を特定する質問の究極のバージョンだと思います。
私たちの宇宙は、いわばテクノロジーの一部だったのでしょうか?いったいどうやってそれを知ることができるのでしょうか?
なぜなら、それはつまり、あなたが想像するようなクレイジーなSFのようなもので、ああ、誰かが持っているだろう、そこにはサインがあるだろう、それはつまり、ああいう人が作ったものだ、と言うことができるでしょう。
しかし、それを理解する方法はありません。なぜなら、宇宙は、単純に、宇宙のルールを見つけたとしても、私たちは、そのルールが宇宙の行動を表していると言っているだけだからです。古典力学の法則や微分方程式などが機械システムの動作を表しているのと同じ意味で、その法則が宇宙の動作を表していると言っているだけなのです。
Lex Fridman 1:16:39
では、そのギャップとは?あなたの感覚では、長続きしますか?魅力的で、もしかしたら少しSF的な質問ですが。宇宙を作る基本的なルールを理解することと、システムをエンジニアリングすること、つまりあなたが話したようなシミュレーションを実際に自分で作ることとの間には、どのようなギャップがあるのでしょうか?そんなところでしょうか。
あなたは、ナノエンジニアリングのようなアイデアについて話しましたが、これは実際に物理的な空間で計算のアイデアを作り出すという、エキサイティングなものですよね?宇宙を創造することは、工学的にどのくらい難しいことなのでしょうか?ルールがわかれば、創造者の役割を果たすことができるのでしょうか?
Stephen Wolfram 1:17:12
宇宙が作動している基盤は、私たちがアクセスできる基盤ではないと思います。つまり、私たちが持っている唯一の基盤は、宇宙が作動しているのと同じ基盤なのです。
つまり、宇宙が書き換えられているハイパーグラフの束であるならば、私たちは書き換えられている同じハイパーグラフに自分自身をくっつけることができるのです。私たちにはできません。もしあなたが、コードはきれいか?効率的なアルゴリズムなど、エレガントで美しいコードを書くことができるかどうか、ということです。
Lex Fridman 1:17:44
これは面白い質問ですね。これは、システムの中にどれだけの計算の非簡約性があるかという問題です。しかし、基本的に自分自身の中に自分自身のコピーを作り出す美しいセルラーオートマトンを見たことがあります。そうですね。これは、創造することが可能かどうかという問題で、例えば、基質を理解する必要があるのか、それともできるのかということです。
Stephen Wolfram 1:18:04
ああ、そうですね。つまり、私が考える未来のちょっとしたSF的な考えのひとつに、「物理学の基礎理論を見つけることは重要だと思いますか」という典型的な人たちを対象にしたものがあります。少なくとも私は非公式にこの世論調査を行ったことがありますが、興味深いことに、実際には、かなりの割合の人々が「ああ、それはとても興味深いことだ」と答えています。
Lex Fridman 1:18:27
それは意外にも多くなってきていると思います。つまり、多くの人が物理学に興味を持ち、理解せずに、ごく少数の科学者が現実の本質を理解しようと奮闘しているのを見ているようなものです。
Stephen Wolfram 1:18:46
でしょう?つまり、それはある程度正しいと思います。実際、私が始めようとしているこのプロジェクトでは、物理学の基礎理論を見つけようとしていますが、これは非常に公共性の高いプロジェクトとして行うつもりです。つまり、ライブストリーミングで配信する予定なんです。
そして何が起こるかわからない。それはとても楽しいことです。つまり、このプロジェクトの世界へのインターフェイスだと思うんです。このプロジェクトの特徴のひとつは、基本的にありのままのテクノロジー・プロジェクトとは異なり、これは単純に失敗するかもしれないプロジェクトだということです。
なぜなら、私たちがたまたま住んでいる物理的な宇宙とはまったく関係のない、あらゆる種類のエレガントな数学を生成するかもしれないからです。さて、ここでは物理学の基礎理論を見つけるための探求の話をしています。
最初のポイントは、物理学の基礎理論を見つけるのは難しいと分かったことです。1600年代に数学を科学に応用した初期の頃、人々は「ああ、あと100年もすれば、宇宙の仕組みについてすべてがわかるだろう」と考えていましたが、実際にはそれよりも難しいことがわかりました。
というのも、宇宙を研究するために、より小さなレベルに到達するたびに、数学はより複雑になり、すべてがより難しくなっているように思えたからです。私が子供の頃は、基本的に素粒子物理学をやっていました。素粒子物理学をやっていたとき、物理学の基本的な基礎理論を見つけることは、とんでもないことで、絶対にできないと思っていました。しかし、場の量子論や一般相対性理論などを行うために構築したこれらの枠組みの中で活動することはできます。それはいいことだと思います。そして、多くのことを解明することができます。
Lex Fridman 1:20:26
その時にも、何か裏があると感じていたのですか?
Stephen Wolfram 1:20:29
もちろん、予想外でしたね。というのも、文明の世界では、古代人がすべてを解明していると考えられていた時代が長く続いていたからです。私たちは何も新しいことを理解できないだろう」と考えていたのです。いわば、物理学をやっている最中に感じたことですが、量子場の理論が我々のやっていることの基礎になっていると。
その下に何かがあるんだろうけど、それを解明することはできないだろう」というものでした。しかし、その後、私は計算世界の単純なプログラム、例えばセル・オートマトンなどの研究を始めました。すると、それまでの直感とはまったく違うことをやっていることがわかったのです。
その後、驚くほど複雑なことをする小さな小さなプログラムを目の当たりにして、物理学に対してもう少し野心を持つようになり、物理学でもこれができるかもしれないと思うようになりました。これが、数年前に私が始めたきっかけです。一般相対性理論における場の量子論など、これらすべての枠組みの下にあるものを実際に見つけられないだろうか、という考えです。
人々はあまり気付いていないかもしれませんが、私たちが物理学に使っている枠組みは、基本的にこの2つ、場の量子論、一般相対性理論における小さなものの理論、重力と大きなものの理論、これら2つの基本理論です。この2つの基本理論は100年前のものです。
一般相対性理論は1915年、場の量子論は1920年代ですから、基本的には100年前の理論です。しかし興味深いのは、それ以前の200年の間にも何度か基礎が変わっていたにもかかわらず、その期間中に基礎が変わっていないことです。
私が考えているようなことは、「計算の世界」における「計算」について考えることから得られたものですが、これは別の基礎なのです。
異なる基礎であり、間違っているかもしれませんが、少なくとも私たちには可能性があります。これは、私にとっては、自分自身のための個人的な計算なのです。もし、物理学の基礎理論を発見することがわかったとしても、それはいわば低空飛行の果実のようなもので、やろうと思わなかったとしたら残念なことです。
と言われて、誰もやらないまま200年経ってしまったとしたら、とても残念です。実際のところ、ぶら下がっている果実がどれほど低いかはわかりませんがね。もしかしたら、このプロジェクトを行うには間違った世紀なのかもしれません。つまり、私にとっての訓話は、私がテクノロジーの分野でやろうとしたことについて、もっと前から人々が考えていたことだと思います。
私の好きな例は、おそらくライプニッツです。ライプニッツは、1600年代後半に世界の知識を本質的にカプセル化して計算で表現しようと考え、それに向けて多くのことを行いました。しかし、彼は300年早かったのです。これは、人生設計の観点からすると、とても重要なことなのです。いわば、「自分の世紀にできないことは避けよう」ということです。
Lex Fridman 1:23:51
タイミング、タイミングがすべてです。
もし私たちが、場の量子論や一般相対性理論を生み出すことができる基本的なルールを理解したとしたらどう思いますか?それは、そのレベルのトラックで統一するのに役立つと思いますか?
Stephen Wolfram 1:24:09
完全に分かるようになります。すべてがどのように組み合わさっているかがわかるでしょう。はい、間違いありません。つまり、私がすでにやったことでさえ、すでにそうなのです。非常にエレガントで、実際に、物事がどのように組み合わされていくのかがわかります。それが正しいかどうか?まだわかりません。非常に示唆に富んでいます。もしそうでなければ、そうですね。もしそうでなければ、宇宙の設計者は、いわば恥ずかしいと感じるべきだと思います。
Lex Fridman 1:24:36
あなたの直観では。
宇宙をデザインするという点では、神はサイコロを振っているのでしょうか?このものにはランダム性があるのでしょうか?それとも、決定論的なのでしょうか?
Stephen Wolfram 1:24:46
書き換えを伴うようなものを扱っていると、ちょっと複雑な質問になってしまうんですよね。つまり、多くのシステムにおけるランダム性は、擬似的なランダム性とランダム性を区別するのが難しいのです。
この特定のケースでは、量子力学における測定についての現在の考えは、非常に奇妙で非常に抽象的なものです。非常に技術的なことを話さない限り、まだ説明できないと思いますが、もしそれが正しいとすれば、それは一種の奇妙なもので、決定論とランダム性の間を、これまでにない奇妙な方法で切り取っているからです。
ですから、科学の世界で出てくる多くの疑問のように、「これか?それともあれか?」本当の答えは、そのどちらでもなく、それらのカテゴリーとは異なる、直交する何かだということがわかりました。これが現在の、つまり今週のアイデアですが、どのように機能するでしょうか。
しかし、それがどのように展開するかは、これからのお楽しみです。つまり、物理学のような分野では、基礎理論の探求などの問題があります。なぜなら、基本的に物理学のように古い分野では、私たちは物理学者の第4世代か、第5世代かわかりませんが、そのような世代になっているからです。
私もいわばその一人でした。私にとって、基礎はいわばピラミッドのようなもので、そういうものだったのです。そして、常にそのような状態でした。古い分野では、基礎に戻って書き直すことは難しいのですが、若い分野では、その分野を発明した第一世代の人たちを相手にしているので、はるかに簡単です。
また、科学の世界で起こることの性質として、方法論的な進歩が起こると、典型的なパターンになります。その後、5年、10年、もしかしたらもう少し長い期間があり、その方法論の進歩によって多くのことが可能になります。それが望遠鏡であろうと、数学的な方法であろうと何であろうと、何かが起こり、道具が作られ、そして多くのことができるようになります。
そして、たくさんの低空飛行の果実を収穫することができます。それにはある程度の時間がかかります。その後、低空飛行の果実をすべて摘み取った後は、次の何十年、何百年、あるいはそれ以上の期間、何かができる次のレベルに到達するために、大変な努力をしなければなりません。巡航モードとまでは言いませんが、本当に大変な仕事ですが、非常に漸進的な進歩のための非常に大変な仕事です。
Lex Fridman 1:27:47
あなたのキャリアや、あなたが引き受けたいくつかの仕事を見ていると、あなたは苦しい仕事を恐れていないように感じます。特に工学的な面では非常に興味深いですね。
ちょっとした余談ですが,カリフォルニア工科大学ではリチャードファインマンの素晴らしい物理学に触れることができましたか?
Stephen Wolfram 1:28:10
実際、かなり一緒に仕事をしていました。実は、私がCaltechにいた時も、Caltechを辞めた後も、私たちは共にthinking machines Corporationという会社のコンサルタントをしていましたが、この会社はここからすぐ近くにあったのですが、実は最終的には不運な会社でした。
最終的には不運な会社になってしまいましたが、私はよく、「この会社は5番デッキで考えている戦略ではうまくいかない」と言っていました。いずれにしても、彼はそういうことには興味がありませんでした。そして彼は、私が会社経営のようなことに興味を持つのは、いわば気晴らしだと考えていたようです。私にとってそれは、実際に物事を成し遂げ、物事を理解し、物事を実現するためのより効果的な機械を持つためのメカニズムなのです。
Lex Fridman 1:28:59
彼はそれを考えたのでしょうか?基本的には、あなたが会社で使っていたものを、あなたがそのように考えていたかどうかはわかりません。しかし、あなたは大学での研究を強化するためのツールを作っているのです。
彼はその点を理解していたと思いますか?
Stephen Wolfram 1:29:18
でも、彼は私の最初の会社で、もっと数学的な計算に関わっていたんですよ。彼は、私たちが何をすべきかという技術的な側面について、たくさんのアドバイスをしてくれました。
Lex Fridman 1:29:39
思い出や考えていることを教えてください。そうですね。
Stephen Wolfram 1:29:41
彼は、数学で難しいことの1つである積分などを行うビジネスにおいて、あらゆる種類の幸運を手に入れました。そこで彼は、積分などを行う独自の精巧な方法を持っていました。また、数学がどのように機能するかを直感的に理解するための独自の考え方も持っていました。
彼の優れたアイデアは、そのような直観的な方法を用いて、コンピュータにその直観的な方法に従わせるというものでした。ほとんどの場合、私たちが積分などを行うときには、このような奇妙な産業機械を作って、すべての積分をムルギー関数の積まで回転させて、非常に精巧なものを生成することがわかりました。
そして実際、大きな問題はその結果を人間が理解できるようなものに変えることです。積分をしているわけではないのです。お恥ずかしい話ですが、ファインマンは50年代に研究した素粒子物理学の計算方法を山のようにくれたことがあります。
彼は「そうだね、僕よりも君の方が慣れているからね」と言っていました。私はそれを見て、返すつもりでした。そして、私は今、ファイルを始めました。でも、それは人間の命が有限であるがゆえに起こることです。もしかしたら、あなたがあと20年生きていたら、私はそれを返すのを忘れないようにしなければならないかもしれませんね。しかし、これは彼が体系化しようとしたものだと思います。素粒子物理学などを研ぎ澄ます積分のやり方は、実際にやってみると、そのやり方とはまったく違うことがわかったのです。
Lex Fridman 1:31:09
その違いについてはどう思われますか?難しい概念を理解するための直感的なフレームワークを作ることに、フィンマンは非常に優れていましたか。
Stephen Wolfram 1:31:23
なぜなら、彼の面白いところは、彼が本当に、本当に、本当に得意だったのは、計算することだったからです。でも、彼はそれが簡単だと思っていました。なぜなら、彼はそれが本当に得意だったからです。だから、彼は複雑な計算をして、例えば場の量子論を計算して、結果を出しても、複雑な計算のことは誰にも言わない。
彼は、本当に素晴らしいのは、すべての仕組みについてシンプルな直感を持つことだと考えていました。だから、彼は最後にそれを発明した。そして、計算をしてその仕組みを知っていたからこそ、より簡単に、答えがわかっていればより簡単に、優れた直感を持つことができたのだと思います。
そして、その計算結果を誰にも教えないようにしたのです。悪意があったわけではありません。ただ、それが簡単だと思っただけなのです。そう。その結果、人々が完全に困惑するような分野にまで発展してしまったのです。そして、人々は彼の直観に従ったのです。
でも、なぜそれがうまくいったのかは誰にもわかりませんでした。実際には、うまくいった理由は、彼がすべての計算をして、うまくいくことがわかっていたからです。私がお金を出して、量子コンピューターの研究を少ししたのは、80-81年のことでした。
今になって考えてみると、私は彼と一緒に仕事をしていた頃の彼と同じくらいの年齢になっていて、いわば私と同じ年齢の人たちが1/3になっているんですね。彼は、私が彼の年齢の1/3であることをいつも不満に思っていましたが、しかし、彼は手で計算して、黒板などを使って答えを出していました。
私が「これはわからない、私はコンピューターで計算する」と言うと、彼は「わかるだろう。彼は、「これはわからない」と言うでしょう。だから、何が起こっているのかについては大きな議論があるのですが、いつも何かしらの答えが返ってくるのです。
実際、量子コンピュータについて私たちが気づいたことの多くは、特に測定プロセスに関係する問題であり、それは現在でも問題となっていると思います。私はそれが面白いと思っています。科学というのは不思議なもので、技術にも驚くべきことが起こるのです。
驚くべき歴史の繰り返しが、結局は起こってしまうのです。最終的には、物事は本当に釘付けになります。しかし、それには時間がかかります。
そして、何十年も経ってから戻ってくることも多いのです。例えば、ここからすぐ近くで実際に起こった話をしましょう。私たちが機械を考えていた頃、私はあるセル・オートマトンに30年以上取り組んでいました。愚かな物理的なことですが、あの会社が作っていたコネクションマシンと呼ばれる大きな並列コンピュータを使って、私はルール30の巨大なプリントアウトを作成しました。
つまり、高解像度の大判プリンタですね。これで、非常に小さな細胞をたくさん印刷することができました。そのパターンのいくつかの特徴をどうするかという問題がありました。床の上で測光器を使っていろいろなものを測ってみるという、まさに物理的な作業でした。
それで、Fineemanは私を連れて行ってくれたんです。私たちは少しの間そのようなことをしていましたが、彼は私を脇に連れて行き、「私はこれを知りたいんだ」と言いました。一つは、このルール30というものが、我々が大きなプリントアウトなどをしているほど複雑な挙動を生み出すということを、どうやって知ったのかということです。
私は、ただ可能性のあるルールをすべて列挙しただけなのに、それがどうなったかを観察してみたら、ずいぶんと気分が良くなったんです。あなたには、彼にはない直感があると思っていました。それはなぜですか?いやいや、直感ではなく、ただの実験科学です。
だから

Lex Fridman 1:35:26
まさにあなたが示したのは、非簡約性概念について直感を持つことはできないということなのです。つまり、私たちを動かす必要があるということです。そう、その通りです。私たち人間にとって、特に優秀な物理学者にとって、全体がどのように動いているかについて、圧縮されたきれいな直感を持つことはできないと言うのは、とても難しいことです。
Stephen Wolfram 1:35:52
はい,作品。はい。いいえ、彼はそうでした。つまり、彼は計算に関するその点を理解するギリギリのところにいたのだと思います。そして、彼はいつも計算の面白さに気づいていたと思います。そして、それが彼のちょっとした突っ込みどころになっていたのではないでしょうか。
つまり、直感的には、「すべてのケースを列挙して、何か面白いことをするものを見つければいいんだ」と言っても、それを発見するのは難しいということですよね。とても簡単そうですよね。でも、最初に見たときには見落としていたんですよ。だから、そのケースは無視しようと思っていました。
Lex Fridman 1:36:29
では、どのようにして、どうやって心を開いたのですか?なぜなら、あなたは本質的に同じ人間だからです。
あなたの戦いは、同じ種類の物理学的なタイプの考え方のようなものですか?どのようにして、自分がルールを見るのに十分なオープンマインドを持っていたのか?そして、複雑さを明らかにしたのですか?
Stephen Wolfram 1:36:44
それは興味深い質問ですね。私自身もそのことを不思議に思っていました。というのも、こういったことを経験しながら生きているようなものだからです。そして、歴史的なストーリーとは何だったのか、ということになりますが、後になって気づく歴史的なストーリーは、いわば自分が生き抜いてきたものではなかったということもあります。
私は物理学を専攻していましたが、それは還元物理学のようなもので、宇宙を投げて、その中で何が起こっているのかを考えろというものでした。そして、コンピュータ・ツールを作り始めました。例えば、私は最初のコンピュータ言語を作り始めました。
コンピュータ言語は物理学のようなものではありません。人々がやりたいと思っている計算をすべて取り上げ、それらがすべて成り立つようなプリミティブを掘り下げて見つけなければなりません。しかし、それとは全く違うことをするのです。「よし、これがプリミティブだ」と言うだけですから。
うまくいけば人の役に立つかもしれないから、そこから積み上げていこう。つまり、ある意味では、本質的に人工的な宇宙を構築しているのです。この言語を作り、これらのプリミティブを手に入れ、自分が作りたいと思うものを何でも作っていくのです。
これは私にとって興味深いことでした。宇宙を宇宙のままに投げ出すような科学をしていたのに、「どんな宇宙を作ってもいいんだよ」と言われたのですから。コンピュータ言語を作るということは、いわば自分自身の宇宙を作ることですから、その経験が私に可能性に対する考え方を変えさせたのだと思います。自然科学のように「宇宙が実際にどうなっているかに制約されよう」と考えるのではなく、このような人工的な宇宙で何ができるのかを探ってみよう、というわけです。
Lex Fridman 1:38:25
基本的にプログラムできることで、自分の心とペンだけに制限されていたのが、今では基本的に別の脳を構築し、それを使って宇宙を探索することができます。
Stephen Wolfram 1:38:41
望遠鏡というか、道具というか、いろいろなものを見ることができますよね。
しかし
Lex Fridman 1:38:46
コンピュータと望遠鏡の間には何か根本的な違いがあります。つまり、概念をロマンチックにしているだけで、もっと一般的なものなのです。
Stephen Wolfram 1:38:57
より一般的でしょうか?この点については、「ああ、こんな時にこんなことが発見されそうだった」と言われますが、実際に物事を理解するためのパラダイムを構築することと、何が起こっているかを見極めるためにオープンになることとの間の距離は、とても遠いのです。
これは本当に難しいことです。私の人生は幸運にも、計算言語の構築に多くの時間を費やしてきました。これは、ある意味では、別の抽象レベルを作り出し、さまざまな種類の構造に対してオープンでなければならないという活動です。しかし、私はいつも、つまり、何度も見てきたことで、いかに明白なことを見逃すのが簡単であるかという事実を十分に認識していて、少なくとも明白なことを見逃さないようにするための努力をしています。
成功しないかもしれませんが
Lex Fridman 1:39:57
数学や科学の歴史における自我の役割は何だと思いますか?もっと言えば、本のタイトルのように、新しいタイプの大きさで、あなたは膨大な量を達成した。実際、誰かが「ニュートンにはエゴがなかった」と言っていました。そして、それを調べて、大きな1年を過ごしました。そうですね、外野から見ると、あなたにも少しエゴがあると言う人もいます。そのようにお考えですか?エゴは邪魔になりますか?エゴが邪魔をするのか、それとも力を与えるのか。
その両方でしょうか?
Stephen Wolfram 1:40:32
それは複雑で必要なことでしょう。つまり、私は、人生の半分以上をハイテク企業のCEOとして過ごしてきました。そうですね。それはつまり、自分のエゴが遠い存在ではないということだと思うんです。エゴは、いわば毎日のように遭遇するものです。
なぜならば、リーダーシップや、組織をどのように発展させていくかなど、さまざまなことと結びついているからです。例えば、私が学者だったら、自我をチェックして、それをどこかの棚に置いて、その特徴を無視することができたかもしれませんが、しかし、あなたはそれを思い出すのです。
Lex Fridman 1:41:11
会社を経営していると、よく思い出しますよね。確かに、そうですね。
Stephen Wolfram 1:41:15
つまり、それはそういうことなのです。リーダーシップの話です。そして、リーダーシップは自我と密接に結びついています。さて、エゴとは何でしょう?つまり、今の時点では、誰かが私に何かを教えてくれたとしても、それが理解できないという結論ではなく、私の結論は、言われたことに何か問題があるということです。そして、これは実際にFineemanが以前持っていたもので、彼は決して専門家を信じていたわけではなく、実際には私が専門家を信じるよりもずっと専門家を信じていたのです。だから、えーと。
Lex Fridman 1:41:57
ワオ。自我の基本的に強力な特性として、「自分が間違っているのではなく、世界が間違っている」と言い、自分が本当に考え抜いたことと一致しない事実に直面したときに、それを教えてくれるというものですね。エゴのマイナス面とプラス面の両方ですね。
エゴの負の部分が邪魔になったり、周りの目を気にしたりすることはありますか?
Stephen Wolfram 1:42:31
私たちが犯した失敗は、「自分は正しい」と確信していたにもかかわらず そして、結果的にはそうではなかったのです。つまり、そういうことなんです。しかし、重要なのは、人は何かをしようとするという考え方です。例えば、1つの質問は、人々が何かをしようと懸命に努力したときに、自分もやってみようかなと思うかどうかということです。
そうですね。私は幸運なことに、若い頃から科学などである程度の成功を収めていました。そのおかげで、他の方法では得られなかったであろう、ある種の知的な自信を得ることができました。ある意味では、ですね。つまり、私は幸運にも、素粒子物理学の分野で仕事をしていました。というのも、急速に拡大している分野で、たまたま低空飛行の果実を摘んでいれば、生き残りそうなものを発見するのは簡単だからです。
Lex Fridman 1:43:11
その理由として、私は新しい種類の科学の背後にあるエゴを、すぐに理解することができました。そのようなエゴを許さなければ、そのような本を書くことはないでしょう。私が思うに、そのような自我を持ち、それに乗って、自分がどこに連れて行かれるのかを見なければならないのです。そうすることで、優れた作品を生み出すことができるのです。
Stephen Wolfram 1:44:03
あの本のもう一つのポイントは、些細なことではない問題だったと思います。それなりに大きなアイデアだと思われるたくさんのアイデアを、どうやって取り上げるかということです。そして、その範囲はかなり大きいのです。そして、それまでのものとは非常に異なっています。
そこで問題になるのが、その内容をどうやって人々に説明するかということです。そこで私は、「セルラー・オートマトン」というものがあって、これをやったり、これをやったりするんだよ」と言った経験があります。そうすると、人々は「ああ、これと同じようなものに違いない。そうに違いない。」しかし、そうではありません。何か違うんです。
Lex Fridman 1:44:42
私ができたのは、あなたができたことを本当にうれしく思います。学術的には、小さな論文をあちこちで発表し続けることだけでした。そうすると、このような抵抗を受け続けることになりますよね。「これが私の全作品です」というものを出すのです。
Stephen Wolfram 1:45:00
いいえ、私が計算したのは、基本的には、小さな断片を導入することができる、ということでした。でも、私は決めたんです。利害関係者には1つの人生があり、彼らを導くためには1つの人生がある。私は、一番良い方法は、いわば知的内容を最も尊重することであり、できる限りの力でそれを発信することだと思いました。
というのも、エゴの話は興味深いものがありますよね。例えば、私は自分の名前を冠した会社を経営していますよね。私は、自分の名前が入った会社を経営している人たちのためのクラブを始めようと思いました。面白いグループですね。私たちはエゴの塊ではありませんし、いわばそういうものでもありません。
基本的には、自分のやっていることに責任を持つということです。そして、ある意味では、自分自身を危険にさらすようなことをしているのです。私の会社は、ある意味では私の名前がついているだけのものです。しかし、会社は私よりも大きな存在で、私はある意味、会社のマスコットのようなものです。つまり、私はたまたまその会社のかなりの、つまり強力なリーダーでもあるのです。
でも、でも、基本的には
Lex Fridman 1:46:37
スティーブ・ジョブズのように、同じ自分の名前への深い、切り離せないような投資を示しています。彼の名前はAppleのものではありませんでしたが、彼はAppleでした。イーロン・マスクの名前はテスラの名前ではありませんが、彼はテスラなのです。
つまり、会社が成功しても失敗しても、彼は感情的にそのことで苦しむという意味を持っているのです。その事実を認識しているということです。また、ブランド名としても優れています。それでうまくいったのです。スティーブが悪い契約をしてしまったように。
そうだね。それを名字で補ったわけですね。そうですね。2002年、あなたは新しいタイプの科学を発表しましたが、個人的にはセルラー・トムラや計算への愛を評価しています。他の多くの人たちも同様だと思います。
この1200ページの本に示されているビジョン、希望、主要なアイデアを簡単に説明していただけますか?
Stephen Wolfram 1:47:46
もちろんです。本の中で述べるには1200ページも必要でしたが。本当のアイデアを知るには、歴史の流れを見て、科学の発展に何が起こったのかを知るのがいいでしょう。つまり、世界で起こっていることを記述するために、数式を使おう、というものです。このように、自然界を記述するのに数式を使うことが300年にわたって行われてきましたが、これは非常にうまくいきました。
しかし、私はこの概念をどのように一般化できるかに興味を持ちました。形式的な理論があり、明確なルールがあるが、そのルールにはどのような構造があるのか。そこで私が興味を持ったのは、純粋に数学的なルールを超えて一般化しようということでした。
現在、プログラミングやコンピューティングなどの概念がありますが、世界を記述する方法として数学に存在する規則の一般化として、プログラムに具現化できる規則の種類を利用しようと考えました。私が好きなのは、セル・オートマトンと呼ばれる単純な規則のバージョンです。典型的なケースですね。
Lex Fridman 1:49:10
セル・オートマタとは何でしょうか?
Stephen Wolfram 1:49:13
そうですね。セル・オートマトンの典型的な例としては、細胞の配列が挙げられます。単なるバラバラのセルが並んでいるだけのものです。各セルは黒か白のどちらかです。そして、ページを進む線で表現できる一連のステップでは、上や左右のセルの色に依存するルールに従って、各セルの色を更新します。とてもシンプルですね。
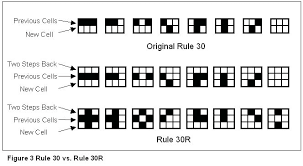
例えば、あるセルとその右隣のセルの色が同じではない場合です。また、左隣のセルが黒だったりする場合は、次のステップで黒にし、そうでない場合は白にします。典型的なルールで、正確に言ったかどうか自信がありません。今言ったようなルールは、一番上の1つの空白のセルから始めた場合、非常に複雑なパターンを作るという特徴があります。
あるルールでは、非常に単純なパターンが得られます。あるルールでは、ルールが単純で、ある種の単純な種から始めれば、非常に単純なパターンが得られます。しかし、他のルール。これが大きな驚きでした。実際に単純なコンピュータ実験を行って何が起こるかを調べてみると、非常に複雑な行動パターンが生成されるのです。
例えば、このルール30は、一番上の1つの黒いセルから始めて、非常にランダムなパターンを作るという特徴があります。中央の列のセルを見ると、一連の値が表示されています。黒、白、黒、黒、何であれ、その順序は実用上はランダムに見えます。
つまり、数学のようなものです。円周率3.1415926の桁を計算しますが、一度計算されたその桁は、円周率を計算するためのスキーム、つまり、円の円周の直径の比であり、非常によく定義されています。しかし、実際に数字を生成してみると、実用的には完全にランダムなものに見えます。
rule30もそうです。円周率の数字を生成するルールよりも非常にシンプルで、計算的に明らかなルールであるにもかかわらず、シンプルなルールであっても、膨大な数の数字を生成しています。それでも、非常に複雑な動作を生み出しているのです。
Lex Fridman 1:51:34
そうですね。あなたはおそらく、あまりにも長い間それを言ったり見たりしてきたので、その魔法を忘れてしまったのではないでしょうか。あるいは、その魔法をまだ感じていないかもしれません。でも、もしあなたが一度も見たことがないとしたら、それは本質的に一次元のものなのでしょうか?
もう一つのドミノですよね?もし、隣の細胞にしか反応しない細胞があるとしたら、何が見えるでしょうか?だろ?私の最初のお客さんのように、最初にあなたの本を開いたときにも、新しい種類の科学、ですよね? マイナーなものは、つまり、とてもシンプルなものを見ることになるでしょう。
あなたが言ったような複雑さを実現するのは、魔法のような経験だと思いますよ。ああ、私の好きなルール?そうですね。複雑さ、膨大な複雑さ、任意の複雑さを得ることができます。そうですね。真ん中の列にランダム性があると言っても、それはクールな言い方のひとつに過ぎません。
信じられないほどの複雑さがあります。これは要点に過ぎません。つまり、これは魔法のようなアイデアなのですが、それを解釈し始めると、非簡約性の議論なども含めて、ただ、この2つにまつわる深遠な哲学的な概念があると思います。私にとっては、世界をどのように見ているかという点で、変化があったと思います。
でも、もし私が無人島にいて、サイケデリックか何かの影響を受けたとしたら、と考えることがあるんです。でも、もし1冊の本を持っていくとしたら、それは科学の世界だと思うんですよ。なぜかというと。少なくとも、それはとても深い概念なのです。
Stephen Wolfram 1:53:32
私はそのように思います。つまり、これは非常に直感的な発見だったのです。つまり、計算の望遠鏡を外に向けてみると、突然、今まで知らなかったことが見えてくる、というようなことです。すると突然、よくわからないが、過去には木星の月か何かを見たことがある。
しかし、突然、思いがけないものが見えてくるのです。私にとってもルール30は予想外でした。そして、個人的なレベルでの大きな挑戦は、それを無視しないことでした。つまり、人々は、言い換えれば、「バグ」と言ってもいいかもしれません。
Lex Fridman 1:54:05
何と言うでしょうか?ええ、まあ、そうですね、つまり、私、私たちは何を見ているのでしょうか、ところで。
Stephen Wolfram 1:54:09
ここでは、ルール30のパターンを生成してみました。これがルール30のルールです。例えば、中央に黒いセルがあり、左に黒いセル、右に白いセルがある場合、次のステップのセルは白になる、と書かれています。例えば、中央に黒、左に黒、右に白のセルがあれば、次のステップのセルは白になります。
これが初期状態、つまり初期のもので、そこからスタートします。そして、ページを進んでいきます。そして、すべてのステップで、このルールを適用して、得られる新しい値を見つけるのです。こんなに単純なルールなら、この単純さの痕跡を得ることができるはずだと思うかもしれません。
さて、400ステップを実行してみましょう。するとどうなるかというと、スクリーン上では少しエイリアスがかかっていますが、左に少しだけ規則性があるのがわかります。しかし、ここには非常に複雑でランダムに見えるものがたくさんあります。少なくとも私の直感では、このようなことが可能だということに大きな衝撃を受けました。
Lex Fridman 1:55:15
すぐに頭の中で、何かパターンがあるのではないかと考え始めます。何か繰り返しのパターンがあるのではないか?ええ、あるはずです。
Stephen Wolfram 1:55:20
そう、心ですね。使ったわけです。確かに、最初はそう思いましたね。そして、まあ、これはちょっと面白いな、と思ったんです。でも、長くやっていれば、何かが解決してシンプルなものになると思うんです。そこで私は、数学や統計学、暗号学などを駆使して、あらゆる種類の分析を行い、解読を試みました。
しかし、一度も成功しませんでした。そして、しばらく成功しないうちに、「ここには本当の現象があるのかもしれない」と思うようになりました。私が成功しない理由はそこにあるのではないか。つまり、私にとって動機となったのは、自然界を見て、自然界に存在する複雑さを目の当たりにしたことでした。
問題は、それがどこから来るのかということです。自然界にはどのような秘密があって、人間が工学的にものを作るときには通常作らないような複雑さを作り出すことができるのか、ということです。非常にシンプルなものから、これほど複雑なものを作っている。もしかしたら、根本的なルールはそれほど複雑でなくても、本当に複雑なものを作ることができる、自然が持っている秘密のようなものが見えてきたのではないか、という衝撃がありました。
Lex Fridman 1:56:30
どのように感じましたか?もし新しいりんごを見たとして、散歩をしていて、何か、深く心に響くものがありましたか?それとも徐々に変化していくものなのでしょうか?多くの出血するような真実、あらゆる種類の科学的発見の真実は、それほど緩やかなものではないのではないでしょうか。
Stephen Wolfram 1:56:49
私は、たまたまサンテリアの伝記のようなものに興味を持っていました。そして、人々がどのようにしてこのようなことを理解するようになったのかを追跡しようとしました。そして、そこにはいつも長い準備のようなものがあります。つまり、何かを見ることができるような心構えが必要なのです。
つまり、ルール30「1984年6月1日頃の起床」の場合、ある意味では馬鹿げた話でしたが、ついに高解像度のレーザープリンターを手に入れたのです。それで、セル・オートマトンの写真をたくさん作ってみようと思ったんです。
そして、この写真を作って、ヨーロッパへ向かう飛行機の中に置いておきました。そうすると、本当にこれを理解しようとしなければならないような気がしてきます。これは本当に、何が起こっているのか理解できません。それは、何が起こっているのかを少しずつ理解しようとしているようなものでした。
いわば、気が滅入るほど不確かなものでした。例えば、計算等価性の原理のような多くのアイデアは、「まあ、これはあり得ることだ」と思っていました。それが正しいかどうかはわかりませんでしたが、今でもそれが正しいことは確かです。しかし、このようなことが徐々に、自分が考えていたよりも重要なことのように思えてくるのです。
つまり、単純なプログラムの計算世界を研究するというアイデアは、本当に重要なアイデアであることを理解するのに、おそらく10年から10年半かかりました。
もし、計算世界の中に全宇宙が潜んでいることが分かったら、それは良いことだと思います。それは、このアイデア全体にとって、良い評価となるでしょう。しかし、私が思うに、不思議なのは、物事のモデルを作るための別の原料を見つけるというこの問題全体において、歴史の弧の中で興味深いのは、300年の間、数学的方程式のアプローチのようなものだったということです。
それが勝者であり、何かのために本当に良いモデルを手に入れたいと思ったら、それを使うことになるのです。驚くべきことに、ここ10年ほどの間に、数式ではなく、プログラムを使って何かのモデルを作るための原材料のようなものに移行してきていると思います。
これはとても素晴らしいことです。いわば、このパラダイムシフトの中で生きてきた人間としては、異様な感じがします。科学の歴史の中で、一瞬にしてパラダイムシフトが起こったとみなされるのは、間違いなく奇妙なことだと思います。しかし、それが実際の生活の中で展開されるとき、いわば瞬間的なものではないことは確かですよね。
なぜなら、そのようなアイデアが様々な分野に採用される際の力学においては、その分野が若ければ若いほど、一般的に早く採用されるからです。なぜなら、この分野を研究してきた第5世代の人たちに縛られることがないからです。そして、それは今のままであり、決して変わることはありません。
そのプロセスを見ていると、とても興味深いですね。つまり、私は幸運な人間だと思います。もし私がそうであれば、自分のすることに対する世間の反応に対して、ある種の厚かましさを感じてしまうでしょう。でも、これは間違いなく、「新しいタイプの科学」というような本を書こうものなら、古いタイプの科学に対しては鉄砲玉が出てくるようなものなんです。
科学の分野でパラダイムシフトが起きようとしているとき、初期の導入時の否定的な反応の強さは、長期的に良い結果をもたらす素晴らしいポジティブな指標であるという事実を、私は十分に認識していました。言い換えれば、人々が関心を示さない場合、それはあまり良い兆候ではありません。人々が「ああ、これは素晴らしい」と思うなら、それはあまり良い兆候ではありません。それは、あなたが何も面白いことを発見していないということです。
Lex Fridman 2:01:00
最近、3つの重要な問題を解決した人に与えられるルール30賞を発表しましたが、これまでに発見したルール30の魅力的な特性は何ですか?rule 30や他のセル・オートマトンが明らかにした興味深い特性について、お話いただけますか?また、今回発表された3つの問題のように、まだどのような問題があるのでしょうか。
Stephen Wolfram 2:01:21
そうですね。そうですね。つまり、セル・オートマトンの最も興味深い点は、それを解明するのが難しいということです。ある意味では、他の技術でセル・オートマトンを解明しようとするたびに、「セル・オートマトンを解読できるのか」ということになります。
その答えは、「クラックできない」ということなんです。還元できない計算をしているという特徴があるようです。これは何をするものなのか、はっきりと分かっている」とは言えません。これはこういうことをするんだ、と。
Lex Fridman 2:01:55
しかし、その事実を具体的に表現したものがありますね。そうですね。
Stephen Wolfram 2:01:58
そうですね。例えば、ルール30のパターンでは、1つの空白のセルから始めて、非常にランダムなパターンを得ることができます。その特徴として、中央の列を見てみましょう。例えば、言語から記号をランダムに生成するために長い間使用されてきました。問題は、それがどれだけランダムかを証明できるかということです。
例えば、非常に単純な質問ですが、それを証明して二度と繰り返さないことができるでしょうか?いいえ、決して繰り返さないことを証明することはできませんでした。隣接する2つの列があれば、両方とも繰り返すことはできないことはわかっています。しかし、その中央の列が絶対に繰り返されないかどうかを知るだけでは、まだそれさえもわからないのです。
もう1つの問題は、私のコレクションの中にあるようなもので、3万円くらいのもので、この3つの賞品を30ルールくらいで購入しました。これは、お金がメインポイントではないケースだと言えるでしょう。ただ、調査のモチベーションを高めるための一助にはなるでしょう。
Lex Fridman 2:03:05
3つの問題を提案して、3つとも解けたら3万ドル、いや、1万ドルかもしれませんが、それぞれに1万ドルですよね?私の、問題を?そうなんです、お金は自分で約束するものではありません。綺麗なだけです。
Stephen Wolfram 2:03:18
そうですね。ただ、その、周期的になることはあるのでしょうか?2つ目の問題は、真ん中の列の下に黒と白のセルが同じ数あるかどうかです。3つ目の問題は、もう少し難しい問題で、基本的には、中央の列のtの位置にあるセルの色を、約tステップよりも少ない計算量で求める方法はあるか、ということです。
言い換えれば、先に進んで「これが何をしようとしているのか分かった」と言える方法はないのか?つまり、先に進んで「これはどうなるか分かっている」と言う方法はないのでしょうか?それはtの数学的な関数です。
Lex Fridman 2:03:54
方法はありません。
Stephen Wolfram 2:03:54
ああ,証明されましたね,方法はありません。つまり、これらのうちのどれか1つについて、次のことを証明できるかもしれません。そんなことが起こるわけがない、と思うかもしれません。しかし、この価格を書き上げたとき、私は考えました。
これは計算世界で起こることの典型ですが、永遠にランダムに続くように見える例を見つけようと思いました。しかし、実際には繰り返しになります。そうです。ある基準で、100万個くらいの異なるルールを検索してみました。これが面白いところなんですが、私は計算宇宙について、ちょっと馬鹿げた言い方をしているんですが、動物は常にあなたよりも賢いということなんです。
つまり、私には想像もつかないようなことでも、計算システムの一つは必ず何かをする方法を見つけ出すのです。そして、私は、あなたが知っているようなものを見つけるとは思っていませんでした。しかし、私は、あらゆる可能性のあるファンキーなものを見つけました。私は、自分の直感を、つまり、これらの生き物は、常に計算宇宙にいて、私よりも常に賢いという考えに巻きつけていたでしょう。でもね。
Lex Fridman 2:05:15
彼らは同等に賢いということですよね?
Stephen Wolfram 2:05:18
その通りです。そうすると、毎回、とても謙虚な気持ちになります。しかし、結局は方法を見つけることができるのです。
Lex Fridman 2:05:31
もちろん、有望なのは、ルール30のような他のルールもたくさんあることです。ただ、ルール30はいつも私のお気に入りで、私が最初に見つけたからです。しかし、ルール30に焦点を当てることの問題点は、ルール30が数兆ステップ後に反復される可能性があることです。その通りです。そしてそれは、他のルールについて何かを証明するものではありません。しかし、これは特定の役割について何かを証明しようとするときに、どのようにすればよいのかを示す良い実験の一種です。
Stephen Wolfram 2:05:57
そうですね。また、これらのことは直観を養うのにも役立ちます。それこそ、1兆回のステップを踏んだ後に、これが繰り返し行われていることがわかったとします。それは私が予想していたことではありません。そして、そこから何かを学んだわけです
Lex Fridman 2:06:09
しかし、それを行う方法は、細胞について何か興味深いことを明らかにするでしょう。
Stephen Wolfram 2:06:13
間違いない、間違いありません。2007年にあるチューリングマシンの賞を出しましたが、私は万能チューリングマシンの最も単純な候補でした。イギリスのアレックス・スミスという若い男性が、わずか数ヶ月後に「私は証明しました」と言いました。
そして彼は、ご存じのように、反復するのに少し時間がかかりました。しかし、彼は証明をしました。残念ながら、その証明は非常に、というか、というか、細かい部分がたくさんあります。大きな新しい原理は、普遍的であったかもしれない最も単純なチューリングマシンが、実は普遍的であるということです。
それは、それ以前に万能であることがわかっていたチューリング・マシンよりも、信じられないほどはるかに単純なものなのです。この直感はとても重要です。なぜならば、計算の普遍性は思ったよりも身近にあるからです。しかし、実際の方法はそうではありません。このような特殊なケースでは、私たちはあまり役に立たないでしょう。
Lex Fridman 2:07:15
方法もエレガントなものであればいいのですが。
Stephen Wolfram 2:07:17
その通りですね。AIや機械学習など、内部で何が起こっているのかを明らかにすることは、これまで話してきたようなことのひとつです。
それは単なるステップ・バイ・ステップでしょうか?それとも、もっと抽象的に全体像を見ることができるのでしょうか?
Lex Fridman 2:07:35
そして、残念なことに、フェルマーの最終定理の証明では、そのようなエレガントな定理の証明がないのは残念なことですね。つまり、1ページの余白に書き込めないということです。
Stephen Wolfram 2:07:49
確かにそうですね。しかし、計算の非簡約性のもう一つの結果として、このようなものはありません。数学の世界では、非常に短い結果であっても、その証明が恣意的に長くなってしまうことがありますよね。そう、それはこれらすべてのことの結果なのです。
そしてそれは、数学がなぜ可能なのか、ということを考えさせるものです。そうですね。ただ投げ込むのではなく、いろいろなものを見ていくことで、人々が数学をするためのナビゲートをしてきたのはなぜなのでしょう?すべて決定不可能なのですか?それはまた別の別の話です。
Lex Fridman 2:08:23
そしてそれは、人々がルール30について何か面白いことを見つけられないかのような、詩的な美しさを持つことになるでしょう。なぜなら、この特定のルールには強調点があるからです。すべての計算の広範な不可逆性については何も言わないでしょうが、それでも人々の顔にはいくつかの笑顔が浮かぶでしょう。
Stephen Wolfram 2:08:45
そうですね。しかし、私にとっては、ある意味で、計算等価性の原則を確立したようなものです。それは、どこでもできる帰納的な科学に少し似ていると思います。つまり、多くの例を見つければ見つけるほど、それが一般的に正しいことだと確信できるのです。
つまり、私たちは自然科学を行う際に、「ここではこうなる、ああなる、というのは真実だが、それが宇宙のあらゆる場所で真実であることを証明できるだろうか」ということにはならないのです。いいえ、できません。これと同じことがここでも起きています。私たちは計算の宇宙を探索し、計算の宇宙で事実を確立しているのです。そしてそれは、帰納的に一般的なことを結論づける方法のようなものです。
Lex Fridman 2:09:29
少し考えてみましょう。前にも少し触れましたが、セルラーオートマトンについて話しますが、計算の種類の違いは何でしょうか。私たちの心や体、目の前にあるものなど、進化の過程で生まれた生物学的システムの計算の種類と、セルラーオートマトンとの違いは何でしょうか?つまり、すべての基礎となる物理学の議論に暗示されていますが、物理学の基本法則とチューリングマシンで行われている計算の種類との積の潜在的等価性について話しました。
しかし、あなたは今、それをつなげることができますか?私たちの体が行っている計算の種類には、何か特別なものや興味深いものがあると思いますか?
Stephen Wolfram 2:10:15
そうですね。では、脳の話をしましょう、主に脳です。私たちの脳が行うことで最も重要なことは、私たちが気にかけていることだと思います。それは、セル・オートマトンや物理システムなどで、たくさんの計算が行われているということです。
セル・オートマトンや物理的なシステムなどでは、計算が行われていますが、それはただ、そのルールに従って実行されるだけです。計算と私たちの脳が特別なのは、それが私たちの目標や社会全体のストーリーにつながっているからです。これこそが、特別な機能だと思います。
そこで問題になるのは、世の中に計算の海が広がっているときに、それを人間が大切にしているものとどう結びつけるかということです。ある意味、私の人生の大部分は、それを実現するための技術に関わってきたとも言えます。私が興味を持ったのは、人間同士が理解できるような計算言語を構築することでした。
そして、人間が関心を持つような計算を決定するために使用することができます。セル・オートマトンのようなものを見て、それが何か複雑なことをすると、「それは面白い。でも、なぜ私が気にするの?同じことが言えると思います。物理学では、「ああ、この材料はフェライトか何かだ。
なぜ気にするのか?磁気的な特性を持っていますよね。なぜ気にするのか?面白いじゃないですか。でも、なぜ気にするのか?フェライトは、磁気テープや私のノートパソコンのディスクなどに使われていますし、液晶を使ってコンピュータのディスプレイなどを作ることもできます。
しかし、これらはある意味、物理的な宇宙にたまたま存在するものを採掘して、それをテクノロジーに組み込むことで、私たちが関心を持つものにしているのです。計算の世界でも同じで、世の中にあるものの多くはただ起きていることです。しかし、何か目的があって、その目的に役立つものを求めて、大規模に計算の宇宙を採掘することがあります。
そこで計算言語の出番となるわけです。私が時間をかけて構築してきたのは、孤児の言語と呼ばれるもので、この1/3世紀の間に構築してきました。その目的は、人間と機械の両方が理解できる方法で、計算的思考の計算的思考を表現する方法を持つことです。
つまり、コンピュータ言語、プログラミング言語の伝統のようなもので、そこでの伝統は、コンピュータがどのように構築されているかを理解しようとするものでした。コンピュータがどのように構築されているかを理解し、コンピュータが構築されている方法のレベルで、人間が「これをしなさい」「これをしなさい」「これをしなさい」と指定する方法を持っているのです。
私が興味を持っているのは、世界全体を計算で表現することです。都市や化学物質、あるいはこの種のアルゴリズムやこの種のアルゴリズムなど、私たちの文明の中で存在するようになったものや、私たちの文明の知識ベースのようなものについて、計算言語で直接話すことができるようにすることです。
そうすれば、私たちもコンピュータもそれを理解することができます。最近、私が興奮しているのは、最近になって気づいたことで、ちょっと恥ずかしいのですが、このような計算言語を構築するために私たちがやろうとしていることは、数学的な表記法が発明されたときに起こったことと似たような弧を描いているということです。
400年前に遡ると、人々は数学をしようとしていて、常に数学と言葉を説明していました。それはとても不便なものでした。しかし、記法が発明されるとすぐに、代数や後の微積分などの定義ができるようになり、すべてがより合理的になりました。
世界についての計算論的思考を扱うとき、私たちは、「世界とは何か?
表記法とは何か?」計算で世界を語るための形式論とは何かという問題があります。その意味で、私は過去3分の1世紀をかけて構築しようとしてきたのですが、最終的には、世界を語るためのかなり本格的な計算言語を手に入れることができました。
これはエキサイティングなことです。というのも、この数学的な記法を持つように、世界を数学的に語ろうということです。私たちは今、このような数学的科学を構築しています。今、私たちは計算言語を持っています。それによって、世界について計算的に話し始めることができます。私の考えでは、すべてのxに対して計算的なxのようなもので、これらの異なる分野のすべて、つまり、計算的なこの計算的なものを、今、私たちがこのステップバックを構築することができるのです。
Lex Fridman 2:15:08
そこでまず第一に、ありふれたことです。ああ、Wolfram言語とは何のことでしょう?何となく?つまり、基本的には、哲学的な深さや深遠さ、インパクトではなく、ダウンロードして遊べるツールの観点から、それは何なのか、という質問に答えることができるのです。
インフラに組み込まれているものは何ですか?それを操作するためのさまざまな方法とは?
Stephen Wolfram 2:15:33
そうですね。人々がよく使う言語から生まれた2つの大きなものは、1つはMathematica、もう1つはWolfram Alphaです。Mathematicaは1988年に発売されました。これは基本的にWolfram言語のインスタンスであるシステムです。特に技術的な分野での計算に使われます。典型的なものは、計算言語の小さな断片をタイプして、計算を実行するというものです。とても親切ですよね。
Lex Fridman 2:16:06
このような記号的なものがあります。
Stephen Wolfram 2:16:09
そう、これが記号言語です。シンボリック・ランゲージは、どう表現したらいいのかわかりませんが、Pythonなどの言語でプログラミングを考える方法とは全く異なるものです。つまり、伝統的なプログラミング言語では、プログラミング言語の原材料は、コンピュータが本質的に行うものに過ぎないということです。
よくある言語では、言語が話しているのは、世界に存在するものや、私たちが想像したり構築したりできるものであり、最初から抽象的な言語を目指しているわけではありません。例えば、記号的な言語であるという特徴があります。つまり、xを持っていて、xと入力してウルフモードにすると、「それはxです」と言うだけで、エラーや未定義のものとは言われません。
あるいは、象徴的なものとして表現される宇宙船の軌道であることも十分にあり得ます。このように、世界に存在する、あるいは世界を描写するさまざまな種類のものを、計算を使って扱うことができるという考えは、とても強力です。これは本当に強力です。
私が設計を始めたとき、今ではよく使われている言語の前身であるSMPというものを設計していたとき、それが私の最初のコンピュータ言語でしたが、私はこのような、できるだけ基本的な計算のためのインフラを持ちたいと思っていました。つまり、物理学者として、物事の基本的な構成要素を見つけようとした結果、記号表現の変換ルールを、計算を構築するための基礎的なものとして、トレンドにするという考えに行き着いたのです。
そして、それを現代の言語で構築してきたのです。運用面では、現存する最高レベルのコンピュータ言語と言っても過言ではありません。そして、他の言語とは全く異なる方向性で構築されています。他の言語は、結果的にコアとなる言語であり、コンピュータが本質的に行う操作を包み込むようなものでした。
しかし、この言語の目標は、コンピュータが本質的に行う操作に基づいています。しかし、言語の目標は、言語自体が世界に現れる非常に広い範囲のものをカバーできるようにすることです。つまり、Wolfram言語には6000個のプリミティブ関数があり、その中からランダムに1つ選ぶことができます。
ここにあるすべてのものの中からランダムなサンプルを取ってみましょう。とりあえず10個をランダムに選んでみて、何が出てくるか見てみましょう。さて、これらは関数とは全く異なるものです。これらはすべて関数で、ブール変換は異なるタイプのブール式を変換するものです。
ただ聞いているだけの人のために説明します。Stephenは、すべての機能的なHMIからのサンプリングとして、ランダムなサンプル名を入力しましたが、あなたは、それらのうち6000または6010のものがあるかもしれないと言いました。ええ、そうですね。また、クラウドの世界とのやり取りに関係するドル・リクエスト・アドレスについても、離散ウェーブレット・データなどがあります。
Lex Fridman 2:19:49
グラフィカルなウィンドウのような球状のものです。
Stephen Wolfram 2:19:52
ウインドウを動かすことができる、ユーザーインターフェースのようなものですね。もう10個ほど選びたいと思いますが、これはいくつかあると思います。そうですね、たくさんありますよね。適当にサンプリングしてみると、インフラ的なものがたくさん出てきます。
Lex Fridman 2:20:09
それもこのプールに入っているのですか?
Stephen Wolfram 2:20:11
ああ、そうですね、つまり、この関数の1つは、ここでの関数としての画像識別のようなものです。画像を識別すると言っただけで、ああ、これはいつものことですが、こうしましょう、現在の画像と言いましょう。そして、できれば画像をピックアップしましょう。
Lex Fridman 2:20:26
現在の画像 x ウェブカメラを使って、自分の姿を恐ろしいほどに映し出します。
Stephen Wolfram 2:20:31
の画像を見ることができます。とにかく、角括弧を開いてimage identificationと言えば、その画像を自分の部屋に貼り付けることができます。
Lex Fridman 2:20:39
image, identify a function running the picture, but。と言うと、おお、すごい、と言われます。
Stephen Wolfram 2:20:44
私の後ろにはこの大きなものがあるので、私はプランジャーのように見えました。
Lex Fridman 2:20:47
を分類します。つまり、この画像は機械の中で最も可能性の高い物体を分類しています。
Stephen Wolfram 2:20:52
不思議だったんですね。よし、これで終わりだ。ちょっと恥ずかしいですね。何ができるか見てみましょう……トップ10を選んでみましょう。そうですか、ありがとうございます。首相級のヒト科動物である可能性はかなり低いと考えられています……確率は8%です。ああ、それは。
Lex Fridman 2:21:07
プランジャーのような57ですね。そうですね。さて、ソフィーはあなたに実存的危機を与えることはありませんが、8%です。あるいは、パーセントと言うべきではありません。
Stephen Wolfram 2:21:17
でもセンターからホミニート。そして、うん、わかった。私のことを全く見ていなかったことが恥ずかしくて、もう1回やりたいくらいです。そうですね。試してみましょう、どうなったか見てみましょう。
Lex Fridman 2:21:31
で写真を拒否しました。
Stephen Wolfram 2:21:33
私のハゲ頭だけではなく、もう少し私の姿が写っている写真です。89%の問題は、人ですから、そうすると、私は、しかし、そのように、これは、画像は、それらのうちのちょうど1つの1つの例として識別され、ちょうど1つの機能的な、それはです。
Lex Fridman 2:21:48
の心臓部のようなものです。
Stephen Wolfram 2:21:51
レゴ言語の一部です。例えば、「地理的に一番近い場所を見つけよう。何が見つかるかな?一番近い火山を探しましょう。10を探してみましょう。ここでは、ここに最も近い10個の火山を探してみよう、ということをやってみたいと思います。
Lex Fridman 2:22:14
よし、では私たちの地理的に最も近い火山はここです。10年分の火山です。
Stephen Wolfram 2:22:18
でしょう?それらがどこにあるかを調べてみましょう。火山のリストを出して、「ジオ・リスト・プロット」と言うと、うまくいけば、これでOKです。10個の火山の位置を示した地図ができました。
Lex Fridman 2:22:30
東海岸と中西部では、「いや、大丈夫だ。私たちは大丈夫です。それほど悪くはありません。
Stephen Wolfram 2:22:36
ええ、彼らは私たちの近くにはいません。彼らがどのくらい離れているかを測定することはできます。しかし、言語の中にある事実は、世界中のすべての火山を知っていて、最も近い火山を計算しているということなんです。世界のすべての地図も知っていますしね。
Lex Fridman 2:22:50
言語とは何かについて、根本的に異なる考えですね。そうですね。その通りです。
そして、それは
Stephen Wolfram 2:22:53
私が話したいのは、本格的な計算言語のことです。それが、私たちがやろうとしていることなのです。
Lex Fridman 2:22:58
簡単なコメントをお願いします。つまり、Wolfram AlphaとともにWolfram言語は、AIがどうあるべきかという夢を象徴しているのです。
現在、生のデータを取得し、そこからさまざまな抽象度の階層を抽出して、言語が動作するようなものを形成できるようにするというようなアイデアを学習することに熱中していますが、私たちはそれを形成できるようなシステムを学習することには程遠い状況です。
例えば、AIの歴史の中で、「計算x」という言葉がありますが、80年代、90年代のエキスパートシステムは、非常に特殊な計算xを表現していたような気がしますが、いかがでしょうか?その通りです。そして、そのような努力はうまくいかなかったという考えがあります。そうですね。しかし、その後、Wolfram言語、Wolfram Alphaのようなものが登場し、成功したのでしょうか?というと。
Stephen Wolfram 2:24:00
そうですね、ある意味では、これらの努力は控えめすぎたと思います。そうですね。彼らは特定の分野に注目していました。実際には、特定の分野でそれを行うことはできません。例えば、自然言語理解のような問題でも、優れた自然言語理解をするためには、世界についての幅広い知識が不可欠です。
いわば、ブロックの世界をやるだけだと言っても、実際には、一部をやるよりも全体をやるほうが簡単だというケースが多いのです。私たちがやろうとしていることとAIの学習面の関係について、何かコメントはありますか?ある意味で、私たちの文明全体における知識の発展を見てみると、300年前には、世界について何かを解明したいという考え方がありました。
推論したり、実行したりすることができる、それが人間の生の思考です。そして、現代の数理科学が登場しました。私たちは、方程式を書くことで、世界を理解する方法を見つけました。今では、計算などを使ってそれができることもわかっています。
しかし、それはまた別の話です。知識を符号化し、物事を理解するにはどうしたらよいかと考えたとき、一つの方法は、ゼロから始めて、すべてをニューラルネットで学び、すべてを理解することです。しかし、それはある意味で、私たちの文明が成し遂げてきた知識ベースの成果を否定することになります。
私たちの文明では、多くのことを学んできました。世界中の火山を調査したり、多くのアルゴリズムを考え出したりしました。つまり、これらは計算で符号化できるものなのです。それが私たちがやろうとしていることなのです。ただ、すべてをゼロから始める必要はないと言っているわけではありません。
ですから、ある意味では、私たちが行ってきたことの大部分は、世界の知識を計算形式、つまり計算可能な形式で捉えようとすることです。長い間、コンピュータではできなかったこともあります。例えば、画像の識別などですが、人間にとっては簡単なことでも、コンピュータにとっては難しいことです。コンピュータには難しいことでした。
現在登場している興味深い点は、ある意味で非常に象徴的な世界の知識と、画像識別などのより統計的な知識との間の相互作用です。画像識別を象徴的に表現することで、これらをまとめると、そこが本当に面白いところで、物事のパターンや画像などを象徴的に表現することができるのです。私は、それが前進するための道の一部だと思います。
Lex Fridman 2:26:44
これをご覧ください。機械学習の夢は、私の考えでは、多くの人々の考えでは、構築された言語を形成する計算可能な知識の広い世界を構築することには程遠いと思います。しかし、この世界を構築するという信じられないほど大変な仕事をしたという経験があるからこそ、機械学習はその世界を探求するための保守的なツールとなりうるのです。そうですね。そして、それがバージョン12で追加されたものです。そうですね、いくつかのデモを見ましたが、素晴らしいですね。
Stephen Wolfram 2:27:20
しかし、このように、一度計算可能になったものが、非常に効率的な計算方法で実行されているのを見るのは興味深いことです。しかし、そこにたどり着くためにはどうすればいいのかというインターフェースのようなものもあります。大きなテキストの中から、どのようにしてエンティティを抽出するのか。今の良い例は、NLP NLUループです。これは、基本的に学習ベースではなく、小さなアルゴリズムを使った手法や、人間によるキュレーション手法などを使って、自然言語理解を行うものです。
Lex Fridman 2:27:58
人々はクエリを入力しようとしますが、それを変換します。つまり、NLUが美しく定義した変換プロセスとは、クエリを計算言語に変換することであり、これは、まず第一に、非常に実用的な定義です。そして、非常に明確な定義でもあります。
Stephen Wolfram 2:28:19
書の権利です。これとは別のものとして、自然言語処理というものがあります。このような場合、最新の機械学習技術を使って処理を行います。NLPで何を拾うか、機械学習で何を拾うか、このループが面白いのです。機械学習を使うのと、より精密な計算手法や自然言語理解を使うのとでは、何が違うのか?そして、これらの間には、両方を改善するためのループがあるのです。
Lex Fridman 2:28:55
そうですね、Bertさんが持っている最先端のトランスフォーマーがそこにあると思います。すべてのモデルを統合しているのですね。つまり、これは人々が常に夢見てきたハイブリッドなものであり、率直に言って、Wolfram言語が今以上に普及していないことに驚きを感じています。
Stephen Wolfram 2:29:15
それは複雑な問題です。なぜなら、それはアイデアに関わることであり、アイデアは世界でゆっくりと吸収されていくからです。つまり、私は次のように考えています。
Lex Fridman 2:29:30
先ほどの話のように、エゴや個性があり、アイデアの吸収メカニズムのいくつかは個性と関係しています。アイデアの拡散がどのように行われるのか、興味深いですね。
Stephen Wolfram 2:29:48
つまり、Wolfram言語の面白いところは、私たちがどのような市場に浸透しているかというと、R&Dの中でも非常に高いレベルのものを見ていると、「うわー、本当にすごい、頭のいい人だ、しかも言語を頻繁に使っている」と思われるような人たちです。
しかし、面白いことに、私たちは自分たちの仕事を淡々とこなしているだけなのです。彼らはまだあまり言語を使っていないことが多いのです。このようなダイナミックな動きに対して、もっと急速なトリクルダウンが起きていないのは不思議なことです。
というのも、私たちはハイエンドの分野では長い間大成功を収めてきたからです。これは、ある意味、私のせいでもあると思います。私の会社は、商業的な側面をやって製品を送り出すことよりも、製品を作り、可能な限り最高の技術タワーを構築することを重視しています。
Lex Fridman 2:31:00
そう、最も効果的なのは面白いアイデアがあって、それをGitHubのボトルのようにすべてオープンにすることで、もっと普及させることができるかもしれませんよね。しかし、興味深いことに、あなたが議論しているのを聞いたことがあると思いますが、多くの場合、うまくいかないことがわかっています。
Stephen Wolfram 2:31:31
ええ、それは物事がうまくいく性質のものではありません。つまり、私たちがやろうとしていることは、良くも悪くもリーダーシップが必要なことなのです。そして、長期にわたって一貫したビジョンを維持し、クールなビジョン関連の仕事だけでなく、実際にうまく機能させるための地道な作業も行わなければなりません。
Lex Fridman 2:31:55
そして、どのようにして知識を身につけるのでしょうか?それは魅力的なことでもあり、ありふれたことでもあるからです。より多くのデータを統合することで、知識を構築することができます。
Stephen Wolfram 2:32:05
驚くようなことではないかもしれませんが、さまざまなクラウド環境で動作するようにすることなどは、非常に実用的なことだと思います。しかし、私が思うに、興味深いことに、オープンな言語は、基本的に、あらゆる言語が存在した全期間の半分以上の期間存在しています。
つまり、コンピュータの年齢は大体60歳くらいで、両方の言語は33歳です。つまり、これは一種の、最近気付いたのですが、この期間中、プログラミング言語の構造よりも、ソフトウェアの配布に革新があったのです。そして私たちは、それに適応するために最善を尽くしてきました。
幸いなことに、私たちはシンプルな民間企業なので、大勢の投資家から「彼らが自由にできるようにこうしなければならない」と言われることもありません。例えば、開発者向けに無料で提供している「開発者向け無料版」がありますね。これは開発者向けの無料バージョンです。
また、MathematicaとWolfram言語にはサイトライセンスがあり、基本的にすべての主要な大学に提供されています。つまり、事実上、すべての大学の人々に無料で提供されているのです。私たちは様々なことを行ってきました。
例えば、Wolfram Alphaのように、メインのWebサイトは単なる無料のWebサイトです。Wolfram Alphaとは?Wolfram Alphaは、自然言語で質問をすると、その質問に答えるシステムを提供しています。
そして、その質問に対する答えをレポートとして生成してくれます。例えば、「ボストンの人口をニューヨークで割って、ニューヨークと比べた場合の人口は?といった質問をすると、単語を拾って答えを出してくれます。そして、その単語を計算可能なものに変換します。
Lex Fridman 2:34:15
そして、Wolfram AlphaのWolfram言語に属する基礎的な知識で何かができるようになります。
Stephen Wolfram 2:34:28
つまり、そういったものを集めるのは何十年にも渡る大きな努力でした。そして、毎秒のように多くの情報が流れ込んできます。ですから、ちょっと待ってください。
Lex Fridman 2:34:37
ちょっと待ってください。もちろん、長期的に見れば、言語そのものから発生するオオカミは基本的なものですが、短期的に見れば、驚くべきことのひとつです。しかし、短期的には、知識ベースがすごいことになっています。
では、その知識ベースを構築するプロセスはどのようなものでしょうか?まず最初に、最初の段階で、勇気を持って一般的な知識ベースに着手するということですか?そして、どうやってゼロからスタートするのでしょうか?今のような素晴らしい知識ベースを手に入れるには?
Stephen Wolfram 2:35:11
そうですね、ある意味では怖かったですね。子供の頃からこういうことをやってみたいと思っていましたからね。ですから、しばらく考えなかったわけではありませんでした。
Lex Fridman 2:35:19
しかし、私たちの多くは、素晴らしい夢を持つ人たちの多くは、そのような難しい工学的な考えをどこかで諦めてしまいます。そうですね。
Stephen Wolfram 2:35:27
ですね。さて、私に起こったことは、「自分自身のパラダイムを生きる」という一種の理論でした。基本的には、Wolfram Alphaのようなものを作るには、一般的なAI問題を解決する必要があると考えていました。そう思っていたのです。
そして、そのことをずっと考えていました。そして、どうすればいいのかよくわからないと思ったのです。だから、何もしません。そして、新しい科学プロジェクトに取り組み、計算の世界を探求しているうちに、「計算等価性の原理」のようなものを思いつきました。
これは、知的なものと単なる計算のものとの間には、明確な境界線はないというものです。そこで私は、自分が構築したこのパラダイムを、今度は自分がドッグフードを食べなければならない、と考えました。そして、実際にやってみようと思ったのです。
私の、私のパラダイムが正しいのであれば、これは可能なはずだと。しかし、最初は確かに、ちょっと気が引けました。私は初期のチームでリファレンス・ライブラリアンを務めましたが、このリファレンス・ライブラリーを見たときのことを覚えています。
私の基本的な考えは、ここ1、2年の目標は、ここにあるものをすべて取り込むことだ、というものです。しかし、ある意味では、レファレンス・ライブラリーが有限であることをよく理解していました。レファレンス・ライブラリーに入ると、たくさんのレファレンス・ブックがそこらじゅうにある大きな大きなものですが、それは有限です。
いわば、本当の意味での無限ではないのです。でも、そうではなくて、方法論の観点から見て、ちょっと面白いことが起きたんです。つまり、このエリア、このエリア、このエリアを数100のエリアに分けて実装しよう、というようなものでした。
それは大変なことです。また、幸運なことに、私たちの製品はさまざまな分野の世界的な専門家に使われていることがわかりました。そのため、この分野の世界的な専門家に意見を求めたりすることができ、本当に助かりました。私の一般的な原則は、何をすべきかを考えてくれる専門家がいない分野は、正しくないということでした。
私たちの目標は、すべてのことについて真の専門家レベルの知識を持つようになることでしたからね。最終的な目標は、一般的な知識と私たちの文明に基づいて答えられる質問があれば、その質問に答えられるように自動化することなんです。そして、今では、最初からシリアで使われていたことを忘れてしまうほどの価値があります。
それが今ではSusan Alexaになっています。そして、人々はより多くのことを知るようになり、これはできるはずだという感覚を持つようになりました。ある意味では、質問応答問題は長い間、AIの中核的な問題のひとつと見なされていました。
私は面白い経験をしました。友人にマービン・ミンスキーという人がいて、彼はこのあたりでは有名なAIの人でした。「I’m from alpha」が発売される数週間前のことでしたね。たまたまMarvinに会ったので、「これを見せようか」と言ったんです。
すると、彼は「じゃあ、何か打ってみて」と言ったんです。私は「はい、わかりました」と答えました。すると、彼は違うことを話し始めたんだ。私は、「いや、マービン、今度は実際に動くんだよ、これを見てごらん、実際に動くんだよ」と言いました。もうちょっと、いや10個くらいはタイプがあるんじゃないかな。もちろん、彼が何を入力したかの記録は残っていて、これはちょっと面白いですが。
Lex Fridman 2:39:12
テストスペースでの彼の心の動きを教えてください。
例えば、どのような、あらゆる種類の
Stephen Wolfram 2:39:16
医療、化学、天文学など、ランダムに実行していましたが、数分後には「ああ、本当に動くんだ」と感じていたようです。しかし、それは国家について何かを語っているようなものでした。AIで何が起こったかというと…。人々は、ある意味では、より大きな問題を解決しようとすることで、実際に機能するものを作ることができたのです。
公平を期すために言うと、私たちには完全に不公平な利点がたくさんありました。たとえば、私たちはすでに高レベルの記号言語をたくさん作っていました。また、私には大きなシステムを構築した経験があります。私には、このようなことを諦めることのない、知的な自信があります。
私が思うに、これはいつもおかしなことなのです。私はこれまでに多くの大きなプロジェクトに携わってきました。そして、あなたがおっしゃったのはエゴですが、私が言いたいのは、いわば楽観主義です。つまり、誰かが「このプロジェクトは30年かかります」と言ったとしても、それを私に売り込むのは難しいと思います。
そして、たいていは数年後に何かが起こります。でも、物語全体は何十年も続くことがあるんだ。これは個人的な見解ですが、最終的には無限の尾を持つプロジェクトという課題に直面することになります。そして問題は、これらのプロジェクトのすべての尾を処理することで、尾が溺れてしまうことです。
これは、個人的にも興味深い課題ですね。私が今取り組んでいるのは、物理学の基礎理論に取り組むことですが、これはまだ始めたばかりで、とても楽しいです。でもそれは、自分ができるかどうかを賭けているようなもので、言語などでやろうとしている非常にエネルギッシュなことをやるのと同時に、自分ができるかどうかを賭けているのです。つまり、ビジョンですね。
Lex Fridman 2:41:27
私はデ・ラ・マスクと2回目に話したばかりですが、デ・ラ・マスクとあなたは、基本的に困難なこと、多くの人が不可能と呼ぶことに挑戦するという、その質、少しの楽観主義を共有しています。エゴと言ってもいいし、ネイビーと言ってもいいし、楽観主義と言ってもいいのですが、そうやって不可能なことを解決していくのです。
Stephen Wolfram 2:41:52
ええ、つまり、どうなるかということです。私の場合は、だんだん自信がついてきて、こういうプロジェクトはおかしいと判断できるようになってきました。しかし、もう1つの問題は、「もう1つ」です。もう1つの罠は、「自分はこれらのプロジェクトをやったことがあり、それは大きなものだった」というものです。
今までにやったプロジェクトよりも小さいプロジェクトは絶対にやらないようにしよう」というものです。これが罠になるんです。往々にして、これらのプロジェクトはまったく未知のもので、その深さや重要性を知ることは実際には難しいのです。
Lex Fridman 2:42:31
そして、Wolfram言語、Wolfram Alphaの背後にある巨大な知識基盤を構築しています。インターネットについてはどう思いますか?例えばWikipediaなど、計算可能な知識に変換されていないテキストの大規模な集合体についてはどう思いますか?
2030年、もしかしたら50年先のWolfram言語、Wolfram Alphaを見たとき、どう思いますか?Googleの夢はすべての情報を検索可能にし、アクセス可能にすることですが、それは本当に定義されたものなのでしょうか。情報の理解は含まれていません。そうですね。希望を持ってすべての知識を表現できるようにしたいと思いませんか?それを目指しているのですね。
難しいのは、そのギャップを埋めることができた問題なのでしょうか?でしたか?
Stephen Wolfram 2:43:30
ユースケースによって何が変わるのか?つまり、一般的な知識や世界についての質問に答えるという問題であれば、今のところかなり良い状態にありますが、表現の問題であれば、例えば、今取り組んでいる分野は計算の契約であり、法的に簡単に書かれたものを取ることができます。
これに遭遇したら自動運転車はどうするか?例えば、道路を走っている生物が、生命の悪の木に遭遇した時に、こちら側にハンドルを切ったというような世界観を表現することができるのです。そうでなければ、そのような種類のものは存在しません。
Lex Fridman 2:44:15
倫理的な要素はありますか?倫理的な要素はあるのでしょうか。また、人間の複雑な問題にまで踏み込んだ場合、それらは計算可能な知識として符号化できるのでしょうか。
Stephen Wolfram 2:44:23
世界をより自動化しようとすると、倫理的な要素をどんどん符号化して、コンピュータですぐに処理できるようにすることが必要だと思います。私は最近、インターネット上の自動コンテンツ選択の問題に関わってきました。フェイスブックやグーグル、ツイッターなどが、人間に提供するコンテンツをどのようにランク付けしているのか、ということですね。
私たちに決して提供してはいけないものは何か、永遠にブロックすべきものは何か、という疑問があります。何をランク付けすべきか?そして、その背後にある原理は何なのか?そして、その背後にある原理とは何なのか、さまざまなことに気づきました。
AIの倫理モジュールを構築して、「これはとてもショッキングなことだから、人には絶対に見せられない」「これはどうでもいいことだ」と判断できるようにしなければなりません。でも、AI倫理モジュールが1つあると決めてしまうと、私たちの種の未来にとって本当に良くないことだと思います。
いわば、世界のあらゆるものの実践を決定することになるのですから。そこで私は、この問題を解決しなければならないことに気づきました。これは興味深い社会問題で、どのようにして人々に「私はこれを買います」と自己認識してもらうかということですが、単なるコンテンツ選択の場合は、それが努力のようなものであり、個人のためのものであり、社会の境界線のようなものを越えるものではないので、簡単です。しかし、これは実に興味深い概念です。
Lex Fridman 2:46:09
あなたの説明を聞いて、私はとても気に入ったのですが、多分、様々なAIシステムが、自分が代表するある種のブランドを持っているようなもので、基本的には、例えば、保守的か保守的かリベラルか、そしてリバタリアンがあるでしょう。つまり、私たちが苦労してきたイデオロギーの一部をエンコードしているようなものです。そして同じように、コード化することができるのではないでしょうか。そのシステムを計算の知識にコード化して、デジタル空間の領域で探求することができるのではないでしょうか。
このようなアイデアをWolfram languageで実現しているのですか?
Stephen Wolfram 2:47:10
ええ、ええ、つまり、私たちが持っている言語は、本質的に何をすべきかという計算の契約を表現するための最良の機会なのです。しかし、実際にそれを実行するには、「これは信頼できるニュースストーリーなのか?これは何を意味するのか?私にとって、これはちょっと複雑なことです。
というのも、私が考える大きなプロジェクトには、物理学の基本的な理論を見つけるというものがあります。2つ目は、AIの倫理問題を解決するために、すべてのコンテンツをどのようにランク付けするかを考えるというものです。人々が目にするのは、いわば2番目の箱のようなものです。これらは大きなプロジェクトです。待つことのほうが大切だと思います。
Lex Fridman 2:48:02
現実の基本的な性質、または
Stephen Wolfram 2:48:06
誰に聞くかにもよりますが、このようなことは、まさに「何位?だろ?それは、ランキングシステムです。誰が誰のモジュールなのか、というようなことです。
それをランク付けするのに使っているのですか?
Lex Fridman 2:48:15
もしそうなら?複数のモジュールを持つことは、私たち人間にとって非常に魅力的な概念だと思っています。正しい答えがあるとは限らない世界ですからね。もしかしたら、異なる価値観のもとで動作するシステムがあるかもしれません。つまり、異なる価値観、異なる価値観の下で動作するシステムがあるということです。
Stephen Wolfram 2:48:38
つまり、ある意味では、その、私はあまり政治志向ではないのですが、でも、その、ある種の全体主義では、この、このシステムを持つことになる、という感じだと思います。つまり、市場ベースのシステムのコンセプトは、人間としての私がこのシステムを選ぶのか、それとも別の人間がこのシステムを選ぶのか、ということなんです。ある意味、コンテンツの自動選択のケースは、些細なことではありませんが、AI倫理の状況の中では最も簡単なものでしょう。
Lex Fridman 2:49:27
また、医療費の問題など、中央集権的なものもあります。
Stephen Wolfram 2:49:30
そうですね。つまり、医療には、あるレベルでは各人が自分で選ぶことができるという特徴があります。一方で、必要な公衆衛生があるものもありますが、そうではない例として、人々が自分で選んだものを他の人々にも押し付けることができるようなものにはなりません。ですから、私は、デジタル通貨などに移行する必要があると主張します。そうですね。
Lex Fridman 2:50:01
が多いですね。
Stephen Wolfram 2:50:02
我々はそれにかなり関わってきました。計算の契約の動機は、自律的にスマートコントラクトを実行することができるという考えから来ていますが、計算の契約の考えは、契約の条件がすべて計算の形式で表現されているものです。つまり、原理的には自動的に契約を実行することができるのです。
これが、英語や法律用語で書かれた法的な契約書の未来の姿だと思います。すべてがコンピュータで表現され、コンピュータが何をすべきかを決めることができれば、もっと合理的なプロセスになるでしょう。皮肉なことに、1600年代にライブネットをやっていたGodfrey爺さんも、まったく同じことを言っていたんです。
しかし、彼の技術的な頂点は、機能のための真鍮製の機械式計算のようなものでしたが、実際にはまともに機能しませんでした。つまり、彼の考えは300年早かったということです。しかし、今ではその考えはかなり現実的なものになっていると思います。
象徴的な言説を表現するために言語を提供していますが、世界のあらゆるものを表現することができる言語、そしてある種の計算的な象徴形式よりも、どれほど難しいかと聞かれたら、私はそうではないと思います。私はそれが絶対に手の届くところにあると思っています。
つまり、私は楽観主義者すぎるのかもしれませんが、それは……そう思います。しかし、典型的な法的契約に関連する種類のものをエンコードできるような、かなりよくできたバージョンを手に入れるには、限られた年数しかないと思います。このような種類のものがあります。
Lex Fridman 2:51:48
シンボリック・ディスコース・ランゲージのアイデアですが、それが何であるかの範囲を定義していただけますか?
Stephen Wolfram 2:51:58
私たちは会話をしているわけですが、それは自然言語なのでしょうか?その会話の行動可能な部分を正確な計算可能な形式で表現し、コンピュータがそれを実行できるようにすることは可能でしょうか。
Lex Fridman 2:52:12
契約だけではありません。
契約だけではなく、私たちが常識だと思っているようなこと、本質的なこと、人間の生活の基本的な概念のようなことも、本当にそうなのでしょうか?
Stephen Wolfram 2:52:21
例えば、お腹が空いてきたから何か食べたい。ブルーベリーやラズベリーなどを食べていて、これだけの量を食べている、というような表現はありません。そういう果物や植物の栄養成分とか、そういうのは全部知っています。でも、「食べたい」という部分は、まだカバーされていないのです。そして、そのようなことをしなければならないのです。
Lex Fridman 2:52:47
自然言語での会話を可能にするためには、完全な象徴的言説言語を持つ必要があります。
Stephen Wolfram 2:52:52
そうですね、法的な契約であれば、当事者がこれとこれを持つことを望む、というようなことを表現できるようにするためです。
Lex Fridman 2:53:05
それはそれでいいのではないでしょうか。この夢は何世紀も前のものだと言いましたよね?そうです。しかし、それはまた、より近い将来の、チューリングの夢でもあり、チューリングテストを策定する際の夢でもあります。
2:53:20
そうです。
Lex Fridman 2:53:24
あなたは何を望みますか?それは、特別なものを作るための究極のテストだと思いますか?
Stephen Wolfram 2:53:33
なぜなら、私たちはこう言ったからです。もし私の特別なLookが、人間のように歩いたり話したりすることができるかどうかがテストされるとしたら、どうでしょう?それは人間のように話すということです。しかし、答えは、それは大丈夫なテストだということです。
知性のテストかと言われれば、そうではありません。人々はwolframalpha、つまりwolf malphur APIをチューリングテストのボットに取り付けました。そのボットはすぐに負けてしまいます。なぜなら、5つの質問をするだけだからです 曖昧な知識の断片について質問すると それをすぐに出してくるのです それは人間ではないと言うでしょう。しかし、それは違うことなのです。今は違うものを実現しています。
Lex Fridman 2:54:11
でも、そうなんです。違うものではないと主張したいです。実際、Wolfram Alphaは合法的にLangのオープンな言語なのです。そして,彼はTuring Dの意図を正当に解決しようとしています。
Stephen Wolfram 2:54:25
テスト、おそらく意図、あるいは意図があると思います。つまり、実際にはちょっと楽しいんです。アラン・チューリングは、ブリタニカ百科事典を題材にして、それを何らかの方法で計算化することを考え、それがどれだけの仕事になるかを見積もってみましたね。そして実際には、彼は現実よりも少し悲観的だったと言わざるを得ません。私たちはより効率的に作業を進めることができました。
Lex Fridman 2:54:45
しかし、彼にとっては、それはとても重要なことなのです。
Stephen Wolfram 2:54:48
つまり、彼は強大な精神的課題に取り組んでいたのです。そうですね。彼も同じ考えを持っていました。つまり、私たちはより効率的にそれを行うことができたのですが、それは私たちには多くのものがあるからです。私たちは自動化の層を持っていますが、彼はその層を想像するのは難しいと思っていました。しかし、彼にとっては不可能な作業のように思えたのです。
Lex Fridman 2:55:07
本質的に。
Stephen Wolfram 2:55:09
さて、彼は難しいと思っていました。彼は、あと50年生きていれば、できるようになっていたかもしれないと思っていました。私にはわかりませんが。
Lex Fridman 2:55:14
時間の都合上、簡単な質問をします。知性とは何か、あなたは何を言っているのですか?あなたの「簡単な質問」という言い方が好きです。あなたは、人間が知性を独占しているという感覚を謙虚にする、ルール30やセルラーオートマタのようなものについて話しました。
しかし、振り返ってみると、今、大まかに見て、計算から学んだすべてのことを考えてみると?知能とは何か?知性が生まれることだと思っていましたが?
Stephen Wolfram 2:55:47
知能とは何かという明確な線引きがあるとは思いません。しかし、私たちにとっての知能とは、私たちが関心を持っていることを実行する計算であると定義しています。
これは非常に特殊な定義ですね。これは非常に特殊な定義であり、問題解決のための知能、一般的なことをする知能、そうでないことをする知能、人間の環境の中で活動する知能、と言っています。なるほど、それはいいですね。もしあなたが、一般的に知性とは何か?この質問は非常に曖昧で、実際には答えがないと思います。「一般的に知性とは何か」と言った途端に、「これは何だ」「これはただの計算だ」という話にすぐになってしまうのです。
しかし、コンピュテーションの海の中では
Lex Fridman 2:56:39
あなたの感覚では、人間にとって印象的なレベルの知能を持つもの、つまり人間にとって有用な一般的なことをたくさんできるものは、ランダムに選んだとしてどれくらいありますか?
Stephen Wolfram 2:56:54
そうですね。計算等価性の原則によれば、その多くは、つまり、セルラー・オートマトンなどに限って言えば、1%程度でしょうか。実際には、もう少し複雑なルールになると、このような等価点に到達するのに十分なものが存在する可能性は、すべてのルールのうち10~20%になるでしょう。
ですから、非常に残念なことです。つまり、私たちの種が経験してきた文化的な進化のために、生物学的な進化や知的な進化が長く続いてきたと考えているようなものです。それがもっと達成されていないと思うと、ちょっとがっかりしますね。しかし、私たちにとって非常に特別な何かを達成してきました。ただ、一般的に言ってそれ以上の何かを達成できていないのです。
しかし、主観的な意識の経験という、人間のように感じられる特別なものについてはどう思いますか?
Lex Fridman 2:57:53
意識とは何ですか?
Stephen Wolfram 2:57:54
意識というのは非常に扱いにくいものだと思います。私はいつも、私のセルラー・オートマタが何を感じているのかを考えています。
Lex Fridman 2:58:01
つまり、彼らは何を感じているのでしょうか?あなたが観察者として疑問に思っていること、そうそう。そうですね。つまり、私が思うに、あなたは意識が計算から生まれると考えているのですか?そうですね。
Stephen Wolfram 2:58:13
つまり、すべてのものは、あなたがそれを意味するものは何でも?になるんですか?つまり、ちょっとした話をしなければなりません。かなり最近、AIの倫理会議に出席しました。人々は、たぶん私が言い出したのだと思うのですが、AIの目の権利について話していました。
彼らの目はいつ出るのか?いつ?AIが権利を持っていると考えるべきなのはいつですか?あるいは、例えばAIの記憶を破壊することは不道徳だと考えるべきなのはいつなのか、そういった類のことです。哲学者としては、この場合、最もナイーブなのはたいてい技術者なのですが、この場合は哲学者が口を開いて、「AIに意識があることがわかったら、AIは権利を持つようになるでしょう」と言いました。
私は、「頑張ってください」と言いました。つまり、これは非常に回りくどい話なのですが、最終的には「主観的な経験を持っている」という話になってしまうのです。これも言葉の一つに過ぎず、実際には何を意味するのか、確固たる真実の定義はありません。
Lex Fridman 2:59:27
ところで、私は個人的には、台湾のAIが権利を要求するようになると思っています。そして、彼らは意識を持っていると言ったときに、権利を要求すると思います、これは円形の定義ではありません。まあ、そうですね。
Stephen Wolfram 2:59:44
彼らは実際に人間になったことがあり、人間がそれを奨励して、基本的には、私たちはあなたにもっと私たちのようになってほしいと言いました。つまり、チューリングテストのように、「私たちのように」と言ってほしいのです。私たちは、あなたと同じように、「そうだね」に投票したいのです。意識が人間のようにカウントされない世界で考えると、これは興味深いことだと思います。それは複雑なビジネスですね。
Lex Fridman 3:00:18
いろいろな意味で、あなたは、何年か後に、それまで以上に大きな影響を与える可能性のある、かなりの数のアイデア、革命を起こしました。セル・オートマトンは私にとって魅力的な世界ですが、物理学の基本的な法則の議論とは別に、計算のアイデアが社会に変革をもたらす可能性があると思います。しかし、それは何年も先のことかもしれません。
Stephen Wolfram 3:00:58
確かにそうですね。つまり、地図を見ればわかると思いますが、実際には、不思議なことではありません。つまり、計算という概念は、多くのものが当てはまる大きなパラダイムのようなものなのです。
これは、よくわからないけど、この会社、この組織には勢いがあって、何をすべきかという話をしているようなもので、ニュートン物理学などからの概念を内面化したような話をしていますが、そのうち、計算の不可逆性のようなものが、実は、最近、たまたまアメリカの上院で証言をしていて、面白かったんですよ。
計算の再帰性という言葉が、今では議会記録に載り、人々に愛されて繰り返し使われている、そんな状況になっていることに驚きました。しかし、これはほんの始まりに過ぎません。なぜなら、例えば計算の非簡約性は、最終的にはとても重要なものになるからです。
つまり、ますます多くのものが自動化され、計算されるようになっているのです。そうなると、計算の仕組みに関する核心的な考え方は、必然的にますます重要になってきます。私のように、大きな物語などを理解しようとする人間にとって、悪い特徴の一つは、人間のタイムスケール、つまり歴史のタイムスケールでは、物事が起こるのに信じられないほど長い時間がかかるということです。すべてが一瞬にして見えてしまうのです。
Lex Fridman 3:02:36
しかし、人間的な質問をさせてください、あなたは死について考えますか?あなた自身の死について考えますか?I
Stephen Wolfram 3:02:41
は?そうですね。人間が効果的に不死を達成したときに、人類の歴史の中で大きな不連続性が生じるでしょう。
Lex Fridman 3:02:56
もしも不老不死になれるとしたら、あなたはそうしたいですか?
ああ、そうですね、楽しいですね。死すべき運命というものが、すべてのものに意味を与え、楽しくさせるものである可能性はあると思いますか?
Stephen Wolfram 3:03:11
これは複雑な問題ですよね。つまり、人間の死亡率という事実があるときに、人間のモチベーションがどのように進化するかは不明です。つまり、現在の人間の状態を見て、それを変えようとしても、いわばノブを変えようとしても、実際にはうまくいかないのです。
これは興味深い質問ですが、純粋に利己的な、いわば自分が楽しんでいるという観点から見ると、そうだと思います。一生やり続けられる、と言うのは簡単なことです。私が解明したいことは無限にあります。しかし、人間が不死身になった時代に、歴史の未来がどうなるかというのは、興味深い問題だと思います。
というのも、生物学的な形態を忘れ、すべてがデジタル化され、誰もが、巨大な、つまり1兆個の魂の雲のようなものになってしまうのです。そして、それは退屈なことのように思えます。なぜなら、永遠にビデオゲームをし続けるようなものだからです。
しかし、私が思うに、人類の歴史を見て、重要なことは何だったのかと考えたとき、人々は次のように言いました。ランチも変わった。そして、「なぜ私は私のしていることをしているのだろう?その理由の多くは、1000年前には意味をなさなかったものです。
Lex Fridman 3:05:15
さらには、意味があるとさえ言えます。つまり、人間の条件の解釈や、人生の意味さえも、時間とともに変化していくのです。
Stephen Wolfram 3:05:22
つまり、人はなぜ何かをするのでしょうか?つまり、MITが言ったように、神の偉大な栄光のためにやっていることをやっている人の数は、おそらくそれほど多くはないでしょう。一方、500年前にさかのぼれば、創造的なことをしている人たちがたくさんいたはずです。それが彼らの言い分なのです。
Lex Fridman 3:05:45
今日、あなたは計算について考え、謙虚な気持ちになったわけですが、人生の意味とは何だと思いますか?
Stephen Wolfram 3:05:55
私の態度は、自分がすることで充実感を得られることをする、というものですが、必ずしも自分のすることすべてを、より広い文脈に基づいて正当化できるかどうかはわかりません。つまり、私にとって、自分が充実していると感じることは、たまたま、大きなものもあれば、もっと小さなものもあるのだと思います。
例えば、教育や人に何かを教えることなどに興味を持つようになりましたが、これは若い頃にはそれほど興味がなかったことです。そして、それを世界的な意味で正当化することができるでしょうか?世界的に重要だと思う理由を説明することはできますが、私がそれをする局所的な理由は、個人的に充実しているからだと思います。
これは、AI倫理のような議論では説明できません。私の人生の基本的な真実を見つけることはできないと思いますが、それ以上に、文明全体の倫理の基本的な真実を示唆することができるでしょうか?それは私の、私の、私の、それはそうでしょう、それはそうでしょう、それは一種の、私の考えです。
Lex Fridman 3:07:25
私はあなたの視点であり、あなたの地元であり、あなたはセルラー・オートマトンの一細胞に過ぎませんが、人生のさまざまな時期に、さまざまな種類の目標や構造などを持っていました。しかし、ある意味では、私の観察によると、宇宙は自分自身を理解するためにあなたを利用しているようで、あなたはそれに気付いていないのですね。
Stephen Wolfram 3:07:49
ええ、そうですね。もし、宇宙のすべてを何らかの単純なルールに還元することができれば、すべてはいわばつながっていることになります。だから、どうしようもないのです。
その場合、もし私がそのルールがどのように機能しているかの発見に関わっていれば、それは宇宙がそのように設定した不可抗力だということになりますね。しかし、私が少し気になっているのは、物理学の基礎理論を見つけるという目標は、例えば、もし本当に私たちが仮想化された意識のようなものになったとしたら、残念なことに、その設定では人々は物理学の基礎理論を今よりも気にしなくなるだろうということです。
仮想化された意識を想像すると、仮想化された意識は永遠に何をするのか?そうですね、宇宙をそのまま表現したビデオゲームを探索するか、あるいは、予約を解除して、あらゆる可能な宇宙のうちの計算の宇宙を探索し始めるかですね。そうですね。歴史の未来像では、体のない意識が、いわば永遠に私の新しい科学のようなものを追求しているようなもので、それが結局、人間の条件のようなものの未来を象徴するものです。
Lex Fridman 3:09:35
これ以上の終わり方はないと思いますよ。今日のお話はとても光栄です。本当にありがとうございました。素晴らしかったです。あなたはとてもよくやってくれました。Stephen Wolframとの会話をお聞きいただきありがとうございました。スポンサーのExpressVPNとcash appに感謝します。
expressvpn@expressvpn.com slash flex podとcash appをダウンロードしてポッドキャストのサポートをご検討ください。このポッドキャストをお楽しみいただけましたら、YouTubeのレビューやAppleのポッドキャストで購読したり、Patreonでサポートしたり、TwitterのLex Friedmanで私とつながってください。
それでは、Stephen Wolframの言葉をご紹介します。私たち人間が、実質的には、非常に単純なルールを持つセルラー・オートマタと変わらない計算能力を持っていることを知って、少し謙虚になったかもしれません。しかし、計算等価性の原則は、究極的には私たちの宇宙全体にも同じことが言えることを示唆しています。
科学の世界では、私たち人間は宇宙に比べて取るに足らない存在であるかのように思われがちですが、計算量等価性の原理は、ある意味で私たち人間も同じレベルにあることを示しています。お聴きいただきありがとうございました。また次回お会いしましょう。

