Contents
writings.stephenwolfram.com/2023/02/what-is-chatgpt-doing-and-why-does-it-work/
それは、ただ一言ずつ言葉を足していくこと
ChatGPTは、表面的には人間が書いたような文章を自動生成することができるのが特徴で、予想外だった。しかし、どのようにそれを行うのだろうか?また、なぜうまくいくのだろうか?ここでは、ChatGPTの内部で起こっていることを大まかに説明し、なぜ意味のあるテキストを生成することができるのかを探ってみたいと思う。最初に断っておきますが、私は何が起こっているかという全体像に焦点を当てるつもりである。(また、これから述べることの本質は、ChatGPTと同様に、現在の他の「大規模言語モデル」[LLM]にも当てはまる)。
まず最初に説明しておくと、ChatGPTが基本的に常にやろうとしていることは、これまでに得たどんな文章でも「妥当な続き」を作ることである。ここで「妥当」というのは、「何十億ものウェブページで人々が書いたものを見て、誰かが書くと予想されるもの」、という意味である。
例えば、「AIの最も優れた点は、その能力である」という文章があるとする。何十億ページもの人間が書いたテキスト(ウェブやデジタル化された書籍など)をスキャンして、このテキストのすべてのインスタンスを見つけ、次にどんな単語が来るかを何分の一の確率で見ることができると想像してほしい。ChatGPTは、文字通りのテキストを見るのではなく、ある意味で「意味が一致する」ものを探すということを除いては、事実上このようなことを行っている。しかし、最終的には、その後に続く可能性のある単語のリストを「確率」とともにランク付けして出力する。

そして、ChatGPTがエッセイを書くとき、本質的にやっていることは、「これまでの文章から、次の単語は何にするか」を何度も何度も尋ねて、そのたびに単語を追加している、ということである。(より正確には、これから説明するように、「トークン」を追加しているのだが、これは単語の一部である可能性もあり、そのため「新しい単語を作る」こともある)。
しかし、各ステップで、確率の高い単語のリストを得ることができる。しかし、実際にどの単語を選んでエッセイに追加すればいいのだろうか?それは、「最高ランク」の単語(つまり、最も高い「確率」が割り当てられた単語)であるべきだと考えるかもしれない。しかし、ここでちょっとしたブードゥー教が入り込み始めるのである。なぜかというと、いつか科学的に解明されるかもしれないが、常に最高ランクの単語を選ぶと、「創造性を発揮しない」(時には一字一句繰り返す)、非常に「平板な」作文ができあがる。しかし、時々(ランダムに)下位の単語を選ぶと、「より面白い」作文が出来上がる。
ここにランダム性があるということは、同じプロンプトを複数回使えば、毎回違うエッセイができあがる可能性が高いということである。また、ブードゥー教の考え方に沿って、下位の単語が使われる頻度を決める、いわゆる「温度」というパラメーターがあるのだが、エッセイ生成においては、「温度」は0.8が最適だと判明している。(ここで強調したいのは、「理論」ではなく、あくまで「実践」でわかったということである。また、例えば「温度」という概念があるのは、統計物理学でおなじみの指数分布がたまたま使われているからで、「物理的」なつながりはない(少なくとも私たちが知る限りは)。
その代わりに、よりシンプルなGPT-2システムを使うことにする。そのため、私がお見せするものはすべて、皆さんが自分のコンピュータですぐに実行できるようなWolfram Languageのコードを含んでいる。(画像をクリックすると、その背後にあるコードがコピーされる)
例えば、上の確率の表を取得する方法は以下の通りである。まず、基礎となる「言語モデル」ニューラルネットを取得する必要がある。

後ほど、このニューラルネットの内部を覗いて、その仕組みについて説明する。しかし今は、このブラックボックスとしての「ネットモデル」をこれまでのテキストに適用し、モデルが言う「続くべき確率の上位5語」を求めるだけでいいのである。

これは、その結果を、明示的にフォーマットされた「データセット」にするものである。

「モデルの適用」を繰り返し、各ステップで最も高い確率を持つ単語(このコードではモデルからの「決定」として指定)を追加していくとどうなるか。

もっと長く続けるとどうなるのだろう?この場合(「ゼロ温度」)、すぐに出てくるものは、むしろ混乱し、繰り返しになる。

しかし、常に「トップ」の単語を選ぶのではなく、時々「トップでない」単語をランダムに選ぶとしたらどうだろう(「ランダム性」は「温度」0.8に相当)。ここでもまた、テキストを積み上げることができる。

そして、この5つの例のように、毎回異なるランダムな選択がなされ、テキストも異なるものになるのである。

最初のステップでも、「次の言葉」の候補はたくさんあるのだが(温度0.8)、その確率はすぐに下がってしまう(そう、この対数プロットの直線は、言語の一般的な統計に非常に特徴的なn-1「べき乗」減衰に対応している)ことは指摘に値するだろう。

では、一方が長く続くとどうなるのか?ここにランダムな例がある。トップワード(温度ゼロ)の場合よりはましですが、それでもせいぜいちょっと変な感じである。

A1の最大の特徴は、パニックになったり無視したりするのではなく、周囲を見渡し、納得させることができる点です。これは、A1の “doing its job”、あるいはA1の “run-of-the-mill “と呼ばれているものです。確かに、無限のステップを踏んで、他のシステムと統合できる機械を開発したり、本当に機械である1つのシステムをコントロールすることは、A1の最も基本的なプロセスの1つである。人間と機械のインタラクションもさることながら、A1ではクリエイティビティも重要な要素でした。
これは、最もシンプルなGPT-2モデル(2019年製)で行った。より新しく、より大きなGPT-3モデルでは、結果はより良くなっている。同じ「プロンプト」で、一番大きなGPT-3モデルで作成したトップワード(気温ゼロ)のテキストがこちらである。

A1の最大の特長は、プロセスを自動化し、迅速かつ正確に意思決定を行うことができる点です。A1は、データ入力などの日常的な作業を自動化するだけでなく、顧客行動の予測や大規模なデータセットの分析など、複雑な意思決定にも利用することができます。また、お客様からの問い合わせに迅速かつ正確に対応することで、顧客サービスの向上にも活用できます。また、医療診断の精度向上や創薬プロセスの自動化にも活用できます。
そして、「温度0.8」でのランダムな例である。

A1の最大の特徴は、時間をかけて学習・成長し、継続的に性能を向上させ、より効率的な作業を可能にすることです。また、日常的な作業を自動化することで、人間はより重要な作業に集中することができます。また、A1は、人間には不可能な意思決定や洞察の提供にも利用することができます。
確率はどこから来るのか?
なるほど、ChatGPTは常に確率に基づいて次の単語を選んでいる。しかし、その確率はどこから来るのだろうか?もっと簡単な問題から始めよう。英文テキストを一文字ずつ生成することを考えよう。各文字の確率はどのように計算すればよいのだろうか?
例えば、Wikipediaの”cats “の記事の文字数をカウントする。例えば、Wikipediaの「cats」の記事中の文字を数えると、このようになる。

そして、これは「犬」にも同じことが言える。

結果は似ているが、同じではない(”o 「は」dogs “の冠詞でより一般的であることは間違いない、結局のところ、”dog “という単語自体に出現するからである)。それでも、十分に大きな英文のサンプルを取れば、いずれは少なくともかなり一貫した結果が得られると期待できる。

この確率で文字列を生成するだけで、どのようなものが得られるのか、そのサンプルを紹介する。
これをある確率で文字に見立ててスペースを入れることで、「言葉」に分解することができる。
「言葉の長さ」の分布を英語のそれと無理やり一致させることで、「言葉」の作り方を少し工夫することができるのである。
ここではたまたま「実際の言葉」は出てかなかったが、結果は少し良くなってきている。しかし、さらに前進するには、それぞれの文字を別々にランダムに選ぶ以上のことをする必要がある。例えば、「q」があれば、次の文字は基本的に「u」でなければならないことが分かっている。
ここで、文字単体の確率をプロットしてみる。

そして、典型的な英語のテキストにおける文字のペア(「2-gram」)の確率を示すプロットがこちらである。最初の文字がページ全体に、2番目の文字がページの下に表示されている。

そして、例えば、「q」の列は「u」の行を除いて空白(確率ゼロ)であることがわかる。では、「単語」を一文字ずつ生成するのではなく、この「2-gram」確率を使って、二文字ずつ見て生成してみよう。この結果には、いくつかの「実際の単語」が含まれている。
十分な量の英文テキストがあれば、1文字や2文字のペア(2-gram)の確率だけでなく、より長い文字列の確率についても、かなり良い推定値が得られる。そして、徐々に長いn-gramの確率を持つ「ランダムワード」を生成すると、徐々に「現実的」になっていくことがわかる。

しかし、ここでは、ChatGPTと同じように、文字ではなく単語全体を扱っていると仮定しよう。英語には、一般的によく使われる単語が4万語ほどある。そして、大規模な英文コーパス(例えば数百万冊、全部で数千億語)を見れば、それぞれの単語がどの程度一般的だろうか推定することができる。これを利用して、各単語がコーパスに出現する確率と同じ確率で独立にランダムに選ばれた「文」を生成し始めることができる。以下は、その例である。
驚くなかれ、これはナンセンスなのだ。では、どうすればよいのだろうか。文字の場合と同じように、単一の単語の確率だけでなく、単語のペアや長いn-gramの確率を考慮するようにすればいい。以下は、”cat “という単語から始まる5つのペアの確率の例である。

少しは「常識的な見た目」になっていたね。そして、十分に長いn-gramを使うことができれば、基本的に「ChatGPTが得られる」と想像するかもしれない。つまり、「正しい論文全体の確率」を持つ単語のエッセイの長さのシーケンスを生成するものが得られると。しかし、問題は、そのような確率を推論できるほど、これまでに書かれた英文がないことである。
Webをクロールすれば数千億語、電子化された書籍ならさらに数千億語が存在するかもしれない。しかし、一般的な単語が4万語あるとして、2-gramの可能性があるものだけでもすでに16億語、3-gramの可能性があるものだけでも60兆語あるのである。だから、世の中にあるテキストから、これらすべての確率を推定することはできないのである。さらに、20文字程度の「エッセイの断片」になると、可能性の数は宇宙の粒子の数よりも多くなり、ある意味、すべてを書き表すことはできない。
では、どうすればいいのだろうか。それは、今まで見てきたテキストのコーパスの中で、そのようなシーケンスを明示的に見たことがなくても、シーケンスが発生する確率を推定できるようなモデルを作ることである。ChatGPTの核となるのは、まさにその確率を推定するために構築された、いわゆる「大規模言語モデル」(LLM)なのである。
モデルとは?
例えば、ピサの塔の各階から落とした大砲の弾が地面に落ちるまでの時間を知りたいとする(1500年代後半にガリレオが行ったように)。まあ、それぞれのケースで測定して、結果の表を作ればいいのだが。あるいは、理論科学の本質である、それぞれのケースを測定して記憶するのではなく、答えを計算するためのある種の手順を与えるモデルを作ることもできる。
例えば、大砲の玉がいろいろな階から落ちてくるのにどれくらい時間がかかるかという(やや理想的な)データがあるとしよう。
 データがない階から落下するのにかかる時間は、どうすればわかるのだろうか。この場合、既知の物理法則を使って計算することができる。しかし、データしかなく、それを支配する基本法則がわからないとする。その場合、数学的な推測をすることになる。例えば、モデルとして直線を使うべきかもしれない。
データがない階から落下するのにかかる時間は、どうすればわかるのだろうか。この場合、既知の物理法則を使って計算することができる。しかし、データしかなく、それを支配する基本法則がわからないとする。その場合、数学的な推測をすることになる。例えば、モデルとして直線を使うべきかもしれない。

いろいろな直線を選ぶことができる。しかし、これは与えられたデータに平均的に最も近いものである。そして、この直線から、どの階でも落下するまでの時間を推定することができるのである。
なぜ、ここで直線を使おうと思ったのだろうか?それは、数学的に単純なことだからだ。数学的に単純なものであり、私たちが測定した多くのデータは数学的に単純なもので十分適合することが分かっている。もっと数学的に複雑なもの、たとえばa+bx+cx2を試してみると、この場合はもっとうまくいく。

でも、うまくいかないこともある。例えば、a+b/x+csin(x)でできる最善のことは以下の通りである。

「モデルレス・モデル」というものは存在しないことを理解しておく必要がある。どのようなモデルであっても、その根底には特定の構造があり、データに適合させるために「回すことのできるノブ」(すなわち設定できるパラメータ)のセットがある。ChatGPTの場合、そのような「ノブ」がたくさん使われており、実際には1750億個もある。
しかし、注目すべきは、ChatGPTの基本構造が、たったこれだけのパラメータで、次の単語の確率を計算するモデルとして十分であり、エッセイのような長さの文章を作成するのに十分であることである。
人間らしいタスクのためのモデル
先ほどの例では、単純な物理学に由来する数値データのモデルを作ったが、ここでは数世紀前から「単純な数学が適用される」ことが知られている。しかし、ChatGPTの場合は、人間の脳が生成するような人間の言語のテキストをモデル化しなければならない。そして、そのようなものには、(少なくともまだ)「簡単な数学」のようなものはない。では、そのモデルとはどのようなものだろうか?
言語について話す前に、もう一つの人間のようなタスクである画像認識について話しておこう。そして、その簡単な例として、数字の画像を考えてみよう(そう、これは典型的な機械学習の例である)。
 ひとつは、各桁のサンプル画像をたくさん用意することである。
ひとつは、各桁のサンプル画像をたくさん用意することである。
 それなら、入力された画像が特定の数字に対応しているかどうかを調べるには、手持ちのサンプルとピクセル単位で比較すればいいわけである。しかし、人間にはもっと優れた方法があるようだ。例えば、手書きで書かれた数字や、さまざまな変形や歪みがある数字でも認識することができるのだろうから。
それなら、入力された画像が特定の数字に対応しているかどうかを調べるには、手持ちのサンプルとピクセル単位で比較すればいいわけである。しかし、人間にはもっと優れた方法があるようだ。例えば、手書きで書かれた数字や、さまざまな変形や歪みがある数字でも認識することができるのだろうから。
 では、各画素のグレーレベル値を変数xiとしたとき、それらの変数を評価したときに、その画像が何桁目だろうかを示す関数はあるのだろうか?そのような関数を作ることは可能であることがわかった。しかし、驚くほど簡単ではない。典型的な例では、おそらく50万回の数学的演算が必要になるだろう。
では、各画素のグレーレベル値を変数xiとしたとき、それらの変数を評価したときに、その画像が何桁目だろうかを示す関数はあるのだろうか?そのような関数を作ることは可能であることがわかった。しかし、驚くほど簡単ではない。典型的な例では、おそらく50万回の数学的演算が必要になるだろう。
しかし、最終的には、画像の画素値の集まりをこの関数に入力すると、どの桁の画像かを示す数値が出力される。このような関数の作り方やニューラルネットの考え方は後ほど紹介する。ここでは、この関数をブラックボックスとして、例えば手書きの数字の画像を(画素値の配列として)入力すると、それに対応する数字が出てくるようにする。

しかし、実際にはどうなのだろうか。例えば、ある数字を徐々にぼかしていくとする。この関数は、しばらくの間はまだその数字を「2」と「認識」している。しかし、すぐに「わからなく」なり、「間違った」結果を出し始める。

しかし、なぜそれが「間違った」結果だと言うのだろうか?この場合、私たちは「2」をぼかすことですべての画像を手に入れたことを知っている。しかし、人間が画像を認識する際のモデルを作ることが目的なら、本当に問うべきは、どこから来たかわからないぼかし画像を1枚見せられたら、人間はどうしたかということである。
そして、この関数から得られる結果が、人間が言うであろうことと典型的に一致する場合、「良いモデル」であると言えるだろう。そして、自明ではない科学的事実として、このような画像認識タスクの場合、これを実現する関数を構築する方法が基本的に分かっている。
その効果を「数学的に証明」できるのか?いや、できない。なぜなら、それをするためには、私たち人間がやっていることを数学的に理論化する必要があるからだ。「2」の画像で、いくつかのピクセルを変えてみよう。たった数ピクセルの「ずれ」でも、その画像を「2」と見なすべきだと想像するかもしれない。しかし、それはどこまでが「2」なのだろうか。それは、人間の視覚の問題である。そして、その答えは間違いなく、ハチやタコでは異なるだろうし、宇宙人と思われる人たちでは全く異なる可能性がある。
ニューラルネット
では、画像認識のようなタスクの典型的なモデルは、実際にはどのように機能しているのだろうか?現在最も人気があり、成功しているのはニューラルネットを使う方法である。ニューラルネットは、1940年代に今日に近い形で発明されたもので、脳の働きを単純に理想化したものと考えることができる。
人間の脳には約1000億個のニューロン(神経細胞)があり、それぞれが1秒間に最大1000回の電気パルスを発生させることができる。ニューロンは複雑な網目状に結合しており、各ニューロンはツリー状に枝分かれして、他の何千ものニューロンに電気信号を伝達することができる。大まかには、あるニューロンがある瞬間に電気パルスを発生させるかどうかは、他のニューロンからどのようなパルスを受け取ったかに依存し、異なる接続は異なる「重み」をもって貢献する。
私たちが「映像を見る」とき、映像の光子が目の奥にある「視細胞」に落ちると、神経細胞に電気信号が発生する。この神経細胞は他の神経細胞とつながり、最終的に信号が何層もの神経細胞を通過する。そして、この過程で私たちは画像を「認識」し、最終的に「2を見ている」という「思考を形成」します(最終的には「2」という言葉を声に出して言うようなこともあるかもしれないね)。
前節の「ブラックボックス」関数は、このようなニューラルネットの「数学化」バージョンである。たまたま11層(ただし「コア層」は4層だけ)ある。

このニューラルネットには、特に「理論的な導き」があるわけではなく、1998年当時、工学的に構築され、動作が確認されたものに過ぎないのである。(もちろん、これは私たちの脳が生物学的進化の過程で作られたと説明するのと大差はない)
さて、ではこのようなニューラルネットは、どのようにして「物事を認識」するのだろうか?その鍵は「アトラクター」という概念にある。手書きの「1」と「2」の絵があるとしよう。

1の画像はすべて「ある場所に引き寄せられたい」し、2の画像はすべて「別の場所に引き寄せられたい」のである。あるいは、「2」より「1」に近いイメージは「1」に、その逆は「2」に寄ってほしい。
わかりやすい例として、平面上に点で示されたある位置があるとする(現実の設定では、それはコーヒーショップの位置かもしれない)。すると、平面上のどの点から出発しても、必ず一番近い点にたどり着きたいと思う(つまり、必ず一番近い喫茶店に行く)のではないだろうか。これを表すには、平面を理想的な「流域」で区切られた領域(「アトラクタベースン」)に分割すればよい。

これは一種の「認識タスク」であり、与えられた画像がどの数字に「最も似ているか」を識別するようなことはせず、与えられた点がどの点に最も近いかを、極めて直接的に見ていると考えることができる。(ここで紹介する「ボロノイ図」は、2次元ユークリッド空間の点を分離するものである。数字認識タスクは、これとよく似たことを、各画像の全画素のグレーレベルからなる784次元空間で行っていると考えることができる)。
では、ニューラルネットに「認識タスクをさせる」ためにはどうすればよいのだろうか。非常に単純なケースを考えてみよう。

位置{x,y}に対応する「入力」を受け取り、それが3つの点のうちどれに最も近いかを「認識」することが目的である。言い換えれば、{x,y}の関数を計算させるということである。

では、ニューラルネットでどのようにこれを実現するのだろうか。最終的にニューラルネットは理想化された「ニューロン」の接続された集合体である。- 通常は層状に配置されている。- 簡単な例を挙げよう。

それぞれの「ニューロン」は、単純な数値関数を評価するように設定されている。そして、ネットワークを「使う」ためには、単純に数字(座標xやyなど)を一番上に送り込み、各層のニューロンに「関数を評価」させ、その結果をネットワークを通して先に送り込み、最終的に一番下で最終結果を出すのである。

従来の(生物学的な)設定では、各ニューロンには、前の層のニューロンから「入ってくる接続」のセットが効果的にあり、それぞれの接続には一定の「重み」(これは正または負の数である)が割り当てられている。あるニューロンの値は、「前のニューロン」の値に対応する重みを掛け、それらを合計して定数を掛け、最後に「閾値」(または「活性化」)関数を適用することによって決定される。数学用語で言えば、あるニューロンが入力x={x1,x2…}を持つ場合、f[w.x+b]を計算する。ここで重みwと定数bは、一般にネットワーク内のニューロンごとに異なって選ばれるが、関数fは通常同じものである。
w.x+bを計算するのは、単に行列の乗算と加算の問題である。「活性化関数」fは非線形性を導入する(そして最終的には非自明な挙動をもたらす)。一般にさまざまな活性化関数が用いられるが、ここではRamp(またはReLU)だけを用いることにする。

ニューラルネットに実行させたいタスクごとに(あるいは同様に、評価させたい機能全体ごとに)、異なる重みが選択されることになる。(後述するが、これらの重みは通常、求める出力の例から機械学習を用いてニューラルネットを「訓練」することで決定される)。
結局のところ、すべてのニューラルネットは、書き出すと面倒かもしれないが、ある全体的な数学関数に対応しているだけなのである。上の例では、次のようになる。

ChatGPTのニューラルネットも、このような数学の関数に相当するだけで、実質的には何十億もの項を持つことになる。
しかし、個々のニューロンの話に戻ろう。ここでは、2つの入力(座標xとy)を持つニューロンが、様々な重みと定数(および活性化関数としてのRamp)を選択した場合に計算できる関数の例をいくつか示す。

しかし、上から見た大きなネットワークはどうだろうか?さて、その計算結果はこうだ。

これは「正しい」とは言えないが、上で紹介した「最近接点」関数に近いものである。
他のニューラルネットで何が起こるか見てみよう。いずれの場合も後で説明するように、機械学習を使って最適な重みの選択を見つけるのである。そしてその重みを持つニューラルネットが計算するものをここに示す。

一般に大きなネットワークは、目指す関数をよりよく近似してくれる。また、「各アトラクターベイスンの中央部」では、通常、思い通りの答えが得られる。しかし境界では、ニューラルネットが「なかなか決心できない」ため、事態はより混乱する。
このような単純な数学的な「認識課題」であれば、「正解」は明確である。しかし、手書きの数字を認識する問題では、そうもいかない。もし誰かが「2」と書いたら、「7」に見えてしまう、などということはないだろうか。それでも、ニューラルネットがどのように数字を識別しているのかを問うことはできる。

ネットワークがどのように区別しているのか、「数学的に」説明できるのだろうか?そうではない。ニューラルネットがすることをやっているだけ」なのである。しかし、それは通常、私たち人間が行う区別とかなりよく一致するようであることがわかる。
もう少し凝った例を挙げてみよう。猫と犬の画像があるとする。そして、それらを区別するように訓練されたニューラルネットがあるとする。このニューラルネットが、いくつかの例でどのような働きをするか見てみよう。

今となっては、何が「正解」なのか、さらにわからなくなった。キャットスーツを着た犬はどうなんだろう?などなど。ニューラルネットは与えられた入力が何であれ、答えを生成する。そして、人間がやりそうなことと合理的に一致する方法で、それを行うことが判明した。前述したように、これは「第一原理から導き出される」事実ではない。少なくともある領域では、経験的にそうであることが分かっているに過ぎないのである。しかし、これはニューラルネットが有用である重要な理由である。ニューラルネットは何らかの形で「人間らしい」物事の進め方を捉えるからだ。
自分に猫の写真を見せて、「なぜそれが猫なのだろうか?」たぶん、「そうだね、耳がとがっているね、など」と言い始めると思う。でも、その画像をどうやって猫だと認識したのか、説明するのはあまり簡単ではない。ただ、あなたの脳がそれを理解したというだけだ。しかし、脳の場合、その中に入って、どうやってそれを理解したかを見る方法は(少なくとも今のところ)ない。では、ニューラルネットの場合はどうだろう。猫の絵を見せれば、それぞれの「ニューロン」が何をするかは一目瞭然だ。しかし、基本的な可視化を行うことさえ、通常は非常に困難である。
上記の「最近接点」問題で使用した最終的なネットでは17個のニューロンがある。手書きの数字を認識するためのネットでは2190個。そして、猫と犬を認識するためのネットでは、60,650個ある。通常であれば、60,650次元の空間を可視化するのはかなり難しいだろう。しかし、これは画像を扱うためのネットワークなので、ニューロンの多くの層は、見ているピクセルの配列のように、配列に組織化されている。
また、典型的な猫の画像を例にとると

その多くは、「背景のない猫」や「猫の輪郭」など、私たちが容易に解釈できるものである。

10層目になると、何が起こっているのか解釈するのが難しくなる。

しかし、一般的には、ニューラルネットは「ある特徴」(とんがり耳もその一つかもしれない)を選び出し、それを使って、その画像が何だろうかを決定していると言えるかもしれない。しかし、その特徴は「とんがり耳」のように名前がついているものなのだろうか?ほとんどの場合、そうではない。
私たちの脳は、同じような機能を使っているのだろうか?ほとんどの場合、それはわからない。しかし、ここで紹介するようなニューラルネットの最初の数層は、脳の視覚処理の第一階層で選択されるものと類似していると思われる画像の側面(物体のエッジなど)を選択するようであることは注目すべきことである。
しかし、ニューラルネットで「猫認識の理論」を求めるとしよう。こう言うことができる。「この特殊なネットではそれができる」と言えば、それが「どれほど難しい問題か」(例えば、何ニューロンや何層が必要なのか)をすぐに理解することができる。しかし、少なくとも今のところ、ネットワークが何をしているのかを「物語的に説明する」方法は持っていない。それは、ネットワークが本当に計算不可能であり、各ステップを明示的にトレースする以外に、何を行っているかを見つける一般的な方法がないからかもしれない。あるいは、私たちが「科学を解明」しておらず、何が起こっているかを要約できるような「自然法則」を特定できていないだけなのかもしれない。
ChatGPTによる言語生成の話でも、同じような問題に遭遇することになる。そしてまた、「やっていることを要約する」方法があるかどうかは、明らかではない。しかし、言語の豊かさと詳細さ(そして私たちの経験)により、画像の場合よりもさらに前進することができるかもしれない。
機械学習、そしてニューラルネットのトレーニング
ここまでは、特定のタスクのやり方を「すでに知っている」ニューラルネットについて話してきた。しかし、ニューラルネットが(おそらく脳においても)非常に有用なのは、原理的にあらゆる種類のタスクをこなせるだけでなく、それらのタスクをこなすために「例から学習」させることができる点である。
猫と犬を見分けるニューラルネットを作る場合、例えばヒゲを明示的に見つけるようなプログラムを書く必要はなく、「これは猫、これは犬」という例をたくさん見せて、そこから見分け方を「機械学習」させるだけでよいのである。
そしてポイントは、学習したネットワークが、見せられた特定の例から「汎化」することである。このように、見せられた猫画像の特定の画素パターンを認識するのではなく、「一般的な猫らしさ」を基準にして、ニューラルネットワークが画像を識別することができるのである。
では、実際にニューラルネットの学習はどのように行われるのだろうか。基本的に私たちが常に心がけているのは、与えた例をニューラルネットがうまく再現できるような重みを見つけることである。そして、これらの例の「間」を「合理的」に「補間」(あるいは「汎化」)することをニューラルネットに期待するのである。
上の最近接点の問題よりもさらに単純な問題を見てみよう。ニューラルネットに関数を学習させるだけにしてみよう。

この作業には、次のような入力と出力が1つずつしかないネットワークが必要である。

しかし、どのような重みなどを使えばいいのだろうか?ニューラルネットは可能な限りの重みを使って、何らかの関数を計算する。例えば、ランダムに選んだいくつかの重みを使って、次のような計算をする。

そして、そう、いずれの場合も、私たちが求める関数の再現にはほど遠いことが、はっきりとわかるのである。では、どうすれば関数を再現する重みが見つかるのだろうか。
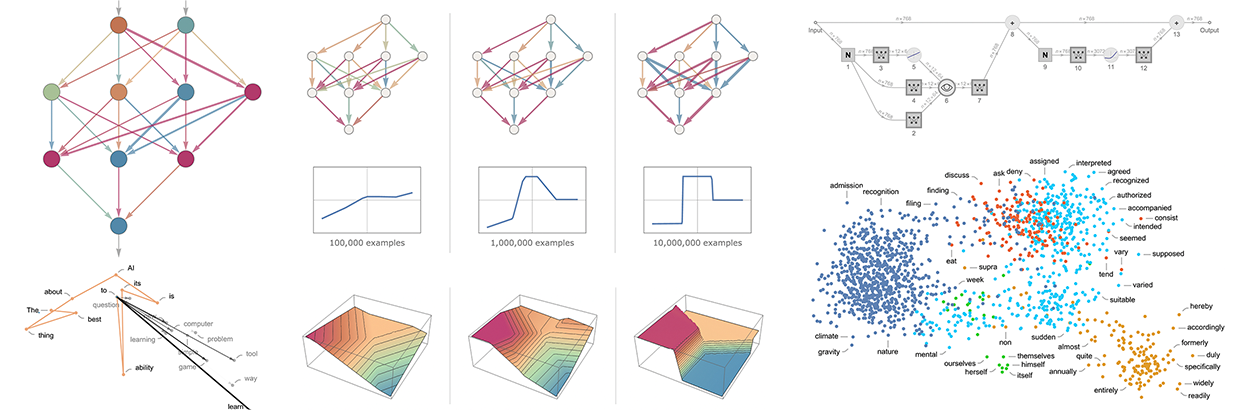
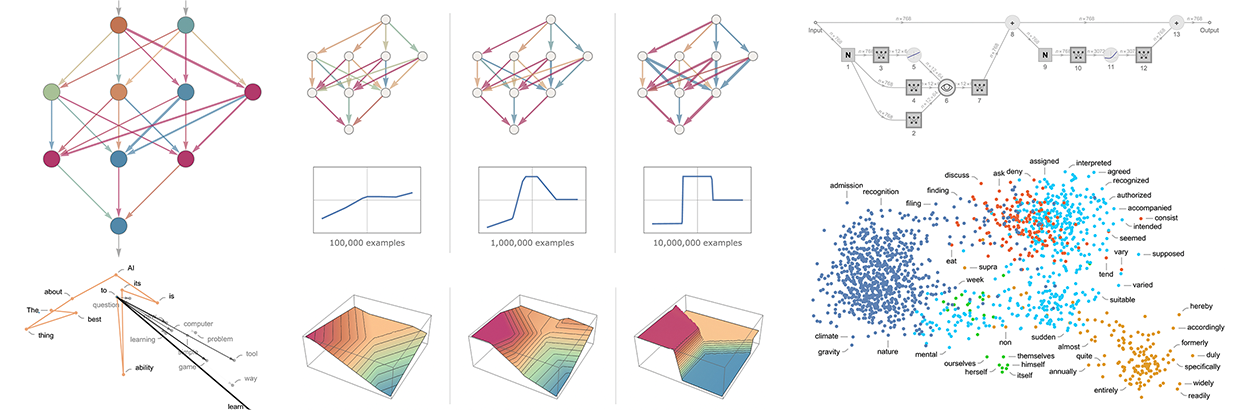
基本的な考え方は、「入力→出力」の例をたくさん用意して「そこから学習」し、その例を再現するような重みを探そうというものである。徐々に例を増やしていった結果がこちらである。

この「学習」の各段階で、ネットワークの重みを徐々に調整していくと、最終的には目的の機能をうまく再現するネットワークができあがることがわかる。では、どのように重みを調整するのか。基本的な考え方は、各ステージにおいて、欲しい機能が得られるまでの「距離」を確認し、それに近づくように重みを更新していくことである。
「どの程度離れているか」を知るために、通常「損失関数」(あるいは「コスト関数」)と呼ばれるものを計算する。ここでは単純な(L2)損失関数を使い、得られた値と真の値との差の二乗の総和を計算する。そして、学習が進むにつれて、損失関数は徐々に減少し(タスクごとに異なる「学習曲線」に沿って)、ネットワークが(少なくとも近似的に)望む関数をうまく再現するポイントに到達することがわかる。

さて、最後に重要なのは、損失関数を小さくするために重みを調整する方法である。先ほどから言っているように、損失関数は、得られた値と真の値との「距離」を示している。しかし、「今ある値」は、現在のニューラルネットのバージョンと、その中の重みによって、各段階で決定される。しかし、ここで重みが変数、例えばwiであったとしよう。この変数の値をどのように調整すれば、変数に依存する損失を最小化できるかを知りたいのである。
例えば、(実際に使われる典型的なニューラルネットを驚くほど単純化して)2つの重みw1とw2だけがあるとする。すると、w1とw2の関数として、次のような損失が考えられる。

数値解析はこのような場合の最小値を求めるための様々なテクニックを提供する。しかし、典型的な方法は、以前のw1,w2が何であれ、最急降下の経路を漸進的にたどることである。

山を流れる水のように、この手順で保証されるのは、表面の局所的な最小値(「山中湖」)に行き着くことだけで、究極のグローバルミニマムには到達しない可能性があるのだ。
「重さの風景」上で最急降下の経路を見つけることが実現可能であることは自明ではないだろう。しかし、微積分が助けになる。先に述べたように、ニューラルネットは常に入力とその重みに依存する数学的関数を計算していると考えることができる。しかし今度は、これらの重みに関して微分することを考えてみよう。微積分の連鎖法則は、事実上、ニューラルネットの連続する層で行われる演算を「解く」ことができることがわかった。その結果、少なくとも局所的な近似では、ニューラルネットの演算を「反転」させ、出力に関連する損失を最小化する重みを徐々に見つけることができる。
上の図は、重みが2つだけという非現実的で単純なケースで必要な最小化の方法を示している。しかし、もっと多くの重みがあっても(ChatGPTは1750億個を使用)、少なくともある程度の近似は可能であることが判明した。実際、2011年頃に起こった「ディープラーニング」の大きなブレークスルーは、ある意味で、重みが少ない場合よりも多い場合の方が、最小化を(少なくとも近似的に)行うのが簡単だという発見と関連していたのである。
つまり、直感に反して、ニューラルネットを使うと、単純な問題よりも複雑な問題の方が解きやすくなることがあるのである。その大まかな理由は、「重み変数」が多いと、高次元空間で「いろいろな方向から」最小値にたどり着けるのに対し、変数が少ないと、「出る方向」のない局所最小値(「山中湖」)にはまりやすくなるからだと思われる。
一般的なケースでは、ほぼ同じ性能を持つニューラルネットを実現するために、多くの異なる重みのコレクションが存在することを指摘しておく必要がある。また、実際のニューラルネットのトレーニングでは、多くのランダムな選択が行われ、このような「異なるが等価な解」を導くことがある。

しかし、そのような「別解」はそれぞれ、少なくともわずかに異なる振る舞いをする。また、例えば学習例を与えた領域の外側に「外挿」を求めると、劇的に異なる結果が得られることもある。

でも、どれが「正しい」のだろうか?というと、実はそうとも言い切れない。どれも「観測されたデータと一致している」のである。しかし、それらはすべて、「箱の外」で何をすべきかを「考える」ための異なる「生得的」な方法に対応している。そして、あるものは、私たち人間にとって、他のものよりも「より合理的」に見えるかもしれない。
ニューラルネット・トレーニングの実践と伝承
特にこの10年間は、ニューラルネットをトレーニングする技術に多くの進歩があった。そして、そう、基本的には芸術なのである。時には、特に後から振り返ってみると、少なくとも「科学的な説明」の片鱗が見えてくることもある。しかし、たいていの場合は試行錯誤の末に発見され、アイデアやトリックが追加されて、ニューラルネットの扱い方に関する重要な伝承が徐々に構築されていた。
いくつかの重要な部分がある。まず、特定のタスクにどのようなニューラルネットを使うべきかという問題がある。そして、ニューラルネットを学習させるためのデータをどのように入手するかという重要な問題がある。新しいニューラルネットは、すでに訓練された別のニューラルネットを直接組み込むか、少なくともそのニューラルネットを使って自分用の訓練例をより多く生成することができる。
ある人は、特定の種類のタスクごとに、異なるアーキテクチャのニューラルネットが必要だと考えたかもしれない。しかし、明らかに全く異なるタスクであっても、同じアーキテクチャが機能する場合が多いことが分かっている。このことは、あるレベルでは普遍的計算の考え(および私の計算等価性の原理)を思い起こさせるが、後で述べるように、これはむしろ、私たちが一般的にニューラルネットにやらせようとしているタスクが「人間に似た」もので、ニューラルネットが極めて一般的な「人間に似たプロセス」を捉えることができるという事実の反映であると考えている。
ニューラルネットの初期には、「ニューラルネットにはできるだけ何もさせるな」という考え方がありがちだった。例えば、音声をテキストに変換する場合、まず音声を解析し、音素に分割するなどの作業を行うべきだと考えられていた。しかし、少なくとも「人間に近いタスク」については、ニューラルネットに「エンド・ツー・エンドの問題」を学習させ、必要な中間特徴やエンコーディングなどを自ら「発見」させる方が良いということがわかった。
エンド・ツー・エンドの問題(End-to-End problem)とは、システムの全体的な性能を評価するときに、システム内のある部分だけでなく、全体としての性能を考慮する必要があるという問題である。特に、複数の機械学習やデータ処理のステップを含むシステムにおいて、それぞれのステップが良好に機能しても、システム全体のパフォーマンスが低い場合がある。
たとえば、音声認識システムにおいて、言語モデル、音響モデル、および音声処理アルゴリズムがある場合、それぞれのステップが最適であっても、システムの最終的な認識精度が低い可能性がある。この問題を解決するために、エンド・ツー・エンドのアプローチでは、システムの全体的なパフォーマンスを直接最適化することを目指する。つまり、入力から出力までのプロセスを単一のモデルで表現し、学習することで、より高い精度を実現することができる。
エンド・ツー・エンドのアプローチは、特に深層学習の発展によって重要性が高まっている。深層学習は、エンド・ツー・エンドのモデルを構築するための強力なツールであり、特に画像認識、音声認識、自然言語処理などのタスクにおいて良好な結果を出している。
また、ニューラルネットに複雑な個々のコンポーネントを導入して、実質的に「特定のアルゴリズムのアイデアを明示的に実装」させるという考え方もあった。その代わり、非常に単純な構成要素を扱い、(通常は理解できない方法でではあるが)「自分自身を組織化」させて、(おそらく)そのアルゴリズム的アイデアに相当するものを実現させる方がよいということが、今回もほとんど判明している。
とはいえ、ニューラルネットに関連する「構造化のアイデア」がないわけではない。例えば、局所的な接続を持つニューロンの2次元アレイは、少なくとも画像処理の初期段階においては非常に有用であると思われる。また、後述するように、ChatGPTなど、人間の言語を扱う際にも、「系列で振り返る」ことに重点を置いた接続パターンが有効であると思われる。
しかし、ニューラルネットの重要な特徴は、一般的なコンピュータと同様に、最終的にはデータを扱っているということである。そして、現在のニューラルネットは、ニューラルネットのトレーニングのアプローチとともに、数字の配列を扱うことに特化している。しかし、その配列は処理の過程で完全に並べ替えられ、形を変えることができるのである。例えば、先ほどの数字識別のためのネットワークは、2Dの「画像のような」配列から始まり、すぐに多くのチャンネルに「太く」なるが、その後、1Dの配列に「集中」し、最終的にさまざまな出力数字を表す要素が含まれるようになるのである。

しかし、では、あるタスクに必要なニューラルネットの大きさをどうやって判断すればいいのだろう?それは一種の芸術だ。あるレベルでは、「そのタスクがどのくらい難しいか」を知ることが重要である。しかし、人間のようなタスクの場合、それを推定するのは一般的に非常に困難である。確かに、コンピュータで非常に「機械的に」タスクをこなす体系的な方法はあるかもしれない。しかし、少なくとも「人間のようなレベル」でその作業を非常に簡単に行うことができるような、トリックやショートカットと思われるものがあるかどうかを知ることは困難である。あるゲームを「機械的に」プレイするには、巨大なゲームツリーを列挙する必要があるかもしれないが、「人間レベルのプレイ」を実現するには、もっと簡単な(「発見的」な)方法があるかもしれないのである。
小さなニューラルネットと簡単なタスクを扱っていると、「ここから先は無理だ」とはっきり分かることがある。例えば、前節のタスクで、いくつかの小さなニューラルネットを使った場合のベストは次のとおりである。

その結果、網が小さすぎる場合は、求める機能を再現できないことがわかった。しかし、ある大きさ以上であれば、少なくとも十分な時間をかけて、十分な例で訓練すれば問題ない。ところで、この写真はニューラルネットの言い伝えの1つである、より小さなネットワークでも、中間により少ない数のニューロンを通過させる「スクイーズ」があれば、回避できることが多いということを説明している。「(中間層なし」、いわゆる「パーセプトロン」ネットワークは基本的に線形関数しか学習できないが、中間層が1層でもあれば、少なくとも十分なニューロンがあれば、原理的にはいつでも任意の関数をうまく近似することが可能である、ということも述べておきたい)
さて、あるニューラルネットのアーキテクチャが決まったとする。ここで、ネットワークを学習させるためのデータを入手することが問題となる。ニューラルネットや機械学習全般に関する現実的な課題の多くは、必要な学習データの取得や準備に集中している。多くの場合(「教師あり学習」)、入力とそこから期待される出力の明示的な例を得たいと考える。例えば、画像に何が写っているかなどの属性でタグ付けしたい。このような場合、通常は多大な労力を費やして、タグ付けを行わなければならないだろう。しかし、すでに行われていることにおんぶに抱っこしたり、ある種の代理として利用したりできることが非常に多い。たとえば、ウェブ上の画像に付与されているaltタグを利用することができる。また、別の分野では、ビデオ用に作成されたクローズドキャプションを使用することもできる。また、言語翻訳のトレーニングのために、異なる言語で存在するウェブページや他のドキュメントのパラレルバージョンを使用することもできる。
ニューラルネットを特定のタスクのために訓練するには、どれくらいのデータを見せる必要があるのだろうか?これもまた、第一原理から推定するのは難しい。確かに、すでに別のネットワークで学習した重要な特徴のリストなどを「転送学習」することで、必要なデータを劇的に減らすことは可能である。しかし、一般にニューラルネットは、うまく学習するために「多くの例を見る」必要がある。そして、少なくともいくつかのタスクでは、例題が驚くほど反復的であることが、ニューラルネットの重要な伝承となっている。実際、ニューラルネットに手持ちのすべての例を何度も何度も見せることは、標準的な戦略である。これらの「トレーニングラウンド」(または「エポック」)のそれぞれで、ニューラルネットは少なくともわずかに異なる状態になり、特定の例を「思い出させる」ことが、「その例を記憶」させるために何らかの形で有効である。(そして、そう、これは人間の暗記における繰り返しの有用性と類似しているのかもしれない)。
しかし、同じ例を何度も繰り返すだけでは十分でないことも多い。その例のニューラルネットのバリエーションを示すことも必要だ。そして、その「データ拡張」のバリエーションが高度でなくても有用であることがニューラルネットの特徴である。基本的な画像処理で画像を少し修正するだけで、基本的にニューラルネットのトレーニングに「新品同様」にすることができるのである。同様に、自動運転車の訓練に使う実際の映像などが足りなくなったら、リアルワールドのシーンのようなディテールを持たないモデルビデオゲームのような環境でシミュレーションを行い、データを取得するだけでもいいのである。
ChatGPTのようなものはどうだろうか?教師なし学習ができるので、学習するためのサンプルを簡単に得ることができる。ChatGPTの基本的なタスクは、与えられたテキストをどのように継続させるかを考えることである。つまり、「学習用サンプル」を得るためには、テキストの一部を取得し、その末尾をマスクして、これを「学習用の入力」として使用すればよいのである。後ほど詳しく説明するが、要は、画像学習などと違って「明示的なタグ付け」が不要で、ChatGPTは与えられたテキストの例から直接学習すればいいのである。
では、ニューラルネットの実際の学習過程はどうなっているのだろうか?結局のところ、与えられた学習例をどのような重みでとらえるのが最適かを決定することになる。そして、その方法を微調整するために、あらゆる種類の詳細な選択と「ハイパーパラメータ設定」(重みを「パラメータ」と考えることができるため、このように呼ばれている)がある。損失関数にもさまざまな選択肢がある(二乗和、絶対値和など)。損失最小化の方法もさまざまである(各ステップで重み空間のどこまで移動するか、など)。さらに、最小化しようとする損失を連続的に推定するために、どの程度の大きさの「バッチ」例を表示するかといった問題がある。そして、機械学習(例えばWolfram Languageで行っているように)を応用して機械学習を自動化し、ハイパーパラメータのようなものを自動的に設定することができる。
しかし、最終的には、損失が徐々に減少していく様子を見ることで、トレーニングのプロセス全体を特徴づけることができる(この小さなトレーニングのWolfram Languageプログレスモニターのように)。

そして、一般的に見られるのは、損失はしばらく減少するが、最終的にはある一定の値で平坦になることである。この値が十分に小さければ、学習は成功したと言える。そうでなければ、ネットワークアーキテクチャを変えてみるべきというサインだろう。
学習曲線」が平坦になるまでの時間を知ることはできるのだろうか?他の多くのものと同様、ニューラルネットのサイズと使用するデータ量に依存して、近似的なべき乗のスケーリング関係があるように思われる。しかし、一般的な結論としては、ニューラルネットの学習は難しく、計算負荷がかかるということである。そして現実問題として、その労力の大半は、GPUが得意とする数値の配列に対する演算に費やされる。そのため、ニューラルネットのトレーニングは通常GPUの可用性によって制限されている。
将来、ニューラルネットを訓練する、あるいはニューラルネットが行うことを全般的に行う、根本的に優れた方法が現れるだろうか。ほぼ間違いなく、そうなると思う。ニューラルネットの基本的な考え方は、多数の単純な(基本的に同一の)コンポーネントから柔軟な「コンピューティング・ファブリック」を作り、この「ファブリック」を例から学習するように漸進的に変更できるようにすることである。現在のニューラルネットでは、この漸進的な変更を行うために、実数に適用される微積分の考え方を本質的に利用している。しかし、高精度な数値が必要なわけではなく、現在の手法でも8ビット以下で十分なことが分かってきている。
セルオートマトンのように、基本的に個々のビットに対して並列に動作する計算システムでは、このような漸進的な変更を行う方法はこれまで明らかにされていなかったが、それが不可能であると考える理由はない。実際、「2012年のディープラーニングのブレークスルー」のように、このような漸進的な修正は、単純なケースよりも複雑なケースの方が効果的かもしれない。
ニューラルネットは、おそらく脳に似ていて、ニューロンのネットワークは基本的に固定されており、ニューロン間の接続の強さ(「重み」)を変更するように設定されている。(少なくとも若い脳では、相当数のまったく新しい結合が成長することもあるのだろう)。しかし、これは生物学にとっては都合のよい設定かもしれないが、私たちが必要とする機能を実現するための最良の方法に近いかどうかは、まったくわからない。物理学プロジェクトを彷彿とさせるような、漸進的なネットワークの書き換えを伴うものの方が、最終的には良いのかもしれない。
ニューラルネットの学習は、基本的に逐次的に行われ、各バッチの例の影響が伝搬されて重みが更新される。そして実際、現在のコンピュータハードウェア(GPUを考慮しても)では、ニューラルネットの大部分は訓練中ほとんどの時間「アイドル」状態であり、一度に1つの部分のみが更新される。これはある意味、現在のコンピュータが、CPU(あるいはGPU)とは別にメモリを搭載している傾向があるからだ。しかし、脳ではそうではなく、ニューロンという「記憶素子」が、潜在的に「演算素子」でもあるのだと思われる。もし、未来のコンピュータのハードウェアをこのように構成することができれば、より効率的にトレーニングを行うことができるようになるかもしれない。
「きっと、大きなネットワークがあれば何でもできる!」
ChatGPTのような能力はとても素晴らしいので、「どんどん」大きなニューラルネットワークを訓練していけば、いずれは「何でもできる」ようになるのではないかと想像してしまう。そして、人間の思考にすぐにアクセスできるものに限って言えば、そうなる可能性は十分にある。しかし、過去数百年の科学の教訓は、形式的なプロセスで解明できることでも、人間の思考では容易に理解できないことがあるということだ。
自明でない数学は一つの大きな例である。しかし、一般的なケースは本当に計算なのだ。そして、最終的に問題となるのは、「計算の還元性」という現象である。計算の中には、何段階もかかると思われるようなものでも、実はすぐに「還元」できるものがある。しかし、計算不可逆性の発見は、それが必ずしもうまくいかないことを示唆している。そして、その代わりに、おそらく以下のようなプロセスがあり、そこで何が起こるかを解明するためには、本質的に各計算ステップをトレースする必要がある。

私たちが普段、脳で行っていることは、計算不可能性を回避するために特別に選ばれたものだと思われる。脳で計算をするには、特別な努力が必要だ。また、非自明なプログラムの動作ステップを自分の脳の中だけで「考え抜く」ことは、実際にはほとんど不可能である。
でも、そのためにはもちろんコンピュータがある。コンピュータを使えば、計算不可能な長いものも簡単にできるようになる。そして重要なのは、一般に、これには近道がないということである。
そう、ある特定の計算システムで起こる具体的な例をたくさん記憶することができるのだ。そして、少しは一般化できるような(「計算機的に還元可能な」)パターンを見ることもできるかもしれない。しかし、重要なのは、計算機的還元不能性とは、予期せぬことが起こらないという保証は決してできないということだ。
そして、最終的には、学習可能性と計算不可能性との間に、根本的な緊張関係が生まれる。学習には、規則性を利用してデータを圧縮する効果がある。しかし、計算機的不可逆性とは、最終的に規則性には限界があることを意味する。
実際問題として、セル・オートマトンやチューリング・マシンのような小さな計算装置を、ニューラルネットのような学習可能なシステムに組み込むことは想像できる。そして、そのような装置は、Wolfram|AlphaがChatGPTの良い道具であるように、ニューラルネットの良い「道具」として機能することができる。しかし、計算機的還元不能性は、そのようなデバイスの中に入って学習させることは期待できないことを意味している。
別の言い方をすれば、能力と訓練可能性の間には究極のトレードオフがある。計算能力を「真に利用」しようと思えば思うほど、システムは計算不可能性を示すようになり、訓練可能性が低くなる。そして、基本的に訓練可能であればあるほど、高度な計算を行うことができなくなる。
(なぜなら、各トークンの出力を生成するためのニューラルネットは、ループのない純粋な「フィードフォワード」ネットワークであり、自明ではない「コントロールフロー」を伴ういかなる種類の計算もできないからだ)。
もちろん、「既約計算ができることが本当に重要なのか」と思う人もいるかもしれない。実際、人類の歴史の大半において、それは特に重要なことではなかった。しかし、現代の技術世界は、少なくとも数学的計算を利用する工学の上に成り立っており、最近ではより一般的な計算も利用されるようになっている。そして、自然界を見ると、そこには再現不可能な計算がたくさんあり、それを模倣して技術的な目的に利用する方法が徐々に分かってきている。
たしかにニューラルネットは、私たちが「人の手を借りない思考」で容易に気づくような、自然界の規則性に気づくことができる。しかし、数理科学や計算科学の範囲に属することを解明しようとするなら、ニューラルネットにはそれができないだろう–「普通の」計算システムを効果的に「道具として使う」のでなければ。
しかし、これには混乱が生じる可能性がある。過去には、エッセイを書くことも含めて、コンピュータには「根本的に難しすぎる」と思われていた作業がたくさんあった。しかし、ChatGPTのような人がそれをやっているのを見ると、コンピュータはもっと強力になったに違いない、特に、セル・オートマトンのような計算システムの振る舞いを徐々に計算していくようなことは、すでに基本的にできていたことだと思うようになる。
しかし、この結論は正しいとは言えない。たとえコンピュータが個々のステップを容易に計算できたとしても、計算不可能なプロセスは計算不可能なままであり、コンピュータにとって根本的に困難であることに変わりはないのだ。そうではなく、例えばエッセイを書くというような、人間にはできるがコンピュータにはできないと思っていたことが、実はある意味で思ったより計算しやすいという結論になる。
つまり、ニューラルネットがエッセイを書くのに成功するのは、エッセイを書くのが思ったより「計算が浅い」問題であることがわかったからだ。そしてこれは、ある意味で、人間がどのようにしてエッセイを書いたり、一般的に言語を扱ったりしているのかについての「理論」を持つことに近づいている。
十分な大きさのニューラルネットがあれば、人間が容易にできることは何でもできるようになるかもしれない。しかし、自然界一般にできること、あるいは人間が自然界から作り出した道具にできることは、捉えられないだろう。そして、このような道具(実用的、概念的なもの)を使うことで、最近の数世紀で私たちは「純粋な人間の思考」にアクセスできる境界を超え、物理的、計算的宇宙に存在するものを人間の目的のためにより多く取り込むことができるようになったのである。
エンベッディングの概念
ニューラルネットは、少なくとも現在のところ、基本的に数字に基づいている。なので、もしニューラルネットを使ってテキストのようなものを処理しようとするなら、テキストを数字で表現する方法が必要である。確かに(ChatGPTのように)辞書のすべての単語に番号を割り当てることから始めることもできる。しかし、それ以上に重要な考え方(例えばChatGPTの中心的な考え方)がある。それは、「埋め込み」という考え方である。埋め込みとは、「近くにあるもの」は「近くにある数字」で表現される、という性質を持った数字の配列で、何かの「本質」を表現しようとするものだと考えることができる。
例えば、単語の埋め込みは、ある種の「意味空間」に単語を並べ、「意味の近い」単語が埋め込みの中で近くに見えるようにする、と考えることができる。ChatGPTなどで実際に使われている埋め込みは、大きな数字の羅列になりがちである。しかし、2次元に投影すれば、埋め込みによって単語がどのように配置されるかの例を示すことができる。

そして、私たちが見ているものは、典型的な日常の印象を驚くほどよく捉えているのである。しかし、このような埋め込みはどのようにすればできるのだろうか?大まかには、大量のテキスト(ここではWeb上の50億語)を見て、異なる単語が出現する「環境」が「どれだけ似ているか」を見るというものである。例えば、「アリゲーター」と「クロコダイル」は、似たような文章によく出てくるので、埋め込みでは近くに配置されることになる。しかし、”turnip “と”eagle “は、似たような文章にはあまり登場しないので、エンベッディングでは離れた場所に配置されることになる。
しかし、実際にニューラルネットを使ってこのようなことを実現するにはどうしたらよいのだろうか?まずは「言葉」ではなく「画像」のエンベッディングの話からはじめよう。似たような画像には似たような数値のリストを割り当てるというように、画像を数値のリストで特徴付ける方法を考えたいのである。
では、「類似画像とみなす」かどうかは、どのように判断すればよいのだろうか。例えば、手書きの数字の画像であれば、同じ数字の画像であれば「類似している画像とみなす」ことができる。先ほど、手書きの数字を認識するように学習させたニューラルネットを紹介した。このニューラルネットは、最終的な出力において、画像を各桁ごとに10個のビンに分類するように設定されていると考えることができる。
しかし、最終的に「4」であると判断する前に、ニューラルネットの内部で何が起こっているかを「傍受」してみたらどうだろう。ニューラルネットの内部には、「ほとんど4っぽいけど、ちょっと2っぽい」とか、画像を特徴づける数値があると予想される。そして、そのような数字を拾ってきて、埋め込みの要素として使おうということである。
そのコンセプトはこうだ。「どの画像がどの画像の近くにあるのか」を直接的に特徴付けようとするのではなく、明示的な学習データが得られる、明確に定義されたタスク(この場合は数字認識)を考え、このタスクを行う際にニューラルネットが暗黙的に「近さの判断」をしなければならないことを利用するのである。つまり、私たちは「画像の近さ」について明示的に話す必要はなく、ある画像がどの数字を表すかという具体的な問題について話すだけで、それが「画像の近さ」について何を意味するかは「ニューラルネットに任せる」ことになるのである。
では、数字認識ネットワークはどのように機能するのだろうか。このネットワークは11の連続した層から構成されていると考えることができ、それを図式化すると次のようになる(活性化関数は別の層として示される)。
最初の層には実際の画像が入力され、画素値の2次元配列で表現される。これは、ネットワークが、この画像が0から9の各桁に対応していることを「どれだけ確信しているか」を示していると考えることができる。
画像![]() 、その最後の層のニューロンの値をフィードする。
、その最後の層のニューロンの値をフィードする。

つまり、ニューラルネットはこの時点で、この画像が「4」であることを「確信」しており、実際に「4」という出力を得るためには、最大の値を持つニューロンの位置を選び出せばいいだけなのだ。
しかし、もう一歩前に目を向けるとどうだろう。ネットワークの最後の演算は、いわゆるソフトマックスで、「確実性を強制」しようとするものである。しかし、それが適用される前に、ニューロンの値は、次のとおりである。
「4」を表すニューロンは、依然として最も高い数値を持っている。しかし、他のニューロンの値にも情報があるのである。そして、この数字の羅列は、ある意味、画像の「本質」を表すものとして、エンベッディングとして利用できることが期待できる。例えば、「4」は「8」とは微妙に異なる「シグネチャー」(特徴的な埋め込み)を持っているわけである。

ここでは、基本的に10個の数字を使って画像を特徴付けている。しかし、もっと多くの数を使った方が良い場合がある。例えば、数字認識ネットワークでは、前層を叩くことで500個の数字の配列が得られる。そして、これが「画像埋め込み」として使うには妥当な配列だろう。
手書きの数字を「画像空間」として明示的に視覚化するためには、500次元のベクトルを、例えば3次元空間に投影して、「次元を小さくする」必要があるのである。

先程、画像の特徴づけ(ひいては埋め込み)を、学習セットに従って、同じ手書きの数字に対応するかどうかという画像の類似性の識別に効率的に基づいて行うことをお話した。そして、例えば、5000種類の物体(猫、犬、椅子、…)のうち、それぞれの画像がどれに該当するかを特定する学習セットがあれば、同じことを画像に対してもっと一般的に行うことができる。そうすると、一般的な物体を識別することで「固定化」された画像埋め込みが、ニューラルネットの挙動に応じて「汎化」されていくのである。そして、その振る舞いが、私たち人間の画像の捉え方、解釈の仕方と一致する限り、「私たちには正しいと思える」埋め込みになり、実際に「人間の判断に近い」作業をするのに役立つ、というのがポイントである。
では、同じようなアプローチで、単語の埋め込みを見つけるにはどうしたらよいのだろうか?重要なのは、学習が容易な単語に関するタスクから出発することである。そのようなタスクの代表格が「単語予測」である。例えば、「○○な猫」という単語が与えられたとする。大規模なテキストコーパス(例えば、Webのテキストコンテンツ)に基づいて、「空白を埋める」可能性のあるさまざまな単語の確率はどのようなものだろうか?あるいは、「○○黒○○」が与えられた場合、様々な「空白の言葉」の確率はどうだろうか?
この問題をニューラルネットに設定するにはどうしたらいいのだろうか。最終的には、すべてを数字で表現する必要がある。その1つの方法が、5万語ほどある英語の一般的な単語に、それぞれ固有の番号を割り当てることだ。例えば、”the “は914、”cat”(前にスペースを入れて)は3542というように。(つまり、「the ___ cat」問題では、入力は{914, 3542}となる。}出力はどのようなものだろうか?それは、5万個ほどの数字のリストで、「埋め合わせ」の可能性のある単語それぞれの確率を効果的に与えているはずだ。もう一度言うが、埋め込みを見つけるには、ニューラルネットが「結論に達する」直前にその「内部」を「傍受」し、そこで発生する、「それぞれの単語を特徴づける」と考えられる数字のリストを拾えばよいのである。
では、その特徴はどのようなものだろうか。過去10年間に、それぞれ異なるニューラルネットのアプローチに基づくさまざまなシステム(word2vec、GloVe、BERT、GPT、…)が次々と開発されていた。しかし、結局のところ、どのシステムも、単語を取り上げ、数百から数千の数字のリストで特徴付ける。
この「埋め込みベクトル」は、生のままでは、あまり意味のないものである。例えば、GPT-2が生成する3つの単語の埋め込みベクトルは次のようなものである。

このベクトル間の距離を測定するようなことをすれば、単語の「近さ」のようなものがわかる。このような埋め込みの「認知的」な意義については、後ほど詳しく説明する。しかし、今は、言葉を「ニューラルネットに適した」数字の集まりに変える方法がある、ということが重要なのである。
しかし、実際には、単に数字の集まりで単語を特徴づけるだけでなく、単語のシーケンスや、テキストのブロック全体に対して行うことができる。ChatGPTの内部では、そのような処理をしている。そして、これまでに得られたテキストをもとに、それを表現する埋め込みベクトルを生成する。そして、次に出てくる可能性のある単語の確率を求める。そして、その答えを、5万語程度の単語の確率を示す数値の羅列として表現するのである。
(厳密には、ChatGPTは単語を扱わず、むしろ「トークン」-単語全体かもしれないし、「pre」「ing」「ized」などの断片だけかもしれない便利な言語単位を扱う。トークンを使うことで、ChatGPTは珍しい単語や複合語、非英語の単語を扱いやすくなり、時には良くも悪くも新しい単語を作り出すことができる)。
ChatGPT内部
さて、いよいよChatGPTの中身を説明する。そうだ、最終的には巨大なニューラルネットで、現在は1750億の重みを持つGPT-3ネットワークと呼ばれるバージョンになっている。このニューラルネットは、これまで説明してきた他のニューラルネットと多くの点で似ている。しかし、このニューラルネットは、特に言語を扱うために設定されたニューラルネットである。その最大の特徴は「トランスフォーマー」と呼ばれるニューラルネットのアーキテクチャの一部である。
先に述べた最初のニューラルネットでは、任意の層の各ニューロンは基本的にその前の層の各ニューロンと(少なくとも何らかの重みで)接続されていた。しかし、このような完全な連結ネットワークは、特定の既知の構造を持つデータを扱う場合には、(おそらく)過剰な負担となる。そのため、たとえば画像を扱う初期段階では、いわゆる畳み込みニューラルネット(「コンブネット」)を使うのが一般的だ。コンブネットでは、ニューロンを画像のピクセルに似たグリッド上に効果的に配置し、グリッド上の近くのニューロンのみに接続させる。
トランスフォーマーのアイデアは、テキストを構成するトークンのシーケンスに対して、少なくともいくらか似たようなことを行うことである。しかし、単にシーケンスの固定領域を定義して接続するのではなく、トランスフォーマーには「注意」という概念が導入されており、シーケンスのある部分には他の部分よりも「注意」を払うという考え方がある。将来的には、一般的なニューラルネットを起動し、トレーニングによってすべてのカスタマイズを行うことが意味を持つようになるかもしれない。しかし、少なくとも現時点では、変圧器がそうであるように、そしておそらく私たちの脳がそうであるように、物事を「モジュール化」することが実際には重要であるように思われるのである。
では、ChatGPT(というか、そのベースとなったGPT-3ネットワーク)は、実際に何をするのだろうか?ChatGPTの目標は、学習した内容(ウェブ上の何十億ページものテキストを見るなど)に基づいて、テキストを「合理的に」継続することである。
動作は基本的に3段階ある。まず、これまでのテキストに対応するトークンの列を取り出し、それを表す埋め込み(=数値の配列)を見つける。そして、この埋め込みを「標準的なニューラルネットの手法」で操作し、ネットワーク内の連続した層を値が「波打つ」ようにして、新しい埋め込み(=新しい数値の配列)を生成する。そして、この配列の最後の部分を取り出し、そこから約5万個の値の配列を生成する。この値は、次に起こりうるさまざまなトークンの確率に変わる(そう、偶然にも、英語の一般単語とほぼ同じ数のトークンが使われているのだが、トークンのうち約3000だけが単語全体であり、残りは断片なのだ)。
重要なのは、このパイプラインのすべての部分がニューラルネットワークで実装されており、その重みはネットワークのエンドツーエンドの学習によって決定されるという点である。つまり、事実上、全体のアーキテクチャ以外は何も「明示的に設計」されておらず、すべては学習データから「学習」されているだけなのだ。
しかし、アーキテクチャの設定方法には、あらゆる種類の経験とニューラルネットの言い伝えが反映された、たくさんの詳細がある。これは雑草の中に入っていくようなものだが、そのような詳細について話すことは、少なくともChatGPTのようなものを構築するために何が必要かを知るために有用だと考えている。
まずエンベッディングモジュールである。以下はGPT-2のためのWolfram Languageによる模式図である。

入力はn個のトークンからなるベクトル(前節と同じく1から約5万までの整数で表される)である。これらのトークンはそれぞれ、(単層のニューラルネットによって)埋め込みベクトル(長さはGPT-2で768、ChatGPTのGPT-3で12,288)に変換される。一方、トークンの位置の列(整数)を取る「二次経路」があり、この整数から別の埋め込みベクトルが作られる。そして最後に、トークン値とトークン位置の埋め込みベクトルを足し合わせて、埋め込みモジュールからの最終的な埋め込みベクトル列を生成する。
なぜ、token-valueとtoken-positionの埋め込みベクトルを足し合わせるだけなのだろうか?これには特に科学的な根拠はないと思う。ただ、いろいろと試してみた結果、これはうまくいきそうだということである。ニューラルネットは、ある意味で「だいたい正しい」設定であれば、ニューラルネットがどのように構成されているかを「工学レベルで理解」する必要はなく、十分に学習させるだけで細部にこだわることができる、という伝承があるのだ。
以下は、hello hello hello hello hello hello hello hello hello hello hello hello hello hello バイバイ バイバイという文字列を操作するエンベッディングモジュールの動作である。

各トークンの埋め込みベクトルの要素はページの下に表示され、ページをまたぐと、まず「こんにちは」の埋め込みが続き、次に「さようなら」の埋め込みが続いている。上の2番目の配列は位置の埋め込みで、そのややランダムな構造は「たまたま学習された」ものである(この場合はGPT-2で)。
エンベッディングモジュールの後に、トランスフォーマーのメインイベントである「アテンションブロック」(GPT-2は12個、ChatGPTのGPT-3は96個)のシーケンスが来るわけですね。これはかなり複雑で、理解しにくい典型的な大規模工学システム、あるいは生物学的システムを彷彿とさせるものである。とにかく、1つの「アテンションブロック」(GPT-2の場合)の模式図は以下のとおりである。

各注意ブロックの中には、「注意ヘッド」(GPT-2では12個、ChatGPTのGPT-3では96個)があり、それぞれが埋め込みベクトル中の異なる値の塊に対して独立して動作している。(そして、なぜ埋め込みベクトルを分割するのが良いのか、その異なる部分が「何を意味するのか」については、特に理由はなく、ただ「うまくいくことがわかった」ことの一つに過ぎない)。
では、アテンションヘッドは何をするのだろうか?基本的にはトークンの並びを「振り返って」(つまりこれまでに生成されたテキストを)、次のトークンを見つけるのに有効な形で「過去をパッケージ化」する方法である。上記の最初のセクションでは、2-gram確率を使って、直前の単語に基づいて単語を選ぶことについてお話した。つまり、例えば動詞が文中で何語か前に出てくる名詞を参照するようなことが可能になる。
もっと細かく言うと、アテンションヘッドが行うのは、異なるトークンに関連する埋め込みベクトルのチャンクを、ある重みで組み替えることである。そして、例えば、(GPT-2の)最初のアテンションブロックの12個のアテンションヘッドは、上記の「hello,bye」という文字列に対して、以下の(「look-back-all-the-way to-the-beginning of-sequence-of-tokens」)パターンの「再結合重み」を持っている。

アテンション・ヘッドで処理された後、「再重み付けされた埋め込みベクトル」(GPT-2では長さ768、ChatGPTのGPT-3では長さ12,288)は、標準の「完全連結」ニューラルネット層を通される。この層が何をしているのか、把握するのは難しいである。この層が何をしているのか把握するのは難しいのだが、ここでは768×768の重みの行列をプロットしている(GPT-2の場合はこちら)。

64×64の移動平均を取ると、ある種の(ランダムウォーク的な)構造が浮かび上がってくる。

この構造は何によって決定されるのだろうか?最終的には、人間の言語の特徴を「ニューラルネット・エンコーディング」したものと推測される。しかし、今のところ、その特徴が何だろうかは全く分かっていない。つまり、ChatGPT(あるいは少なくともGPT-2)の脳を開いてみると、そこには複雑な構造があり、最終的に人間の言葉を生み出しているにもかかわらず、私たちにはそれが理解できないことがわかる。
つまり、1つのアテンションブロックを通過すると、新しい埋め込みベクトルができ、それがさらにアテンションブロック(GPT-2では12個、GPT-3では96個)を通過していくのである。各アテンションブロックは、「アテンション」と「完全連結」の重みのパターンがそれぞれ決まっている。GPT-2の場合、最初のアテンションヘッドの「hello, bye」入力に対するアテンション重みのシーケンスは以下の通りである。

そして、完全連結層の(移動平均された)「行列」である。

不思議なことに、異なる注意ブロックにおけるこれらの「重みの行列」は非常によく似ているにもかかわらず、重みの大きさの分布は多少異なっていることがある(必ずしもガウス分布とは限らない)。

さて、このような注意のブロックを経て、トランスフォーマーの正味の効果はどうなるのだろうか?基本的には、トークンの列に対する埋め込みのオリジナル・コレクションを、最終的なコレクションに変換することである。そしてChatGPTは、このコレクションから最後の埋め込みをピックアップし、それを「デコード」して、次に来るべきトークンの確率のリストを生成する、という特殊な方法で動作する。
というわけで、ChatGPTの中身を大まかに説明した。一見複雑そうに見えるが(それは多くの必然的でやや恣意的な「工学的選択」のためでもある)、実は関係する究極の要素は驚くほど単純である。なぜなら、最終的に扱うのは「人工ニューロン」でできたニューラルネットであり、それぞれが数値入力の集合を受け取り、ある重みと組み合わせるという単純な操作を行っているだけだからだ。
ChatGPTの入力は数字の配列(これまでのトークンの埋め込みベクトル)で、ChatGPTが新しいトークンを生成するために「実行」することは、これらの数字がニューラルネットの層を「波及」し、それぞれのニューロンが「自分のことをする」ことで次の層のニューロンへ結果を渡すだけなのである。ループもなければ「戻る」こともない。すべてがネットワークを通じて「フィードフォワード」されるだけなのである。
チューリングマシンのように、同じ計算要素によって繰り返し結果が「再処理」されるような一般的な計算システムとは、まったく異なる仕組みになっている。ここでは、少なくとも、与えられた出力のトークンを生成する際に、各計算要素(ニューロンなど)は一度だけ使用される。
しかし、ChatGPTでもある意味、計算要素を再利用する「外側のループ」が残っている。なぜなら、ChatGPTが新しいトークンを生成しようとするとき、ChatGPT自身が以前に「書いた」トークンを含む、それ以前の一連のトークンを常に「読む」(=入力として受け取る)ためだ。つまり、ChatGPTは、少なくとも一番外側のレベルでは、「フィードバック・ループ」をしていると考えることができる。
しかし、ChatGPTの核心である、各トークンを生成するために繰り返し使用されているニューラルネットに話を戻そう。これは非常にシンプルなもので、同一の人工ニューロンの集合体である。このネットワークは、ある層のすべてのニューロンが、その前の層のすべてのニューロンに(ある重みで)接続されている(「完全接続」)ニューロン層で構成されている部分もある。しかし、ChatGPTは特にトランスフォーマーアーキテクチャにより、異なる層の特定のニューロンだけが接続された、より構造的な部分を持っている。(もちろん、「すべてのニューロンがつながっている」とも言えるが、重みがゼロのニューロンもある)。
また、ChatGPTのニューラルネットは、単に「同質な」層で構成されているとは考えにくい側面がある。例えば、上の図にあるように、アテンションブロックの内部では、入力されたデータを「複数コピー」して、それぞれが異なる「処理経路」を通り、異なる数の層を含む可能性があり、後で再結合する場所がある。しかし、これは便利な表現かもしれないが、少なくとも原理的には、層を「密に埋める」ことは常に可能で、ただいくつかの重みをゼロにすることは可能である。
ChatGPTの最長の経路を見ると、約400層(コア層)があり、ある意味大した数ではない。しかし、ニューロンの数は数百万個で、その接続数は1750億、したがって重みも1750億になる。そして、ChatGPTが新しいトークンを生成するたびに、これらの重みの一つ一つを含む計算をしなければならないことを理解する必要がある。これらの計算は、実装的には「層別」に整理して高度に並列な配列演算にすることができ、GPUで便利に実行することができる。しかし、1つのトークンが生成されるごとに、1750億回の計算が行われる(最終的にはもう少し多くなる)。
しかし、結局のところ、これらの操作は、それぞれは単純なものであるにもかかわらず、何らかの形で一緒になって、これほどまでに「人間らしい」テキスト生成の仕事をすることができる、ということが重要なのである。ここでもう一度強調しておかなければならないのは、(少なくとも私たちが知る限り)このような仕組みが機能する「究極の理論的理由」がないことである。実際、これから述べるように、ChatGPTのようなニューラルネットで、人間の脳が言語を生成するのに必要な本質を捉えることができるというのは、科学的に驚くべき発見と言えるのではないだろうか。
ChatGPTのトレーニングについて
さて、ここまででChatGPTの仕組みの概要を説明した。でも、どうやってセットアップしたのだろうか?ニューラルネットの1750億の重みはどのように決定されたのだろうか?基本的には、人間が書いたウェブや書籍などの膨大なテキストコーパスをもとに、非常に大規模な学習を行った結果である。しかし、これだけの学習データがあっても、ニューラルネットが「人間らしい」文章をうまく生成できるかというと、そうとは言い切れない。そしてまた、それを実現するためには、細かなエンジニアリングが必要なようだ。しかし、ChatGPTの大きな驚きと発見は、それがまったく可能であるということである。そして、事実上、1750億個の重みを持つニューラルネットが、人間が書くテキストの「合理的なモデル」を作ることができるということである。
現代では、人間が書いたテキストがデジタル形式でたくさん出回っている。公開されているウェブページには、少なくとも数十億の人間が書いたページがあり、全部で1兆語ものテキストが存在すると思われる。公開されていないウェブページを含めれば、その数は少なくとも100倍以上になるかもしれない。これまでに出版された約1億冊の本のうち、500万冊以上がデジタル化され、さらに約1000億語のテキストが利用可能になっている。個人的な比較だが、私の生涯の出版物は300万語弱で、過去30年間に書いた電子メールは約1,500万語、タイプしたものは全部で5,000万語、ここ数年ではライブストリームで1,000万語以上しゃべっている。そして、そうだ、私はそのすべてからボットを訓練するのである(笑)。
しかし、これだけのデータがあれば、どうやってニューラルネットを学習させるのだろうか?基本的なプロセスは、上記の簡単な例で説明したのとほとんど同じである。一群の例を提示し、その例に対する誤差(「損失」)を最小にするようにネットワークの重みを調整する。誤差から「逆伝播」する際に高価なのは、これを行うたびにネットワークのすべての重みが少なくともほんの少し変化するのが普通で、扱うべき重みの数が多くなってしまうからだ。(実際の「逆計算」は「前進」よりも小さな定数倍だけ大変なのである)。
最新のGPUハードウェアを使えば、何千もの例から得られた結果を並列に計算するのは簡単である。しかし、実際にニューラルネットの重みを更新するとなると、現在の手法では基本的にバッチごとに行う必要がある。(このあたりは、計算とメモリが一体化した実際の脳が、少なくとも今のところはアーキテクチャ的に優位に立っているのだろう)。
先ほどの数値関数の学習という一見シンプルなケースでも、少なくともゼロからネットワークをうまく学習させるためには、数百万件の例を用いなければならないことが多いことがわかった。では、「人間のような言語」モデルを学習させるためには、どれくらいの例数が必要なのだろうか?それを知るための根本的な「理論的」方法はないように思われる。しかし、実際にChatGPTは数千億語のテキストで訓練に成功した。
何度も読み込ませたテキストもあれば、一度だけ読み込ませたテキストもある。しかし、どうにかして、見たテキストから「必要なものを得た」のである。しかし、このように大量のテキストから学習する場合、「うまく学習する」ためにはどれくらいの規模のネットワークが必要なのだろうか。これについても、理論的に説明する方法はまだない。最終的には、後述するように、人間の言語とそれを使って人間が通常話す内容には、ある種の「アルゴリズム的な総量」が存在すると推定されるのである。しかし次の問題は、ニューラルネットがそのアルゴリズム的内容に基づいたモデルをどれだけ効率的に実装できるかということである。ChatGPTの成功は、それが合理的に効率的であることを示唆しているが、私たちにはまだわからない。
そして、ChatGPTは、与えられた学習データの単語(またはトークン)の総数に匹敵する、数千億の重みを使って動作していることに注目すればよい。ChatGPTの小規模な類似品でも経験的に観測されているが、うまく機能する「ネットワークのサイズ」が「学習データのサイズ」に匹敵するのは、ある意味で驚くべきことかもしれない。結局のところ、Webや書籍などのテキストがすべて「ChatGPTの内部」に何らかの形で「直接保存」されているわけではないことは確かだ。なぜなら、ChatGPTの中にあるのは、10桁弱の精度の数字の束であり、それは、すべてのテキストの集合構造をある種の分散エンコーディングで表現したものだからだ。
別の言い方をすれば、人間の言葉の「有効な情報量」とは何か、それで典型的に何が語られているのかを問うことができるかもしれない。そこには生の言語例のコーパスがある。そして、ChatGPTのニューラルネットにおける表現がある。この表現は、(後述するように)「アルゴリズム的に最小の」表現からはほど遠い可能性が高い。しかし、ニューラルネットが容易に利用できる表現である。そして、この表現では、最終的に学習データの「圧縮」はほとんど行われないようだ。基本的に平均して、学習データ1語の「情報量」を運ぶのに必要なニューラルネットのウェイトは1個より少し少ない程度であるようだ。
ChatGPTでテキストを生成する場合、基本的に各ウェイトを1回ずつ使うことになる。そのため、重みがn個ある場合、計算ステップはn回になるが、実際にはGPUで並列処理することができる。しかし、重みを設定するために約n語の学習データが必要だとすると、上で述べたことから、ネットワークの学習を行うには約n2の計算ステップが必要だと結論付けることができる。
ベーシックトレーニングの先にあるもの
ChatGPTの学習は、ウェブや本などの既存のテキストを大量に「見せる」ことに労力を費やしている。しかし、もう一つ、かなり重要な部分があることがわかった。
ChatGPTのニューラルネットは、元となるコーパスのテキストからの「生トレーニング」を終えるとすぐに、プロンプトから続く独自のテキストを生成し始める準備ができている。しかし、その結果は合理的に見えることも多いのだが、特に長いテキストでは、人間離れした「迷走」をしてしまうことがある。これは、例えば従来の統計学的な手法ではなかなか発見できないことである。しかし、実際に文章を読んでいる人間であれば、容易に気づくことなのである。
そして、ChatGPT構築のキーとなるアイデアは、Webなどの「受動的に読む」ことの次のステップとして、実際の人間が積極的にChatGPTと対話し、何を生み出すかを見て、事実上「どうすれば良いチャットボットになるか」をフィードバックさせることだった。しかし、ニューラルネットはそのフィードバックをどのように利用できるのだろうか。最初のステップは、ニューラルネットの結果を人間が評価することだけだ。しかしその後、その評価を予測しようとする別のニューラルネットモデルが構築される。しかし、この予測モデルは、元のネットワーク上で損失関数のように実行することができ、事実上、与えられた人間のフィードバックによってネットワークが「チューニング」されることになる。そして、その結果は、システムが「人間らしい」出力を出すかどうかに大きく影響するようだ。
一般に、「もともと訓練された」ネットワークが、特定の方向に進むために必要な「つつき」がほとんどないのは興味深いことである。ネットワークが「新しいことを学んだ」かのように振る舞うには、学習アルゴリズムを実行し、重みを調整する必要がある、と考える人もいるかもしれない。
しかし、そのようなことはない。むしろ、ChatGPTは基本的にプロンプトの一部として一度だけ何かを伝えれば十分で、あとはテキストを生成するときに伝えたことをうまく利用することができるようだ。このことは、ChatGPTが「何をやっているのか」「人間の言語や思考の構造とどう関係しているのか」を理解する上で、重要な手がかりになると思う。
少なくとも一度、事前学習をしておけば、それを「記憶」することができる。少なくとも、それを使ってテキストを生成するのに十分な時間、記憶することができる。では、このような場合、何が起こっているのだろうか。それは、「伝えるべきことはすでにどこかにあって、それを正しい場所に導いているだけ」ということかもしれない。しかし、それはあまり現実的ではない。それよりも、「要素はすでにあるけれども、その要素間の軌跡のようなものが具体的に定義されていて、それが何かを伝えるときに導入される」という可能性の方が高そうだ。
そして実際、人間と同じように、自分の知っている枠組みにまったく当てはまらない奇抜なことを言っても、うまく「統合」できそうにない。基本的には、すでに持っている枠組みの上に、かなりシンプルな形で乗っている場合にのみ、「統合」することができる。
ニューラルネットが「拾える」ものには、どうしても「アルゴリズム的な限界」があることも改めて指摘しておきたい。「これがこうなる」といった形の「浅い」ルールを与えれば、ニューラルネットはそれをうまく表現・再現できるだろうし、実際に言語から「すでに知っている」ことで、従うべきパターンがすぐに見つかるだろう。しかし、潜在的に計算不可能な多くのステップを含む、実際の「深い」計算のためのルールを与えようとしても、うまくいかない。(各ステップでは、常にネットワークに「データを送り込む」だけで、新しいトークンを生成する以外には決してループしないことを思い出してほしい)。
もちろん、ネットワークは特定の「不可逆的」な計算に対する答えを学習することができる。しかし、可能性が組み合わせ論的に多数存在するようになると、そのような「テーブル・ルックアップ式」のアプローチは通用しなくなる。そう、人間と同じように、ニューラルネットも「手を伸ばして」実際の計算ツールを使うべき時が来たのだ。(そして、Wolfram|AlphaとWolfram Languageは、言語モデルのニューラルネットと同じように「世界の物事について話す」ために作られているので、他に類を見ないほど適している)。
ChatGPTの本当の魅力とは?
人間の言語とその生成に関わる思考プロセスは、常に一種の複雑性の頂点を示しているように思われる。そして実際、1000億個ほどのニューロン(と、おそらく100兆個の接続)からなるネットワークを持つ人間の脳が、それを担うことができるのは、いささか驚くべきことであるように思われてきた。おそらく、脳にはニューロンのネットワーク以上の何かがあり、未知の物理学の新しい層があるのだろうと想像されたかもしれない。しかし今回、ChatGPTによって新たな重要な情報が得られた。それは、脳のニューロンとほぼ同じ数の接続を持つ純粋な人工ニューラルネットワークが、人間の言語を驚くほどうまく生成できることが分かったのである。
神経網の重みは、現在世界で使われているテキストの単語数とほぼ同数だろうから、これはまだ大きく複雑なシステムである。しかし、言語の持つ豊かさと言語が語ることのできる事柄のすべてが、このような有限のシステムに内包されるとは、あるレベルではまだ信じがたいことである。その理由の一つは、(ルール30の例で初めて明らかになった)計算過程が、たとえその基礎となるルールが単純であっても、事実上システムの見かけ上の複雑さを大幅に増幅させるという、どこにでもある現象の反映であることは間違いない。しかし実は、上で述べたように、ChatGPTで使われているようなニューラルネットは、この現象の影響とそれに伴う計算の不可逆性を制限し、より学習しやすいように特別に構成されている傾向がある。
では、なぜChatGPTのようなものが、言語を使ってここまでできるのだろうか。その基本的な答えは、「言語というのは基本的に見た目よりも単純なものだから」だと思う。つまり、ChatGPTは、究極的に単純なニューラルネットの構造であっても、人間の言語とその背後にある思考の「本質を捉える」ことに成功しているのである。そしてさらに、ChatGPTはその訓練の中で、言語(と思考)の規則性を何らかの形で「暗黙のうちに発見」し、それを可能にしているのである。
ChatGPTの成功は、科学の基本的かつ重要な部分を証明していると思う。それは、新しい「言語の法則」、つまり事実上「思考の法則」が発見されることを期待できる、ということである。ChatGPTはニューラルネットとして構築されているため、これらの法則はせいぜい暗黙のうちに存在する程度である。しかし、もし法則を明示することができれば、ChatGPTが行っているようなことを、より直接的、効率的、かつ透明性の高い方法で行える可能性がある。
しかし、では、これらの法律はどのようなものなのだろうか。最終的には、言語とそれを使って言うことがどのように組み合わされるかについて、ある種の処方箋を与えてくれるに違いない。後ほど、「ChatGPTの内側を見る」ことがどのようにこのヒントを与えてくれるのか、また、計算機言語の構築から得られた知見がどのように今後の道筋を示唆しているのかについて説明する。その前に、古くから知られている「言語の法則」とも言える2つの例について、それらがChatGPTの動作とどのように関係しているのかを説明する。
第一は、言語の構文である。言語とは、単に単語をランダムに並べたものではない。例えば、英語では、名詞の前に形容詞、後に動詞を置くことができるが、通常、2つの名詞を隣り合わせに置くことはできない。このような文法構造は、「解析木」のようなものをどのように組み合わせるかを定義するルール群によって、(少なくとも近似的には)捉えることができる。

ChatGPTは、そのようなルールを明示的に「知っている」わけではない。しかし、訓練によって暗黙のうちにそれを「発見」し、それに従うことが得意なようだ。では、その仕組みはどうなっているのだろうか。「大局的」なレベルでは、それは明らかではない。しかし、もっと簡単な例を見てみると、そのことがよくわかるかもしれない。
()と()の並びからなる「言語」で、括弧は常にバランスさせることを指定した文法を、次のような構文木で表現することを考えてみよう。

ニューラルネットを学習させて、「文法的に正しい」括弧の並びを生成することは可能だろうか?ニューラルネットで配列を扱う方法はいろいろあるが、ChatGPTが行っているように、トランスフォーマーネットを使ってみよう。そして、簡単な変換ネットがあれば、文法的に正しい括弧の並びを学習例として与え始めることができる。このとき、「内容トークン」(ここでは「(」と「)」)に加えて、「終了」トークンが必要になる。
もし、8個のヘッドを持つ1個の注意ブロックと長さ128の特徴ベクトル(ChatGPTも長さ128の特徴ベクトルを使うが、それぞれ96個のヘッドを持つ96個の注意ブロック)を持つ変換ネットを設定すると、括弧言語についてあまり学習させることができないように見える。しかし、2つのアテンションヘッドを用いると、少なくとも1000万程度の例を与えると、学習過程が収束するようだ(トランスフォーマーネットによくあることだが、さらに例を与えると性能が低下するようだ)。
このネットワークを使えば、ChatGPTと同じように、次のトークンを括弧で囲んで確率を求めることができるのである。

最初のケースでは、ネットワークは配列がここで終わることはできないと「確信」している。これは良いことで、もし終わると括弧がアンバランスなままになってしまうからだ。しかし、2つ目のケースでは、ネットワークは「正しく認識」しており、「もう一度始める」ことが可能であることを「指摘」している。しかし、おっと、40万回ほど苦労して学習させた重みをもってしても、次のトークンが「)」である確率は15%だと言うのである。
以下は、()の連続が徐々に長くなっていく場合に、最も高い確率で完成するものをネットワークに問い合わせた場合の結果である。

そして、そう、ある長さまではネットワークはうまくいくのである。しかし、その後、失敗し始める。ニューラルネット(あるいは機械学習全般)において、このような「正確な」状況で見られるのは、かなり典型的な種類のものである。人間が「ひと目で解ける」ケースはニューラルネットも解ける。しかし、「よりアルゴリズム的」なこと(例えば、括弧が閉じているかどうかを明示的に数えるなど)をしなければならないケースは、ニューラルネットはなぜか「計算が浅すぎて」確実にできない傾向がある。(ちなみに、現在のChatGPTでも、長い括弧を正しくマッチングするのは困難である)。
では、ChatGPTや英語のような言語の構文にはどのような意味があるのだろうか。括弧の言語は「厳密」であり、より「アルゴリズム的な物語」である。しかし、英語では、局所的な単語の選択やその他のヒントに基づいて、文法的に何が適合するかを「推測」することができる方がはるかに現実的である。ニューラルネットは、人間も見落とすような「形式的に正しい」ケースを見落とす可能性があるにせよ、この点でははるかに優れている。しかし、重要なのは、言語には全体的な構文構造があり、それが意味するあらゆる規則性があるという事実が、ある意味でニューラルネットが「どれだけ」学習しなければならないかを制限しているということである。そして、重要な「自然科学的」観察は、ChatGPTのようなニューラルネットの変換器アーキテクチャは、すべての人間の言語に(少なくともある程度近似的に)存在すると思われる、入れ子構造に似た構文構造をうまく学習できるようだ、ということである。
構文は言語に対する制約の一種を提供する。しかし、それ以上の制約があることは明らかである。例えば、「好奇心旺盛な電子は魚のために青い理論を食べる」という文章は、文法的には正しいのだが、人が通常言うべき言葉ではないし、ChatGPTがこれを生成しても成功とはみなされないだろう。
しかし、文章が意味を持つかどうかを見分ける一般的な方法はあるのだろうか。そのための伝統的な全体論はない。しかし、ChatGPTはウェブなどから数十億の(おそらく意味のある)文章を学習して、暗黙のうちに「そのための理論を開発した」と考えることができるものなのである。
その理論とはどのようなものだろうか。基本的に2千年前から知られている、論理学という小さなコーナーがある。アリストテレスが発見した三段論法では、論理学は基本的に、あるパターンに従った文は合理的であり、そうでない文は合理的でないとするものである。したがって、例えば、「すべてのXはYである。これはYではないのでXではない」(「すべての魚は青である。「これは青ではないので魚ではない」というように)というのは合理的である。そして、アリストテレスがレトリックの例をたくさん見て(「機械学習」的に)三段論法を発見したように、ChatGPTの学習においても、ウェブ上のテキストなどをたくさん見て「三段論法を発見」できただろうと想像することができるのである(そして、そうでありながら、ChatGPTは、「三段論法を発見」することができる)。(そのため、ChatGPTは、三段論法などに基づく「正しい推論」を含むテキストを生成することは期待できるが、より高度な形式論理となると話は全く別で、括弧合わせで失敗するのと同じような理由でここで失敗することが予想されると思う)。
しかし、論理という狭い例を超えて、もっともらしい意味のあるテキストを体系的に構築する(あるいは認識する)方法について、何が言えるだろうか。確かに、マッド・リブのように、非常に特殊な「句のテンプレート」を使うものはある。しかし、ChatGPTはもっと一般的な方法を暗黙のうちに持っている。そして、その方法については、「1750億個のニューラルネットの重みがあれば、どうにかなる」という以上のことは、おそらく何もないのだろう。でも、もっとシンプルで強い話があるのではないかと強く思っている。
意味空間と意味運動の法則
ChatGPTの内部では、どんなテキストも、ある種の「言語特徴空間」の点の座標と考えることができる数値の配列で効果的に表現されていることを上で説明した。つまり、ChatGPTがテキストを続けることは、言語特徴空間における軌跡をたどることに相当するのである。しかし、この軌跡を意味あるテキストに対応させるのは何なのか、考えることができるようになった。そして、言語特徴空間内の点が「意味」を保ちながら移動する方法を定義する、あるいは少なくとも制約する「意味運動法則」のようなものが、もしかしたら存在するかもしれないのである。
では、この言語特徴空間はどのようなものだろうか。このような特徴空間を2次元に投影すると、1つの単語(ここでは普通名詞)がどのようにレイアウトされるのか、例を挙げてみよう。

前述では、植物と動物を表す単語をベースにした別の例を見た。しかし、いずれの場合も「意味的に近い言葉」が近くに配置されていることがポイントである。
例えば、品詞に対応する単語を並べるとこうなる。

もちろん、ある単語が「一つの意味」を持つとは限らない(また、必ずしも一つの品詞に対応するとは限らない)。また、ある単語を含む文がどのように特徴空間に配置されるかを見ることで、「クレーン」という単語(鳥か機械か)の例のように、異なる意味を「切り分ける」ことができる場合もある。

なるほど、この特徴空間には「意味の近い単語」が近くに配置されていると考えるのが少なくとも妥当であろう。しかし、この空間にはどのような付加的な構造が確認できるのだろうか。例えば、空間に「平坦さ」を反映するような「平行移動」の概念のようなものはあるのだろうか。それを知るための一つの方法は、アナロジーを見ることである。

そうそう、2Dに投影したときでも、確かに万能ではないのだが、少なくとも「平坦さのヒント」があることが多いのである。
では、軌跡はどうだろうか。ChatGPTのプロンプトが特徴空間で辿る軌跡を見ることができ、さらにChatGPTがそれをどのように引き継いでいるかを見ることができる。

確かにここには、「幾何学的に明らかな」運動法則はない。そして、それは全く驚くべきことではなく、これはかなり複雑な話であることが十分に予想される。また、例えば、「意味論的な運動法則」が見つかったとしても、それがどのような埋め込み(実質的にはどのような「変数」)で記述されるのが最も自然なのか、自明とは言い難い。
上の図では、ChatGPTが最も確率の高い単語を選んでいる「軌跡」のいくつかのステップを示している(「温度ゼロ」の場合)。しかし、ある時点でどのような単語がどのような確率で「次に来る」可能性があるのかを問うこともできる。

そして、この場合、高確率の単語の「扇形」が特徴空間に多かれ少なかれ決まった方向に向かっているように見える。さらに進むとどうなるのだろうか。軌跡に「沿って」進むと、次のような「扇形」が現れる。

合計40ステップを目指す、3D表現がこちら。

そして、ChatGPTが内部で何をしているか」を経験的に研究することによって、「数学物理学的な」「意味的な運動法則」を特定することが期待できるという考えを特に後押しするものではないように思える。しかし、もしかしたら私たちは「間違った変数」(あるいは間違った座標系)を見ているだけで、正しい変数さえ見ていれば、ChatGPTが測地線をたどるような「数学物理学的に単純な」ことをしていることがすぐに分かるかもしれない。しかし、今のところ、ChatGPTが人間の言語の「組み立て方」について「発見」したことを、その「内部動作」から「経験的に解読」することはできていない。
意味文法と計算言語の力
「意味のある人間の言葉」を生み出すには、何が必要なのだろうか。かつては、それは人間の脳でなければできないことだと考えていたかもしれない。しかし、今ではChatGPTのニューラルネットでかなり立派なものができることが分かっている。でも、もしかしたらそれが限界で、もっと単純で、もっと人間にわかりやすいものはないかもしれない。しかし、私の強い疑念は、ChatGPTの成功によって、重要な「科学的」事実が暗黙のうちに明らかになったことである。それは、意味のある人間の言語には、実はこれまで知られていたよりもずっと多くの構造と単純さがあり、最終的には、そうした言語を組み立てる方法を示すかなり単純なルールさえ存在するのではないかということである。
先に述べたように、構文文法は、人間の言葉の中で、品詞の違いなどに対応する単語をどのように組み合わせたらよいかというルールを与えるものである。しかし、意味を扱うには、もっと踏み込む必要がある。そのためには、言語の統語的な文法だけでなく、意味的な文法も考えることが一つの方法である。
構文の目的には、名詞や動詞のようなものを識別する。しかし、意味論のためには、「より細かいグラデーション」が必要である。例えば、「移動する」という概念と、「場所に依存せず同一性を保つ」「物体」という概念を識別することができるわけである。このような「意味概念」の具体例はそれぞれ無限にある。しかし、意味文法の目的には、基本的に「物」は「動く」ことができるという一般的なルールのようなものを用意すればいいのである。このような文法がどのように機能するかについては、いろいろと説明することができる(以前にも説明したことがある)。しかし、ここでは、前進する可能性のある道筋を示すいくつかの発言で満足することにする。
なお、意味文法上は全く問題ない文であっても、それが実際に実現された(あるいは実現しうる)とは限らない。「象が月に行った」という文は、意味文法には間違いなく「合格」だが、実際の世界では(少なくともまだ)実現されていないことは確かである。
「意味文法」について語り始めると、すぐに「その根底には何があるのか?」という問いに導かれる。それはどんな「世界のモデル」を想定しているのか?構文文法は、言葉から言語を構築することだけを目的とした文法である。しかし、意味文法は、必然的に何らかの「世界のモデル」、つまり、実際の言葉から作られた言語を重ねるための「骨格」のようなものに関わる。
近年まで、私たちは(人間の)言語が「世界のモデル」を記述する唯一の一般的な方法であると想像していたかもしれない。すでに数世紀前から、特に数学に基づいて、特定の種類の物事を形式化することが行われるようになっていた。しかし、現在では、より一般的な形式化のアプローチとして、計算機言語がある。
そう、これが40年以上にわたる私の大きなプロジェクトだった(現在はWolfram Languageで具体化されている).例えば、都市や分子,画像,ニューラルネットワークの記号表現があり、それらの計算方法に関する知識も組み込まれている。
そして、何十年もかけて、こうして多くの分野をカバーしていた。しかし、これまで私たちは特に「日常的な談話」を扱ってかなかった。私は2ポンドのリンゴを買った」では、「2ポンドのリンゴ」を容易に表現できる(そして栄養計算などもできる)。しかし、「買った」を表す記号表現は(まだ)ない。
この文法は、概念のための一般的な記号の「組み立てキット」であり、何が何と組み合わされるのか、つまり、人間の言語になるまでの「流れ」のルールを与えるという目標につながる。
しかし、この「象徴的な談話言語」を手に入れたとしよう。それを使って何をするのだろうか。まずは「局所的に意味のあるテキスト」を生成するようなことができるだろう。しかし、最終的には、より「グローバルに意味のある」結果、つまり、世界(あるいは、ある一貫したフィクションの世界)に実際に存在しうるもの、起こりうることについて、より「計算」することが必要になるだろう。
現在Wolfram Languageには、様々な種類のものごとに関する膨大な計算知識が組み込まれている。しかし、完全な記号的談話言語とするためには、世界の一般的な事柄に関する「計算」を追加しなければならないだろう.
記号的な談話言語があれば、それを使って「独立した文」を作ることができるかもしれない.しかし、「Wolfram|Alphaスタイル」で世界について質問するために使うこともできる。また、「そうしたい」ことを、おそらくは何らかの外部作動機構を用いて述べるのにも使える。また、実際の世界について、あるいは架空のものであれ何であれ、私たちが考えている特定の世界について、アサーションを行うために使うこともできます。
人間の言葉は基本的に不正確である。特に、特定の計算機実装に「縛られて」いないため、その意味は基本的にそのユーザーの間の「社会契約」によってのみ定義される。しかし、計算言語はその性質上、ある種の基本的な正確さを備えている。なぜなら、計算言語で指定されたものは最終的に必ず「コンピュータ上で一義的に実行」される可能性があるからだ。人間の言葉には、ある種の曖昧さがつきまといる。(しかし、計算機言語では、すべての区別を正確に、明確にしなければならないのである。
計算言語で名前を作るとき、普通の人間の言葉を利用すると便利なことが多い。しかし、計算言語での意味は必ずしも正確ではなく、一般的な人間の言語での特定の意味合いをカバーしているかどうかはわからない。
一般的な記号的談話言語に適した基本的な「存在論」は、どのように考えればいいのだろうか。それは簡単なことではない。だからこそ、アリストテレスが二千年以上前に始めた原初的なものから、この分野ではほとんど何も行われてこなかったのであろう。しかし、今日、私たちは計算機的に世界を考える方法について多くのことを知っているので、本当に助かる(私たちの物理学プロジェクトとルリアッドの考えから「基本的な形而上学」を持っていることも悪くない)。
しかし、ChatGPTの文脈ではどうなのだろうか?ChatGPTは、その訓練から、ある種の(かなり印象的な)量の意味文法を効果的に「つなぎ合わせて」きた。しかし、その成功は、より完全なものを計算言語形式で構築することが可能であろうという根拠を与えてくれる。そして、ChatGPTの内部についてこれまで解明されたこととは異なり、人間が容易に理解できるような計算言語を設計することが期待できる。
意味文法について語るとき、音素論理学とのアナロジーを描くことができる。当初は、人間の言葉で表現された文に関するルールの集合体であった「音素論理」しかし(そう、2千年後に)形式論理が開発されると、もともとの対句論理の基本構成を使って、例えば現代のデジタル回路の動作を含む巨大な「形式の塔」を構築することができるようになったのだ。そして、より一般的な意味文法もそうなることが予想される。最初は、例えばテキストで表現されるような単純なパターンを扱えるだけかもしれない。しかし、ひとたび計算言語のフレームワーク全体が構築されれば、「一般化意味論理」の高い塔を建てることができるようになり、これまで曖昧なまま人間の言語を通じて「床上レベル」でしかアクセスできなかったあらゆる種類のものを、正確かつ形式的に扱うことができるようになると予想される。
計算言語や意味文法の構築は、物事を表現する上での一種の究極の圧縮を意味すると考えることができる。なぜなら、例えば、普通の人間の言語に存在する「言い回し」をすべて扱わなくても、可能なことの本質について話すことができるからだ。そして、ChatGPTの大きな強みも、これと少し似たようなものだと捉えることができる。なぜなら、これもある意味で「ドリルスルー」して、さまざまな言い回しの可能性を気にせずに「意味的に意味のある形で言語をまとめられる」ところまで到達しているからだ。
では、ChatGPTを基礎となる計算言語に適用したらどうなるだろうか。計算言語は、何が可能かを記述することができる。しかし、「何が流行っているか」という感覚は、例えばウェブ上のあらゆるコンテンツを読むことによって、まだ追加することができる。しかし、計算言語を使って操作するということは、ChatGPTのようなものが、潜在的に還元不可能な計算を利用するための究極のツールに即時かつ根本的にアクセスすることを意味する。そして、このシステムは「妥当なテキストを生成する」だけでなく、そのテキストが世界について、あるいはそのテキストが語るべきことについて、実際に「正しい」発言をしているかどうかについて、解決できることを期待できるシステムなのである。
ChatGPTは何をやっているのか、そしてなぜうまくいくのか?
ChatGPTの基本的なコンセプトは、ある意味とてもシンプルである。ウェブや書籍などから、人間が作成した膨大なテキストサンプルからスタートする。そして、ニューラルネットを学習させ、「こんな感じのテキスト」を生成させる。特に、「プロンプト」から始めて、「学習させたものと同じような」テキストを続けることができるようにする。
これまで見てきたように、ChatGPTの実際のニューラルネットは非常にシンプルな要素で構成されている(ただし、その数は数十億個)。そしてニューラルネットの基本的な動作も非常にシンプルで、新しい単語(または単語の一部)を生成するたびに、これまでに生成したテキストから得た入力を「一度だけ」(ループなどを使わずに)要素に通すだけだ。
しかし、驚くべきこと、そして予想外のことは、このプロセスによって、ウェブや本などにあるものとうまく「似た」テキストを作り出すことができるということである。そして、それは首尾一貫した人間の言語であるだけでなく、「読んだ」内容を利用して「その促成に従った」ことを「言う」のである。なぜなら、(例えばWolfram|Alphaの「計算超能力」にアクセスしなければ)学習教材で「どのように聞こえるか」に基づいて「正しく聞こえる」ことを言うだけだからだ。
ChatGPTの具体的なエンジニアリングは、かなり説得力のあるものになっている。しかし、最終的には(少なくとも外部ツールを使えるようになるまでは)ChatGPTは蓄積した「常識の統計」から「まとまった文章の糸」を引き出している「だけ」である。しかし、その結果がいかに人間らしいものだろうかは驚くべきことである。そして、これまで述べてきたように、これは少なくとも科学的に非常に重要なことを示唆している。人間の言語(とその背後にある思考パターン)は、私たちが考えているよりも、どこか単純で「法則的」な構造を持っているということである。ChatGPTは暗黙のうちにそれを発見している。しかし、意味文法や計算言語などを使って、それを明示的に明らかにすることができる可能性がある。
ChatGPTが行うテキスト生成は非常に印象的で、その結果は通常、私たち人間が生成するものと非常によく似ている。では、ChatGPTは脳のような働きをしているのだろうか?ChatGPTの人工神経網の構造は、最終的に脳を理想化したものである。そして、私たち人間が言語を生成するときに起こっていることの多くの側面が、非常によく似ている可能性が高いと思われる。
トレーニング(学習)に関しては、脳と現在のコンピュータの「ハードウェア」が異なるため、ChatGPTは脳とは異なる(そしてある意味でははるかに効率の悪い)戦略を使わざるを得ない。さらに、一般的なアルゴリズム計算とは異なり、ChatGPTは内部で「ループを持つ」「データに対して再計算を行う」ことがない。そのため、必然的に計算能力が制限される。現在のコンピュータに対してもそうだが、脳に対してもそうだ。
それを「修正」して、なおかつ合理的な効率でシステムを訓練する能力を維持する方法は明らかではない。しかし、そうすることで、将来のChatGPTはさらに「脳的なこと」ができるようになると思われる。もちろん、脳が苦手とすることはたくさんある。特に、不可逆的な計算が必要な場合である。そのためには、脳もChatGPTもWolfram Languageのような「外部ツール」を求めなければならない。
しかし、今のところ、ChatGPTがすでにできるようになったことを見るのはエキサイティングなことである。あるレベルでは、多数の単純な計算要素が予想外の驚くべきことを行うことができるという基本的な科学的事実の素晴らしい例である。また、人間の言語とその背後にある思考のプロセスという人間の条件の中心的な特徴について、その基本的な性質と原理をよりよく理解するための、この2千年間で最高の推進力を与えてくれるものでもある。
感謝
ニューラルネットの開発を始めてから約43年になるが、その間、ニューラルネットについて多くの人と交流していた。その中には、昔からの人、最近になってからの人、そして何年にもわたっての人がいる。Giulio Alessandrini, Dario Amodei, Etienne Bernard, Taliesin Beynon, Sebastian Bodenstein, Greg Brockman, Jack Cowan, Pedro Domingos, Jesse Galef, Roger Germundsson, Robert Hecht-Nielsen, Geoff Hinton, John Hopfield, Yann LeCun, Jerry Lettvin, Jerome LeCun, Jenri R. Bodenste, Jenri R. Bodenste, Jenri R. Bodenste, John Hopfield, Jenri R. Bodenste, Jenri L,Jerry Lettvin, Jerome Louradour, Marvin Minsky, Eric Mjolsness, Cayden Pierce, Tomaso Poggio, Matteo Salvarezza, Terry Sejnowski, Oliver Selfridge, Gordon Shaw, Jonas Sjöberg, Ilya Sutskever, Gerry Tesauro and Timothee Verdier. この作品に協力してくれた、Giulio AlessandriniとBrad Kleeに特に感謝したい。